如果一個項目的核心不是分類準確率,而是概率估計的質量。換句話説,需要的是一個校準良好的模型。這裏校準的定義是:如果模型給一批樣本都預測了25%的正例概率,那這批樣本中實際的正例比例應該接近25%。這就是校準。
解決這個校準問題單看ROC-AUC不夠,要用Brier score或者Log-loss來保證校準質量。
我們先介紹一下我們一般使用的的幾個指標:
ROC-AUC衡量的是模型區分正負樣本的排序能力,跟預測概率的絕對值無關。
Brier score本質上就是預測概率的均方誤差:
brier_score=np.mean((y_proba-y_true) **2)Log-loss則是從似然的角度評估概率質量:
log_loss=-np.mean(y_true*np.log(y_proba) + (1-y_true) *np.log(1-y_proba))這裏用PyCaret的Bank數據集做演示:隨機抽取100組不同的特徵子集,每組特徵分別訓練4種模型(Logistic Regression、Decision Tree、Random Forest、LightGBM),得到400個候選模型。所有指標都在獨立的測試集上計算。
校準圖的可視化邏輯
評估校準最直觀的方式是畫校準圖。方法是把預測概率分成若干區間,每個區間內比較平均預測概率(x軸)和實際正例比例(y軸)。
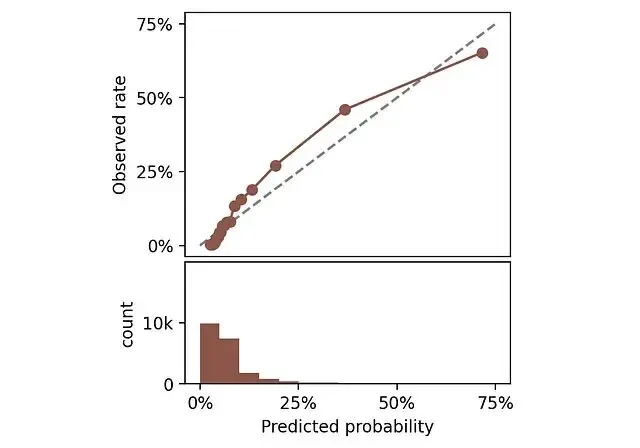
隨機挑一個模型,看看它的校準圖長什麼樣。下面同時畫出預測概率的分佈直方圖。
頂部:校準圖。底部:預測概率直方圖。
完美校準的模型,曲線應該貼着45度對角線。比如某個區間平均預測概率是25%,那這個區間裏實際正例比例也該是25%。曲線偏離對角線越遠説明校準越差。
ECE:從校準圖衍生的量化指標
光看圖不夠還需要一個數值指標。Expected Calibration Error (ECE) 正是從校準圖直接推導出來的。
ECE衡量的就是校準曲線上各點偏離45度線的程度。
假設有這些量:
proba_means:各區間的平均預測概率y_means:各區間的實際正例比例counts:各區間的樣本數
ECE的計算就是加權平均的絕對偏差:
ece=np.sum(np.abs((proba_means-y_means) *counts)) /np.sum(counts)ECE的優點是概念清晰,可以直接測量校準誤差。不像Brier score或Log-loss它們在評估校準的同時還混雜了其他因素。而且ECE沒有對數沒有平方,就是絕對誤差的平均。
既然主要關心校準,那能不能直接用ECE來選模型,不看其他指標?
ECE的侷限性
把400個模型按ECE排序,最小的那個ECE只有0.21%,看起來完美。但是看其他指標就不對了。ROC-AUC只有54%,這基本上是等於隨機猜測。
這就很奇怪了,怎麼會出現校準極好(ECE 0.21%)但排序能力極差(ROC-AUC 54%)的模型?
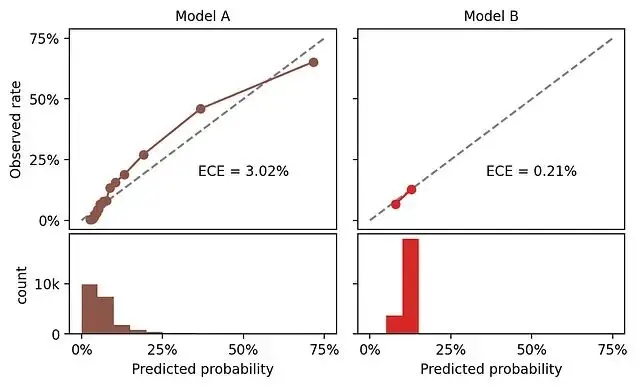
把這個模型(記為Model B)的校準圖跟前面那個模型(Model A)對比一下。
Model B的校準接近完美,原因是它給幾乎所有樣本預測了相同的概率。實際上就是在重複數據集的基準率。
如果數據集10%是正例,一個永遠預測10%的模型當然是完美校準的。但是這個模型沒有卵用,因為它根本區分不了不同的樣本。
所以問題清楚了,需要模型同時滿足兩點:
- 概率校準準確
- 概率有區分度
ECE能評估第一點,但會完全忽略了第二點,所以這時就需要補充一個衡量概率區分度的指標。
pMAD:概率多樣性的度量
有用的模型必須輸出多樣化的概率。Mean Absolute Deviation (MAD) 可以量化這種多樣性,它是各樣本預測概率相對均值的平均偏差:
mad=np.mean(np.abs(y_proba-np.mean(y_proba))這個指標只依賴預測概率本身,跟真實標籤無關所以記為pMAD。
雖然也可以用標準差,但pMAD跟ECE在概念上更一致,因為都是基於絕對差異,便於對比。
現在用ECE和pMAD同時評估Model A和Model B:
Model A和Model B的校準圖對比,包含ECE和pMA,這下就合理了。
Model B確實比Model A校準得更好,但代價是預測概率幾乎沒有區分度:pMAD只有1.4%,而Model A是9.5%。
兩個模型各有問題:
- Model A 校準不足
- Model B 區分度不足
那如何在需要在校準和區分度之間找到平衡點呢?
ECE-pMAD二維評估空間
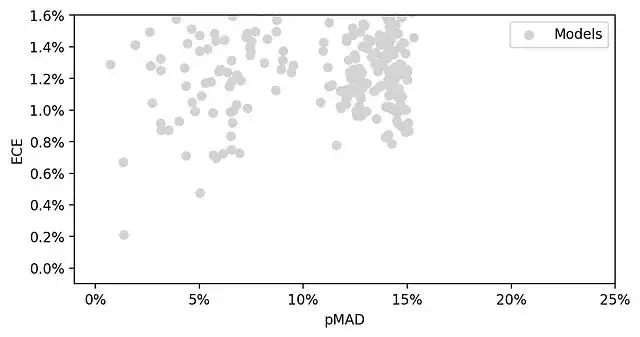
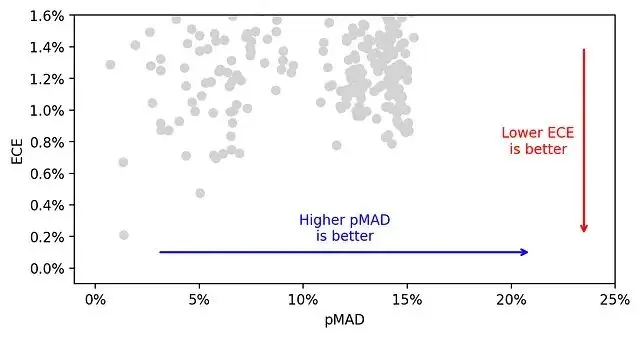
用散點圖展示400個模型在ECE和pMAD兩個維度上的分佈。
理想的模型應該是低ECE、高pMAD,也就是圖的右下角區域。
兩個指標比一個好,但也帶來新問題:更沒法簡單地給模型排序了。這時候就需要引入另外一個概念帕累託前沿。
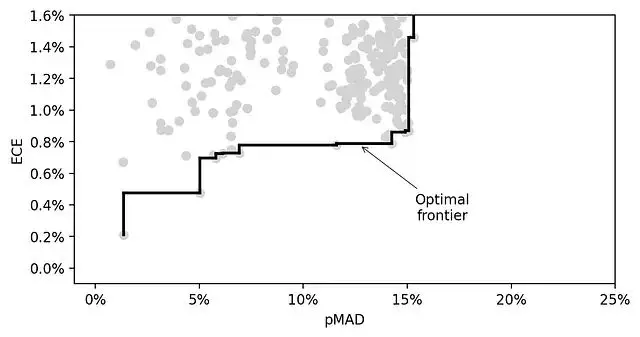
帕累托最優前沿
最優前沿(optimal frontier)定義為:在這條線上的模型,不存在其他模型同時擁有更低的ECE和不低於它的pMAD。
400個模型中只有14個在前沿上,其餘386個都被被其他支配了。
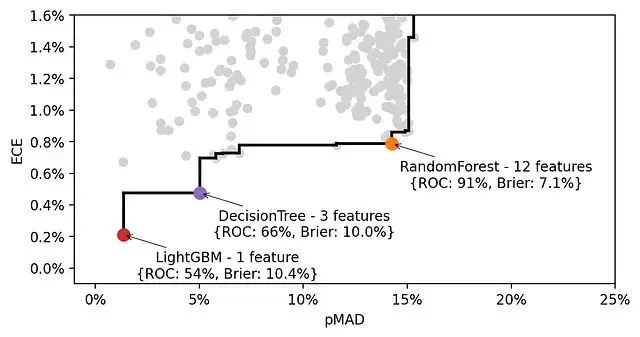
前沿模型的特徵分析
我們在前沿上挑3個模型看看:
這裏就發現了一個有個有意思的規律:特徵數量越多,pMAD越高。這符合我們的理解,更多特徵意味着更多區分樣本的依據。但問題是pMAD增加往往伴隨着ECE的上升,也就是校準變差。
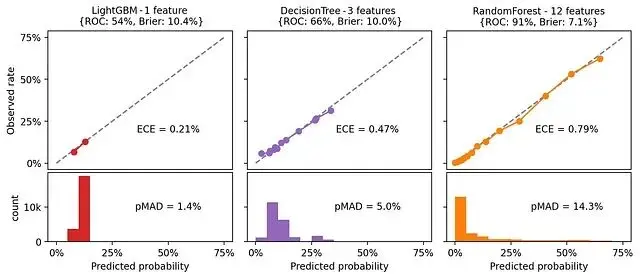
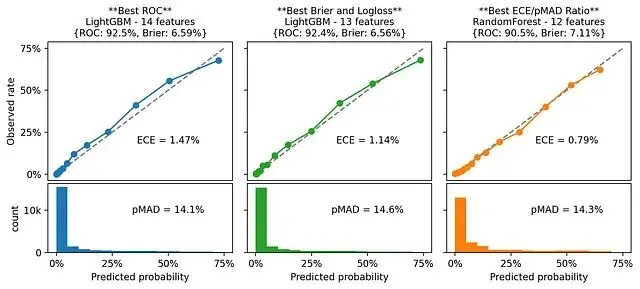
看看這3個模型的校準圖就能理解原因:
概率分佈越分散,ECE就容易增大。但是其實這不代表模型校準真的很差,而是評估方式的問題。
ECE/pMAD比值:綜合評估指標
既然目標是低ECE和高pMAD,一個非常自然的想法是看ECE/pMAD比值。這個比值可以理解為"每單位區分度付出的校準誤差代價"。我們需要要最小化的應該是這個比值而不是原始ECE。
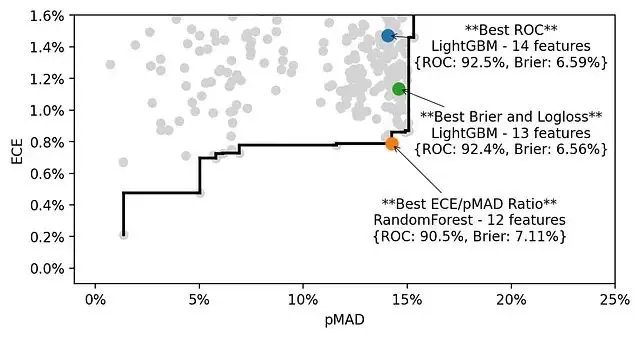
所以可以按以下三種策略各選一個最優模型:
- "最佳ROC":ROC-AUC最高的模型
- "最佳Brier":Brier score和Log-loss最低的模型(在本例中二者一致)
- "最佳ECE/pMAD":ECE/pMAD比值最低的模型
三個模型的pMAD相近,但ECE差異明顯。而且從12個特徵增加到14個,ROC-AUC提升了,但校準變差了。
個人判斷是犧牲少量特徵換取更穩定的概率估計是值得的。
對比ROC-AUC的話最佳校準模型(ECE/pMAD最優)達到90.5%,而ROC最優的也就92.5%。為了校準質量放棄這點ROC是完全可以接受的。
通過校準圖一對比就很清楚了,ECE/pMAD最優的模型(第三個)校準質量明顯更好。這裏用ECE/pMAD比值來篩選,但不是所有情況都適用。另外一種思路是先設定pMAD的最低閾值(比如這個例子裏可以定13%或14%),然後在滿足閾值的模型裏選ECE最小的。
總結
模型概率的可靠性在很多實際場景中至關重要,尤其是當預測結果會影響決策時。ROC-AUC只能評估排序能力,評估校準需要用ECE。但是單用ECE還不夠,因為它無法區分"真校準"和"無區分度"。所以需要同時跟蹤pMAD來評估概率的多樣性。
最優模型應該在校準和區分度之間取得平衡。可以考慮用ECE/pMAD比值,或者先設定pMAD下限再優化ECE。具體用哪種策略,取決於業務場景對這兩個維度的實際需求。
本文的完整代碼:
https://avoid.overfit.cn/post/5a1fb11ae77b480cb2b5a814684e3330
作者:Samuele Mazzanti