傳感器監控、安全運營、欺詐檢測——這些場景都需要及時發現異常狀況。但是問題在於,異常樣本出現頻率低導致標註數據稀缺,監督學習模型難以構建。雖然異常(anomaly)和新穎性(novelty)這兩個概念經常混用,但它們在建模假設和處理流程上存在本質差異。
本文會先講清楚異常檢測的核心概念,分析anomaly和novelty的區別,然後通過實際案例演示如何用概率密度擬合方法構建單變量數據集的無監督異常檢測模型。所有代碼基於distfit庫實現。
Anomaly還是Novelty?差異在哪
兩者都是偏離"常態"的觀測值,統稱為離羣值(outlier)。離羣值通常出現在分佈的尾部,遠離主體密度區域。如果某個值或某個小範圍內出現顯著的密度尖峯,也可能是潛在離羣點。雖然檢測目標一致,建模思路卻不同:
Anomaly(異常):訓練數據中已知存在離羣值,它們偏離正常模式。建模策略是在正常樣本(inlier)上擬合模型,忽略那些偏離樣本,把落在正常行為範圍外的觀測識別為異常。
Novelty(新穎性):訓練數據中不存在已知離羣值,數據本身不包含偏離正常的觀測。這種情況更棘手,因為缺少離羣參照。領域知識在這裏變得關鍵,避免模型在正常樣本上過擬合。
三類離羣值形態
剛才説了anomaly和novelty的建模差異,在建模前需要明確"在具體應用場景下,離羣值長什麼樣"。離羣值大致分三類(圖1):
全局離羣值(point outliers)指那些獨立的、與所有其他觀測都不同的單個數據點[1, 2]。平時説的"離羣值"通常就是指這類。
上下文離羣值(contextual outliers)是在特定上下文下不合理的觀測。上下文可能體現為雙峯或多峯分佈,離羣值在某個峯的範圍內偏離。比如冬天零度以下正常,夏天就成了異常。時間序列、季節性數據、傳感器數據、安全監控都會遇到這類問題。
集體離羣值(collective outliers)是一組相似實例表現出的異常行為。這組離羣點可能形成獨立的峯,往往暗示着不同於單點異常的問題——批處理錯誤或數據生成過程的系統性問題。檢測集體離羣值通常需要專門的方法。
圖1. 從左到右:全局離羣值、上下文離羣值、集體離羣值示例
建模前還要考慮數據集維度。從特徵數量看,異常檢測分為單變量(univariate)和多變量(multivariate)兩種方式。下一節我們詳細講。
單變量 vs 多變量建模
異常檢測的建模路徑主要有兩條:單變量分析和多變量分析(圖2)。本文聚焦單變量隨機變量的異常檢測,先説説區別:
單變量方法每次只用一個變量來判斷樣本是否異常——人的年齡、體重,或時間序列裏的單個變量。這種情況下分析數據分佈很適合做異常檢測。
多變量方法同時分析多個特徵,比如年齡、體重、身高一起看。當特徵間存在(非)線性關係,或各變量分佈嚴重偏斜時,多變量方法更合適。單變量方法在這些場景下效果有限,因為沒考慮變量間的關聯。主成分分析(PCA)就是常用的多變量異常檢測手段。
圖2. 單變量與多變量分析用於異常檢測的對比
用分佈擬合做單變量離羣值檢測
單變量數據集的離羣值檢測有很多(非)參數方法,比如Z-score、Tukey's fences、基於密度的方法等。這些方法的共同點是對底層分佈建模。distfit庫正好擅長這個——既能為單變量隨機變量確定概率密度函數(PDF),也能用百分位數或分位數做非參數建模。它可以處理前面提到的三類離羣值:全局、上下文、集體離羣值。
建模流程大致如下:
- 在多個PDF上計算隨機變量的擬合效果,用擬合優度檢驗對PDF排序,bootstrap驗證是否過擬合。非參數方法也可以用分位數或百分位數實現。
- 可視化檢查直方圖、PDF、CDF和QQ圖。
- 綜合前兩步選最佳模型,但要確保模型特性符合應用場景。選模型不只是統計問題,也是建模決策。
- 用選定的模型對新樣本做預測。
連續隨機變量的Novelty檢測
從一個簡單例子入手,演示如何用分佈擬合和假設檢驗做單變量的novelty檢測。這個例子的目標是開發一種檢測全局離羣值的方法,識別那些偏離正常值的數據點。某個時候需要結合領域知識來設定離羣值的邊界。
下面生成10,000個人類身高測量值,均值163,標準差10。預期是鐘形曲線,兩端分別是偏矮和偏高的樣本。注意隨機性可能讓重複實驗的結果略有差異。
# import library
import numpy as np
# Generate 10000 samples from a normal distribution
X = np.random.normal(163, 10, 10000)1、找出最適合人類身高的PDF
檢測異常前先要對"正常身高"擬合一個分佈(PDF)。distfit庫可以擬合多達89個理論分佈,這裏只搜索常見的概率密度函數,因為身高數據大概率是鐘形曲線。安裝依賴
# Install distfit library
pip install distfit代碼:
# import library
from distfit import distfit
# Initialize for common/popular distributions with bootstrapping.
dfit = distfit(distr='popular', n_boots=100)
# Estimate the best fit
results = dfit.fit_transform(X)
# Plot the RSS and bootstrap results for the top scoring PDFs
dfit.plot_summary(n_top=10)
# Show the plot
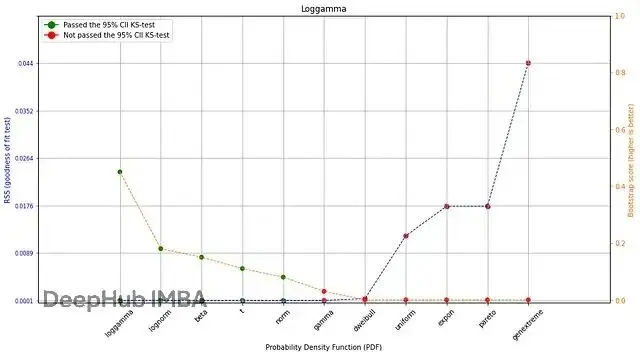
plt.show()圖3. 最常見分佈擬合人類身高的RSS得分
根據擬合優度統計量(RSS)和bootstrap驗證,loggamma PDF是人類身高的最佳擬合。bootstrap方法評估PDF有沒有過擬合,得分在[0,1]區間,反映在100次bootstrap中的擬合成功率。從圖3看,除了loggamma,還有其他幾個RSS較低的PDF——Beta、Gamma、Normal、t分佈、廣義極值、Weibull分佈。但只有五個通過了bootstrap檢驗(圖3中的綠點)。
2、可視化檢驗最佳擬合
目測擬合效果,可以讓我們更加確定選擇,distfit庫提供了繪圖功能,可以畫直方圖配合PDF/CDF,還有QQ圖。
# Make figure
fig, ax = plt.subplots(1, 2, figsize=(20, 8))
# PDF for only the best fit
dfit.plot(chart='PDF', n_top=1, ax=ax[0]);
# CDF for the top 10 fits
dfit.plot(chart='CDF', n_top=10, ax=ax[1])
# Show the plot
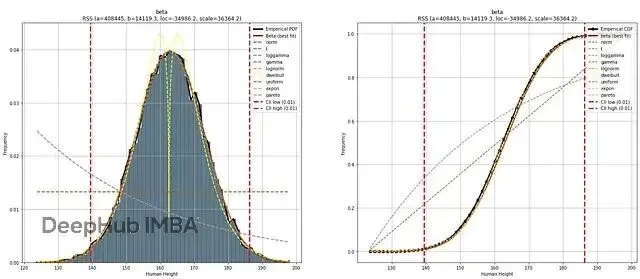
plt.show()圖4. 帕累託圖:經驗數據直方圖和估計PDF。左圖:最佳擬合(Beta)的PDF;右圖:前10個擬合的CDF。置信區間alpha=0.05
可視化驗證了top PDF的擬合優度得分。不過Weibull分佈(圖4黃線)出現了兩個峯,雖然RSS低,但目測擬合效果不好。bootstrap方法早就排除了Weibull,現在我們知道具體的原因了。
3、結合PDF特性做決策
還有五個候選分佈在擬合優度、bootstrap、可視化檢查上都表現不錯。現在要判斷哪個PDF的基本特性最適合建模人類身高,逐個分析:
對數伽馬分佈(Log-gamma)形狀偏斜,類似伽馬分佈但尾部更重。它對數值的對數建模,適合數據包含大量高值的情況。
Beta分佈通常用來建模比例或比率,不太適合身高這種連續變量。如果身高除以參考值(比如中位數),Beta才合適。所以雖然它擬合優度最好,目測也不錯但不是首選。
伽馬分佈(Gamma)是連續分佈,常用於正偏數據,即存在高值長尾。人類身高因為有特別高的個體,可能呈正偏分佈。但bootstrap顯示擬合不佳。
學生t分佈在小樣本或總體方差未知時可以替代正態分佈。它的尾部比正態分佈重,能更好地捕捉離羣值或偏態。小樣本情況下t分佈可以考慮,但樣本量增大後t分佈會接近正態分佈。
正態分佈是經典選擇,但人類身高的正態性假設未必適用所有人羣。它沒有重尾,可能捕捉不好離羣值。
另外還有兩個不顯著但可能的候選:
廣義極值分佈(GEV)可以建模人羣中的極值,比如最大值或最小值。它允許重尾,能捕捉離羣值或偏態。不過它通常用於極值分佈,而非連續變量的整體分佈。
Weibull分佈通常建模單調遞增或遞減趨勢的數據,比如失效時間。人類身高沒有明顯的單調趨勢,PDF/CDF/QQ圖也顯示不匹配。
綜合擬合優度、bootstrap、可視化、PDF特性,loggamma分佈在這個場景下是最佳選擇。需要的話可以指定loggamma重新擬合:
# Initialize for common or popular distributions.
dfit = distfit(distr='loggamma', alpha=0.01, bound='both')
# Estimate the best fit
results = dfit.fit_transform(X)
# Print model parameters
print(dfit.model)
# {'name': 'loggamma',
# 'score': 6.676334203908028e-05,
# 'loc': -1895.1115726427015,
# 'scale': 301.2529482991781,
# 'arg': (927.596119872062,),
# 'params': (927.596119872062, -1895.1115726427015, 301.2529482991781),
# 'color': '[#e41a1c](#e41a1c)',
# 'CII_min_alpha': 139.80923469906566,
# 'CII_max_alpha': 185.8446340627711}
# Save model
dfit.save('./human_height_model.pkl')4、對新樣本做預測
用擬合好的模型評估新樣本的顯著性,判斷它們是否偏離正常範圍(inlier)。預測基於理論概率密度函數,速度快、開銷小、結果可解釋。PDF的置信區間用
alpha參數設置。這裏需要領域知識,因為數據集裏沒有已知離羣值。這個例子設置置信區間(CII)
alpha=0.01,得到最小邊界139.8cm,最大邊界185.8cm。默認分析兩個尾部,可以用
bound參數調整。
predict函數可以對新樣本預測並畫圖(圖5)。注意顯著性做了多重檢驗校正:
multtest='fdr_bh'。所以離羣值可能在置信區間外但沒被標記為顯著。
# New human heights
y = [130, 160, 200]
# Make predictions
results = dfit.predict(y, alpha=0.01, multtest='fdr_bh', todf=True)
# The prediction results
results['df']
# y y_proba y_pred P
# 0 130.0 0.000642 down 0.000428
# 1 160.0 0.391737 none 0.391737
# 2 200.0 0.000321 up 0.000107
plt.figure();
fig, ax = plt.subplots(1, 2, figsize=(20, 8))
# PDF for only the best fit
dfit.plot(chart='PDF', ax=ax[0]);
# CDF for the top 10 fits
dfit.plot(chart='CDF', ax=ax[1])
# Show plot
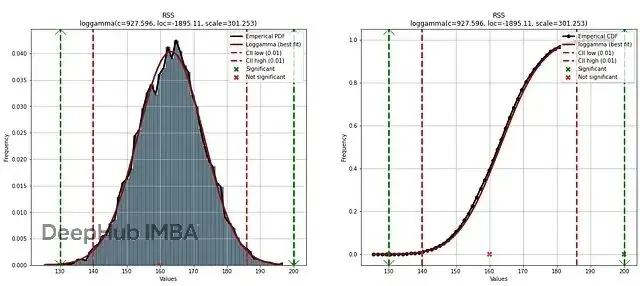
plt.show()圖5. 左圖:經驗數據直方圖和對數伽馬PDF。黑線是經驗分佈,紅線是擬合的理論分佈,紅色豎線是0.01的置信區間。綠色虛線標記為離羣值,紅叉不顯著
預測結果存在
results裏,包含幾列:
y、
y_proba、
y_pred、
P。
P是原始p值,
y_proba是多重檢驗校正後的概率(默認
fdr_bh)。用
todf=True參數會返回數據框。兩個觀測值概率
alpha<0.01,被標記為顯著的
up或
down。
真實數據的Anomaly檢測
前面演示瞭如何擬合模型並檢測novelty場景下的全局離羣值。現在用真實數據做anomaly檢測。真實數據通常更棘手。這裏用湯森路透的天然氣現貨價格數據集,下載導入並去除nan值後,有6555個數據點,跨度27年。
# Initialize distfit
dfit = distfit()
# Import dataset
df = dfit.import_example(data='gas_spot_price')
print(df)
# price
# date
# 2023-02-07 2.35
# 2023-02-06 2.17
# 2023-02-03 2.40
# 2023-02-02 2.67
# 2023-02-01 2.65
# ...
# 1997-01-13 4.00
# 1997-01-10 3.92
# 1997-01-09 3.61
# 1997-01-08 3.80
# 1997-01-07 3.82
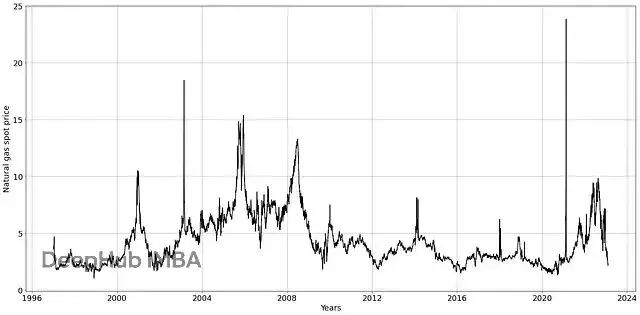
# [6555 rows x 1 columns]先畫個天然氣現貨價格的折線圖,看看有沒有明顯趨勢或其他特徵(圖6)。2003年和2021年有兩個明顯峯值,暗示全局異常。價格走勢有自然起伏,局部高低點。從折線圖能建立對分佈的初步判斷。價格主要在[2, 5]區間波動,但2003-2009年有幾個特殊年份,區間偏向[6, 9]。
# Get unique years
dfit.lineplot(df, xlabel='Years', ylabel='Natural gas spot price', grid=True)
# Show the plot
plt.show()圖6. 湯森路透天然氣現貨價格開源數據集
用distfit深入分析數據分佈,確定配套的PDF。搜索空間設為所有可用PDF,bootstrap設為100評估過擬合。
# Initialize
from distfit import distfit
# Fit distribution
dfit = distfit(distr='full', n_boots=100)
# Search for best theoretical fit.
results = dfit.fit_transform(df['price'].values)
# Plot PDF/CDF
fig, ax = plt.subplots(1,2, figsize=(25, 10))
dfit.plot(chart='PDF', n_top=10, ax=ax[0])
dfit.plot(chart='CDF', n_top=10, ax=ax[1])
# Show plot
plt.show()圖7. 左:PDF;右:CDF。所有擬合的理論分佈用不同顏色顯示
最佳擬合PDF是Johnsonb(圖7),但繪製經驗分佈時,PDF(紅線)沒有完全貼合經驗數據。多數數據點確實在[2, 5]區間(分佈峯值位置),分佈中還有個較小的第二峯,價格在6附近。這就是PDF擬合不夠平滑的地方,出現了欠擬合和過擬合。用摘要圖和QQ圖能更好地檢查擬合效果:
# Plot Summary and QQ-plot
fig, ax = plt.subplots(1,2, figsize=(25, 10))
# Summary plot
dfit.plot_summary(ax=ax[0])
# QQplot
dfit.qqplot(df['price'].values, n_top=10, ax=ax[1])
# Show the plot
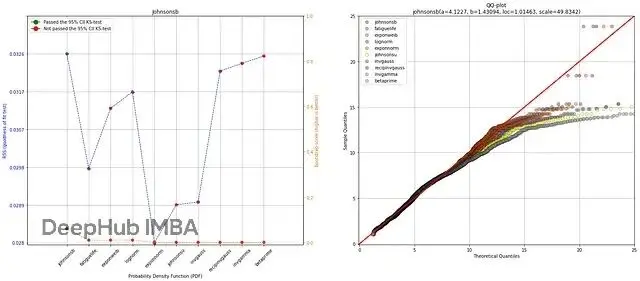
plt.show()摘要圖顯示擬合優度檢驗在所有top分佈上得分不錯(低分)。但看bootstrap結果,除了一個分佈,其他全都過擬合了(圖8A橙線)。這不意外,因為前面就注意到了過擬合和欠擬合。QQ圖證實擬合分佈與經驗數據偏差較大(圖8B)。只有Johnsonsb分佈勉強合格。
圖8. A. 左圖:PDF按bootstrap得分和擬合優度排序;B. 右圖:QQ圖,經驗分佈vs所有理論分佈
繼續用Johnsonsb分佈和
predict功能檢測離羣值。數據集包含離羣值,遵循anomaly方法——在正常樣本上擬合分佈,落在置信區間外的觀測標記為潛在離羣點。用
predict和
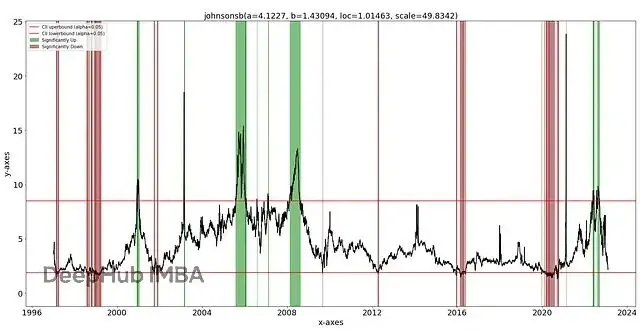
lineplot可以檢測並繪製離羣值。從圖9看,檢測到了全局離羣值,還有一些上下文離羣值,雖然沒有專門建模。紅條是低於下限的離羣值,綠條是高於上限的離羣值。
alpha參數可以調置信區間。
# Make prediction
dfit.predict(df['price'].values, alpha=0.05, multtest=None)
# Line plot with data points outside the confidence interval.
dfit.lineplot(df['price'], labels=df.index)圖9. 擬合分佈並預測後的離羣值可視化。綠條是95% CII上限外的離羣值,紅條是下限外的離羣值
總結
本文講了anomaly和novelty檢測的區別,演示瞭如何用分佈擬合創建離羣值檢測模型。distfit庫可以評估89個理論分佈,選出最佳模型,對新樣本做預測。通過實踐案例和真實數據,確定了最匹配的PDF。
有時候沒有理論分佈顯著匹配,distfit庫也提供了非參數擬合選項,用百分位數或分位數實現。更多細節可以看分佈擬合的相關博客。離羣值檢測本身就是個有挑戰的任務,"正常"或"預期"的定義因場景而異,有主觀性。離羣值可能源於測量誤差、數據錯誤或自然波動,下結論前要仔細分析偏差的根本原因。
https://avoid.overfit.cn/post/d56cd3ea448340059511f1489dfb1f05
作者:Erdogan T