🎈 作者:Eriktse
🎈 簡介:19歲,211計算機在讀,現役ACM銀牌選手🏆力爭以通俗易懂的方式講解算法!❤️歡迎關注我,一起交流C++/Python算法。(優質好文持續更新中……)🚀
🎈 閲讀原文獲得更好閲讀體驗:https://www.eriktse.com/algorithm/1147.html
A. Bits Reverse
題目鏈接:https://codeforces.com/gym/102823/problem/D
題意
給定兩個數字x和y,現在有一種操作:將y的二進制數的連續三位進行翻轉。問最少操作多少次可以使得x = y,或輸出-1表示無法使得x = y。
分析
因為每次固定選連續三位進行翻轉,我們可以想一下連續三位翻轉的一些性質。
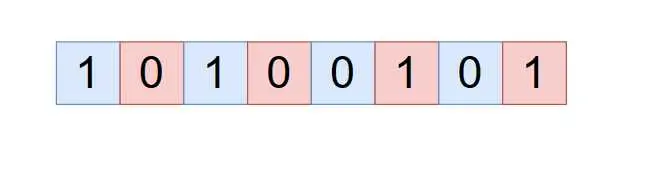
首先中間這個數字肯定是不變的,然後兩邊的數字swap一下。
也就是每次會選擇距離為2的兩個數字進行一次交換,那麼如果某個1在奇數位上,交換後依然在奇數位上,如果在偶數位上,交換後依然在偶數位上。
如下圖,紅色區域的二進制數和藍色區域的二進制數是相互獨立的。
所以我們可以進行奇偶分類的討論,求出在奇數位上所需的操作次數,然後再求在偶數位上所需的操作次數即可。
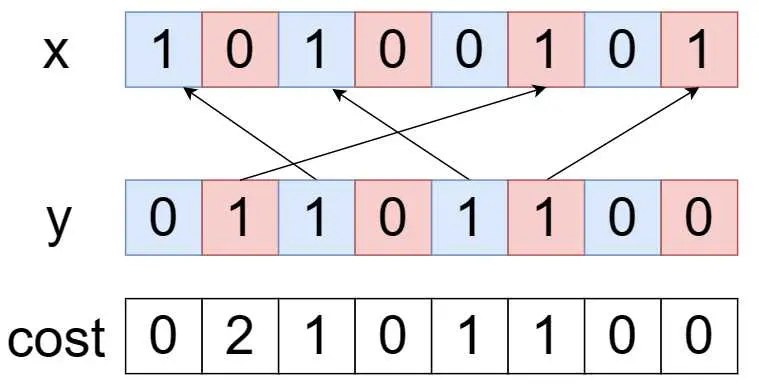
我們可以發現,如果要使得操作後x = y,那麼對於奇數位(即上圖中的藍色區域),y最高位的1一定對應x最高位的1,以此類推。而在奇數位上移動一格需要的操作次數是1次。
具體看下圖的對應關係:
代碼
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 105;
int a[N], b[N], pa, pb;
int kase;
int getabs(int x){return x < 0 ? -x : x;}
void solve()
{
cout << "Case " << ++ kase << ": ";
int x, y;cin >> x >> y;
pa = pb = 0;
int ans = 0;
for(int i = 0;i < 64; i += 2)
{
if(x >> i & 1)a[++ pa] = i;
if(y >> i & 1)b[++ pb] = i;
}
if(pa != pb)
{
cout << -1 << '\n';
return;
}
for(int i = 1;i <= pa; ++ i)ans += getabs(a[i] - b[i]) / 2;
pa = pb = 0;
for(int i = 1;i < 64; i += 2)
{
if(x >> i & 1)a[++ pa] = i;
if(y >> i & 1)b[++ pb] = i;
}
if(pa != pb)
{
cout << -1 << '\n';
return;
}
for(int i = 1;i <= pa; ++ i)ans += getabs(a[i] - b[i]) / 2;
cout << ans << '\n';
}
signed main()
{
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int _;cin >> _;
while(_ --)solve();
return 0;
}B. Empty Squares
題目鏈接:https://codeforces.com/gym/104252/problem/E
題意
給定一個長度為n,高度為1的矩形,現在你手上有高度均為1,長度分別為1, 2, 3, ..., n的共n個矩形,但你一開始已經放了一個長度為k的矩形到中間,並使得左邊空了e個格子。
問接下來你該怎麼不重疊地放置矩形,可以使得剩餘的空格最少,輸出最少空格個數。
分析
看一眼數據範圍,發現n只有1000,我們不放枚舉最終矩形的形態(即左邊有i個格子,中間k個格子,右邊e個格子),然後判斷一下這種情況能不能填滿。
現在問題就變為了寫一個函數f(l,k,r)求這種形態的矩形是否能夠被恰好不留空位地構造出來。
進行一個簡單的分類討論(不妨設l <= r):
| 限制條件 | 情況 |
|---|---|
| l != r != k | 一定可以,就是用長度分別為l,r,k的矩形填充即可。 |
| l = r = k | 當k >= 5時一定可以構造出來(1+4+5+2+3),其餘情況可以簡單手算一下發現一定不行。 |
| r=k | 兩個較大的相等,我們必須將r拆開,但是r可能拆出l,我們只需要枚舉1 + (r - 1)和2 + (r - 2)兩種情況即可,l至多等於這四個數字當中的一個,所以兩種情況必然有一種成立(注意保證i != r - i,拆出來的兩個數字也不能相等)。 |
| l=k或l=r | 類似的拆開l即可。 |
ok了。
代碼
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e3 + 9;
bool f(int l, int k, int r)
{
if(l != r && l != k && r != k)return true;
if(l > r)swap(l, r);
//l <= r
if(l == k && k == r)
{
return l > 4;
}else if(l == r || l == k)
{
for(int i = 1;i <= 2 && i < l - i; ++ i)
{
if(i != k && l - i != k)return true;
}
}else if(k == r)
{
for(int i = 1;i <= 2 && i < r - i; ++ i)
{
if(i != l && r - i != l)return true;
}
}
return false;
}
signed main()
{
int n, k, e;cin >> n >> k >> e;
int ans = n - k;
for(int i = 0;i <= e; ++ i)
{
for(int j = 0;j <= n - k - e; ++ j)
{
if(f(i, k, j))
{
//cout << "l, k, r = " << i << ' ' << k << ' ' << j << '\n';
ans = min(ans, n - i - j - k);
}
}
}
cout << ans << '\n';
return 0;
}C. Wall Painting
題意
給定n個數字(題目好像沒説清楚,應該是1e9以內的非負整數),求其中選出i個數字的所有組合的異或和之和。
分析
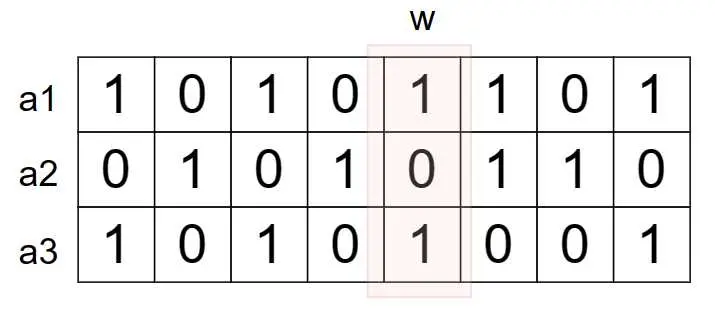
拆位,假設當前考慮的是第w位,那麼我們只需要枚舉出w位的所有組合情況並求和即可,不同位之互不影響(因為我們只需要所有的組合異或和之和)。
最外層枚舉從n個數字中選出的數字的個數,即i,然後對於第w位,得到這一位上的cnt0和cnt1分別表示二進制位上的0/1的個數(可以預處理出來)。
然後開始枚舉選j個1,自然就選i-j個0,且這種情況的貢獻為:
$$C_{cnt1}^{j} \times C_{cnt0}^{i-j} \times 2^w \times [j \% 2 = 1]$$
還有一種dp的寫法,我自己寫的時候是用dp的,比較sb,這就不寫了。
代碼
//C - Wall Painting
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1009, p = 1e6 + 3;
int C[N][N];
void init(int n)
{
for(int i = 0;i <= n; ++ i)C[i][0] = 1;
for(int i = 1;i <= n; ++ i)
for(int j = 1;j <= n; ++ j)
C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % p;
}
int n;
int a[N], c[50][2];
void solve()
{
for(int i = 1;i <= n; ++ i)cin >> a[i];
memset(c, 0, sizeof c);
for(int i = 1;i <= n; ++ i)
for(int j = 0;j <= 40; ++ j)
c[j][a[i] >> j & 1] ++;
//枚舉選擇的數字的個數i
for(int i = 1;i <= n; ++ i)
{
int ans = 0;
//枚舉位數
for(int w = 0;w <= 40; ++ w)
{
//在這一位上選擇j個1和(i - j)個0
for(int j = 1;j <= i && j <= c[w][1]; j += 2)
{
ans = (ans + (1ll << w) * C[c[w][1]][j] % p * C[c[w][0]][i - j] % p) % p;
}
}
cout << ans << " \n"[i == n];
}
}
signed main()
{
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
init(1002);
while(cin >> n)solve();
return 0;
}