導讀

本文探討了圖譜Embedding在業務安全與反作弊等關鍵業務場景中的應用，特別是在異常檢測方面。傳統的統計方法在面對複雜多變的攻擊場景時顯得力不從心，因此本文介紹了一種基於One-Hot編碼的圖譜Embedding算法GEE，通過標籤傳播實現結點特徵的表達。作者還通過兩篇論文的代碼驗證，發現稀疏矩陣改進版算法在測試數據集上性能不佳，並進一步優化了算法，使其在計算效率上有所提升。本文對於利用圖譜數據進行異常檢測的研究和實踐具有一定的指導意義。

在安全監控與反作弊等關鍵業務場景中，對流量數據和用户行為進行異常檢測是不可或缺的基石。傳統的方法涉及在各個業務層面上對流量和用户行為進行統計分析，提取關鍵指標特徵，並在時間軸上對這些特徵進行建模分析。藉助相關算法，我們可以檢測當前指標值是否偏離了其在歷史數據中的正常分佈模式。

然而，隨着攻擊手段的不斷演變，單純的統計方法在面對複雜多變的攻擊場景時已顯得力不從心。尤其對於規模較小、缺乏顯著聚集特徵的攻擊行為，傳統的統計方法往往難以奏效。在此情境下，我們常需藉助多種輔助手段來聚合樣本，並對聚合後的樣本進行統計建模分析，以判斷其是否異常。

在之前的文章:Embedding空間中的時序異常檢測，我已詳細介紹了一種利用特徵Embedding聚類來建模用户行為並進行異常檢測的方法。另一種常用的樣本聚合手段則是藉助圖譜數據來識別團伙行為。由此，一個自然而然的思路是，若能恰當地對圖譜數據進行Embedding處理，我們便能複用前述方法，對團伙行為進行異常檢測。

然而，圖譜數據的Embedding處理歷來成本高昂，無論是計算成本還是存儲成本都頗為可觀。在業務實踐中，我們所涉及的數據規模通常極為龐大，且異常檢測對計算時效性有着一定的要求。因此，圖譜Embedding的應用範圍長期受到限制。
不過，近期我偶然發現的兩篇論文或許能為我們帶來轉機。以下是論文的原文鏈接：

• https://arxiv.org/abs/2109.13098
• https://arxiv.org/abs/2406.03726

01 GEE算法簡介

在第一篇論文中，作者提出了一種基於One-Hot編碼的圖譜Embedding算法——GEE(Graph Encoder Embedding)。

GEE算法的偽碼如上，可以看到該算法的原理並不複雜，核心步驟如下：

1. 首先構造輸入數據：

a. E: 圖譜的邊集，是一個三元組的列表，每個元組的三個元素分別代表兩個頂點的索引值，以及邊的權重。

b. Y: 圖譜的頂點集，是一個整數列表，長度為N, 每個元素為相應頂點的標籤，取值範圍為[0, K], K為標籤的類別數量。

2. 初始化Embedding矩陣與權重矩陣：

a. Z: 頂點Embedding矩陣，維度為[N,K]，其中N是頂點的數量，K是Embedding的維度，同時也是項點標籤的類別數量。

b. W: 權重矩陣，維度同樣為[N,K]，含義同上。

3. 計算權重矩陣：

a. 針對每一種標籤K，計算其對應的權重：

i. 查找該標籤對應的頂點數量，記為n_k。

ii. 將該標籤對應的項點與該標籤的關係權重點設置為\frac{1}{n_k}

4. 計算Embedding矩陣：

a. 針對E中的每一條邊： i: 將Z中源頂點與目標頂點標籤對應的Embedding值，與權重矩陣中的目標頂點與目標項點標籤對應的權重值與邊的權重的乘積相加

ii：將Z中目標頂點與源頂點標籤對應的Embedding值，與權重矩陣中的源頂點與源項點標籤對應的權重值與邊的權重的乘積相加

從上面的過程不難看出，算法的核心思想其實是標籤傳播，通過在傳播過程進行適當的加權，實現結點特徵的表達。更多細節可以參考論文原文。從論文中的實驗提供的數據來看，該算法在效果上略遜於隨機遊走算法，但在計算效率上有着數量級的提升。

在第二篇論文中，作者利用稀疏矩陣計算庫scipy.sparse，對GEE算法進行了改進，進一步提高了計算效率。同時還提供了可以直接使用的實現代碼。

02 算法驗證

由於算法的原理實在太過簡單，不免讓人懷疑其在真實業務場景中是否真的有效，因此，需要利用真實數據來驗證算法的有效性。

2.1 數據準備

從業務日誌中抽取了用户ID、IP、設備ID、瀏覽器ID等字段做為頂點，建立了用户行為圖譜，圖譜中包含了約1000萬條邊。

針對IP、設備ID、瀏覽器ID等頂點，分別符加了地域（省份）、操作系統等標籤，標籤的維度為50。標籤規則如下：

• 所有的用户ID頂點，標籤統一為0
• IP頂點，標籤為IP所屬的省份的編號（1~34，未知為0） + 1
• 設備ID頂點，設備的操作系統編號（1~6，未知為0） + 36
• 瀏覽器ID頂點，瀏覽器的操作系統編號（1~6，未知為0） + 43

舉例説明：

• 某個IP頂點，其所屬省份的編號為10，其標籤為11
• 某個設備頂點，其操作系統編號為3，其標籤為39

2.2 算法初步驗證

兩篇論文均附帶了參考實現的代碼，然而，第一篇論文提供的代碼需要經過修改才能順利運行，相比之下，第二篇論文提供的代碼則可直接執行。因此，在驗證原始算法時，採用了第二篇論文中提供的Python實現代碼（訪問鏈接：https://github.com/xihan-qin/GEE_sparse）。

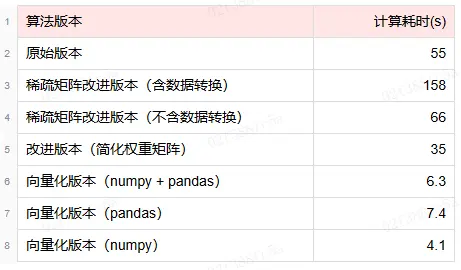
在性能方面，我們對數據集進行了Embedding計算。結果顯示，原始算法耗時約55秒，這一表現符合預期並具有實用價值。然而，令人驚訝的是，稀疏矩陣改進版的算法耗時高達約158秒，性能並未有所提升，反而有所下降。深入分析後發現，改進後的算法在計算過程中，需先將原始邊集轉換為稀疏矩陣，再借助scipy.sparse庫進行計算，該轉換過程便耗時約90秒。即便不計入這一轉換時間，改進後的算法在我們的測試數據集上的表現仍不及原始算法。

在審閲參考實現代碼的過程中，我們還發現了以下問題：

• 由於每個頂點僅有一個標籤，因此同類頂點在權重矩陣W中的值相同。這意味着原始算法的權重矩陣W在計算和存儲結構上均可進行簡化。
• 原始算法的Embedding矩陣計算過程中，每次僅處理一條邊，未能充分利用現代CPU的向量化計算能力。
• 稀疏矩陣改進版的算法在計算Embedding矩陣時，採用矩陣乘法一次性處理所有邊，雖能利用CPU的向量化計算能力，但在數據量較大時，會嚴重依賴內存容量與帶寬，導致計算效率降低。這可能是該算法在測試數據集上性能不佳的原因。

看到這裏，做為一個資深碼農，已經按耐不住要對算法再次進行改進了。

03 算法改進

3.1 簡化權重矩陣

首先是簡化了權重矩陣的版本，同時也作為後續改進的基準版本。

def graph_encode_embedding(X, Y, n_K, show_prog=False):
    """
    compute the edge embedding matrix Z and node weight matrix W
    參考論文的原始實現

    :param X: edge list, list of tuple, [(src, dst, weight), ...]
    :param Y: node label, array of int, [node_label, ...]
    :param n_K: number of classes
    :return: Z, W
    """
    # 初始化權重矩陣W
    W = np.zeros(n_K)
    # 遍歷每個類別
    for k in range(n_K):
        # 統計每個類別的節點數量
        W[k] = (Y == k).sum()
    # 計算每個類別的權重，即每個類別節點數量的倒數，為了避免除零錯誤，分母加1
    W = 1 / (W + 1)
    # 初始化節點嵌入矩陣Z，該矩陣的行數是節點的數量，列數是類別的數量，實際上是保存了每個節點與每個類別之間的相關性權重
    Z = np.zeros((Y.shape[0], n_K))

    # 初始化Jupyter進度條
    if show_prog:
        total = len(X)
        steps = 0
        prog_bar = ProgressBar(100)
        prog_bar.display()

    # 遍歷每一條邊，更新對應節點的嵌入向量
    for src, dst, edg_w in X:
        # 取出邊的源節點和目標節點的標籤
        src = int(src)
        dst = int(dst)
        label_src = Y[src]
        label_dst = Y[dst]
        # 如果目標節點有標籤（>=0），則更新源節點的嵌入向量
        if label_dst >= 0:
            # 更新源節點的嵌入向量，對源節點與目標節點對應的類別的權重進行累加
            Z[src, label_dst] = Z[src, label_dst] + W[label_dst] * edg_w
        # 如果源節點有標籤（>=0）且不是自環，則更新目標節點的嵌入向量
        if (label_src >= 0) and (src != dst):
            # 更新目標節點的嵌入向量，對目標節點與源節點對應的類別的權重進行累加
            Z[dst, label_src] = Z[dst, label_src] + W[label_src] * edg_w

        # 更新進度條
        if show_prog:
            steps += 1
            prog = int(steps / total * 100)
            if prog > prog_bar.progress:
                prog_bar.progress = prog

    # 返回節點嵌入矩陣Z和節點權重矩陣W
    return Z, W

由於每個頂點僅有一個標籤，因此同類頂點在權重矩陣W中的值相同，也就是説其實只需要針對每個標籤存儲其對應的權重即可。這裏將權重矩陣W簡化為一個K維向量，其每個元素代表了對應標籤的權重。

此外，在計算權重時，由於我們實際的數據中會存在某個分類標籤下沒有頂點的情況，因此，在計算權重時進行了容錯處理。這會導致最終Embedding的計算結果與原始算法存在細微差異，但理論上應該不影響最終的Embedding效果。

為驗證改進後的算法的結果與原始算法一致，重新構造隨機生成的測試數據，在不添加容錯處理的情況下，驗證改進後的算法與原始算法的結果是否完全一致。之後再添加容錯處理，並做為後續改進的基準版本。

該版本算法在業務數據測試集上的計算耗時約為35秒，已經比較原始算法有了明顯的性能提升。

3.2 支持mini-batch的向量化計算版本

接下來是對Embedding計算過程的改進，主要思路是利用向量化計算，減少不必要的循環。同時利用mini-batch的方式，減少內存的佔用。

def graph_encode_embedding_batched(X, Y, n_K, batch_size=1024, show_prog=False):
    """
    compute the edge embedding matrix Z and node weight matrix W
    向量化版本，支持mini-batch，依賴numpy和pandas

    :param X: edge list, array of float, [[src, dst, weight], ...]
    :param Y: node label, array of int, [node_label, ...]
    :param n_K: number of classes
    :return: Z, W
    """
    # 初始化權重矩陣W
    W = np.zeros(n_K)
    # 遍歷每個類別
    for k in range(n_K):
        # 統計每個類別的節點數量
        W[k] = (Y == k).sum()
    # 計算每個類別的權重，即每個類別節點數量的倒數，為了避免除零錯誤，分母加1
    W = 1 / (W + 1)
    # 初始化節點嵌入矩陣Z，該矩陣的行數是節點的數量，列數是類別的數量，實際上是保存了每個節點與每個類別之間的相關性權重
    Z = np.zeros((Y.shape[0], n_K))
    # 記錄總的邊數
    total = len(X)

    # 初始化Jupyter進度條
    if show_prog:
        prog_bar = ProgressBar(100)
        prog_bar.display()

    # 向量化方式處理所有的邊，每次處理batch_size條邊
    for batch_id in range(0, total, batch_size):
        # 獲取當前batch的邊信息
        batch = slice(batch_id, batch_id + batch_size)
        src = X[batch, 0].astype(int)
        dst = X[batch, 1].astype(int)
        edge_w = X[batch, 2]
        # 提取源節點和目標節點的標籤，注意，這裏的src和dst中保存的都是節點的索引，不是節點的標籤
        # 得到的src_label和dst_label是節點的標籤，與src和dst一樣都是以邊索引為索引的數組
        src_label = Y[src]
        dst_label = Y[dst]

        # 首先處理目標節點，篩選有標籤的目標節點，注意，dst_valid是邊的索引，不是節點的索引
        dst_valid = np.where(dst_label >= 0)[0]
        # 篩選出有效目標節點的標籤
        dst_label = dst_label[dst_valid]
        # 篩選出有效目標節點的邊權重
        dst_edge_w = edge_w[dst_valid]
        # 篩選出有效目標節點的源節點
        dst_valid_src = src[dst_valid]
        # 將有效目標節點的信息轉換為DataFrame，並按照源節點和標籤進行分組，計算每個源節點與每個標籤的權重和
        df = pd.DataFrame({"src": dst_valid_src, "label": dst_label, "weight": dst_edge_w * W[dst_label]})
        df = df.groupby(["src", "label"], as_index=False).sum()
        # 將有效目標節點的信息更新到節點嵌入矩陣Z中
        Z[df["src"], df["label"]] += df["weight"]

        # 然後處理源節點，篩選有標籤且不是自環的源節點，過程與目標節點類似
        src_valid = np.where((src_label >= 0) & (src != dst))[0]
        src_label = src_label[src_valid]
        src_edge_w = edge_w[src_valid]
        src_valid_dst = dst[src_valid]
        # 將有效源節點的信息轉換為DataFrame，並按照目標節點和標籤進行分組，計算每個目標節點與每個標籤的權重和，更新到節點嵌入矩陣Z中
        df = pd.DataFrame({"dst": src_valid_dst, "label": src_label, "weight": src_edge_w * W[src_label]})
        df = df.groupby(["dst", "label"], as_index=False).sum()
        Z[df["dst"], df["label"]] += df["weight"]

        # 更新進度條
        if show_prog:
            prog = min(int((batch_id + batch_size) / total * 100), 100)
            if prog > prog_bar.progress:
                prog_bar.progress = prog

    # 返回節點嵌入矩陣Z和節點權重矩陣W
    return Z, W

該版本算法在業務數據測試集上的計算耗時約為6.3秒，相比原始算法有了接近數量級的性能提升。

不過這版的算法實現中，同時使用了numpy和pandas兩個庫，做為一個“強迫症患者”，還是儘量只依賴一個庫來實現比較好。

3.3 Pandas版本

由於算法中需要進行分組求知，而numpy中沒有提供可以直接使用的groupby功能，因此先嚐使用pandas來實現。

def graph_encode_embedding_batched_pd(X, Y, n_K, batch_size=10240, show_prog=False):
    """
    compute the edge embedding matrix Z and node weight matrix W
    向量化版本2，支持mini-batch，只依賴pandas，用於性能測試

    :param X: edge list, array of float, [[src, dst, weight], ...]
    :param Y: node label, array of int, [node_label, ...]
    :param n_K: number of classes
    :return: Z, W
    """
    # 初始化權重矩陣W
    W = np.zeros(n_K)
    # 遍歷每個類別
    for k in range(n_K):
        # 統計每個類別的節點數量
        W[k] = (Y == k).sum()
    # 計算每個類別的權重，即每個類別節點數量的倒數，為了避免除零錯誤，分母加1
    W = 1 / (W + 1)
    # 初始化節點嵌入矩陣Z，該矩陣的行數是節點的數量，列數是類別的數量，實際上是保存了每個節點與每個類別之間的相關性權重
    Z = np.zeros((Y.shape[0], n_K))
    # 記錄總的邊數
    total = len(X)

    # 初始化Jupyter進度條
    if show_prog:
        prog_bar = ProgressBar(100)
        prog_bar.display()

    # 向量化方式處理所有的邊，每次處理batch_size條邊
    for batch_id in range(0, total, batch_size):
        # 獲取當前batch的邊信息
        batch = slice(batch_id, batch_id + batch_size)
        # 將邊信息轉換為DataFrame
        df = pd.DataFrame(X[batch], columns=["src", "dst", "edge_w"])
        df.astype({"src": int, "dst": int}, copy=False)
        # 添加源節點和目標節點的標籤
        df["src_label"] = Y[df["src"]]
        df["dst_label"] = Y[df["dst"]]

        # 篩選有標籤的目標節點
        df_dst_valid = df[df.dst_label >= 0]
        # 計算每個目標節點的權重
        df_dst_valid["weight"] = df_dst_valid["edge_w"] * W[df_dst_valid["dst_label"]]
        # 按照源節點和標籤進行分組，計算每個源節點與每個標籤的權重和
        df_dst_valid = df_dst_valid.groupby(["src", "dst_label"], as_index=False).sum()
        # 將有效目標節點的信息更新到節點嵌入矩陣Z中
        Z[df_dst_valid["src"], df_dst_valid["dst_label"]] += df_dst_valid["weight"]

        # 篩選有標籤且不是自環的源節點
        df_src_valid = df[df.src_label >= 0]
        # 計算每個源節點的權重
        df_src_valid["weight"] = df_src_valid["edge_w"] * W[df_src_valid["src_label"]]
        # 按照目標節點和標籤進行分組，計算每個目標節點與每個標籤的權重和
        df_src_valid = df_src_valid.groupby(["dst", "src_label"], as_index=False).sum()
        # 將有效源節點的信息更新到節點嵌入矩陣Z中
        Z[df_src_valid["dst"], df_src_valid["src_label"]] += df_src_valid["weight"]

        # 更新進度條
        if show_prog:
            prog = min(int((batch_id + batch_size) / total * 100), 100)
            if prog > prog_bar.progress:
                prog_bar.progress = prog

    # 返回節點嵌入矩陣Z和節點權重矩陣W
    return Z, W

該版本算法在業務數據測試集上的計算耗時約為7.4秒，仍然很快，但......

3.4 Numpy版本

由於numpy中沒有提供可以直接使用的groupby功能，需要基於numpy現在函數來自己實現相似的功能，在查找了相關資料，反覆蓋閲讀了numpy的手冊，並多次嘗試後，終於找到了在numpy中使用groupby的方法。

def group_sum(indexes, values):
    """
    sum values by index
    根據索引求和, 相當於: values.groupby(indexes).sum()

    :param indexes: array of int, [[index1, index2, ...], ...]
    :param values: array of float, [value1, value2, ...]
    :return: grp_indexes, grp_sums
    """
    if indexes.ndim == 1:
        # 若索引只有一列，可以直接使用
        reindex = indexes
    else:
        # 若索引有多個列，需要進行合併，生成一個新的唯一索引，這裏假定索引中都是整數。
        reindex = np.zeros(indexes.shape[0], dtype=indexes.dtype)
        for axis in reversed(range(indexes.shape[-1])):
            reindex = indexes[:, axis] * (reindex.max() + 1) + reindex
    # 對索引和數據進行排序
    order = np.argsort(reindex)
    sorted_reindex = reindex[order]
    sorted_indexes = indexes[order]
    sorted_values = values[order]
    # 對索引進行分組，生成組別索引，索引中的每個元素表示該組的第一個元素在原數組中的位置
    _, grp_idx = np.unique(sorted_reindex, return_index=True)
    # 對每個組的數據求和，這裏的reduceat是實現GroupBy的核心，它會根據grp_idx中的位置索引，對sorted_values進行分段的reduce操作。
    grp_sums = np.add.reduceat(sorted_values, grp_idx, axis=0)
    # 對索引進行還原
    grp_indexes = sorted_indexes[grp_idx]
    # 返回組別索引和組和
    return grp_indexes, grp_sums

有了這個函數，就可以實現純numpy版本的改進算法了。

def graph_encode_embedding_batched_np(X, Y, n_K, batch_size=1024, show_prog=False):
    """
    compute the edge embedding matrix Z and node weight matrix W
    向量化版本，支持mini-batch，只依賴numpy

    :param X: edge list, array of float, [[src, dst, weight], ...]
    :param Y: node label, array of int, [node_label, ...]
    :param n_K: number of classes
    :return: Z, W
    """
    # 初始化權重矩陣W
    W = np.zeros(n_K)
    # 遍歷每個類別
    for k in range(n_K):
        # 統計每個類別的節點數量
        W[k] = (Y == k).sum()
    # 計算每個類別的權重，即每個類別節點數量的倒數，為了避免除零錯誤，分母加1
    W = 1 / (W + 1)
    # 初始化節點嵌入矩陣Z，該矩陣的行數是節點的數量，列數是類別的數量，實際上是保存了每個節點與每個類別之間的相關性權重
    Z = np.zeros((Y.shape[0], n_K))
    # 記錄總的邊數
    total = len(X)

    # 初始化Jupyter進度條
    if show_prog:
        prog_bar = ProgressBar(100)
        prog_bar.display()

    # 向量化方式處理所有的邊，每次處理batch_size條邊
    for batch_id in range(0, total, batch_size):
        # 獲取當前batch的邊信息
        batch = slice(batch_id, batch_id + batch_size)
        src = X[batch, 0].astype(int)
        dst = X[batch, 1].astype(int)
        edge_w = X[batch, 2]
        # 提取源節點和目標節點的標籤，注意，這裏的src和dst中保存的都是節點的索引，不是節點的標籤
        # 得到的src_label和dst_label是節點的標籤，與src和dst一樣都是以邊索引為索引的數組
        src_label = Y[src]
        dst_label = Y[dst]

        # 首先處理目標節點，篩選有標籤的目標節點，注意，dst_valid是邊的索引，不是節點的索引
        dst_valid = np.where(dst_label >= 0)[0]
        # 篩選出有效目標節點的標籤
        dst_label = dst_label[dst_valid]
        # 篩選出有效目標節點的邊權重
        dst_edge_w = edge_w[dst_valid]
        # 篩選出有效目標節點的源節點
        dst_valid_src = src[dst_valid]
        # 源節點和標籤進行分組，計算每個源節點與每個標籤的權重和
        dst_indexes = np.array([dst_valid_src, dst_label]).T
        dst_weights = dst_edge_w * W[dst_label]
        dst_grp_indexes, dst_grp_weights = group_sum(dst_indexes, dst_weights)
        # 將有效目標節點的信息更新到節點嵌入矩陣Z中
        Z[dst_grp_indexes[:, 0], dst_grp_indexes[:, 1]] += dst_grp_weights

        # 然後處理源節點，篩選有標籤且不是自環的源節點，過程與目標節點類似
        src_valid = np.where((src_label >= 0) & (src != dst))[0]
        src_label = src_label[src_valid]
        src_edge_w = edge_w[src_valid]
        src_valid_dst = dst[src_valid]
        # 按照目標節點和標籤進行分組，計算每個目標節點與每個標籤的權重和，更新到節點嵌入矩陣Z中
        src_indexes = np.array([src_valid_dst, src_label]).T
        src_weights = src_edge_w * W[src_label]
        src_grp_indexes, src_grp_weights = group_sum(src_indexes, src_weights)
        Z[src_grp_indexes[:, 0], src_grp_indexes[:, 1]] += src_grp_weights

        # 更新進度條
        if show_prog:
            prog = min(int((batch_id + batch_size) / total * 100), 100)
            if prog > prog_bar.progress:
                prog_bar.progress = prog

    # 返回節點嵌入矩陣Z和節點權重矩陣W
    return Z, W

該版本算法在業務數據測試集上的計算耗時約為4.1秒。

3.5 算法改進小結

3.6 效果驗證

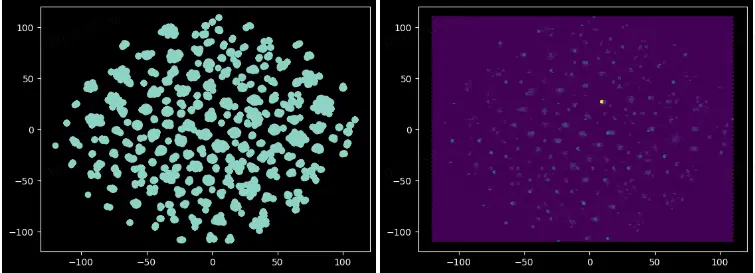
對Embedding的結果抽樣並通過TSNE進行可視化，結果如下：

                                 △散點圖                                                                           △HexBin圖

從圖中可以看到頂點呈現出明顯的聚類特徵，説明Embedding的結果是有意義的。但是在用於異常檢測時的效果的效果是否能真的能夠達到我們的預期，且聽下回分解。

————END————

推薦閲讀

AIAPI - 轉向AI原生檢索

學校新來了一位AI作文老師：能看、會評、還教改寫

搞定十萬卡集羣！貧窮限制了我的想象力…

AI Agent重塑微服務治理

百度智能雲千帆大模型平台引領企業創新增長