通過 RC 放電電路,看見自然選擇的數字:e
在 RC 放電電路中,我們總會看到這樣的公式:
$$ v(t) = V_0 e^{-t/RC} $$
很多人會好奇:為什麼偏偏是 e?它是怎麼"長"出來的?
這並不是數學家強行塞進去的結果,而是:
從 KCL 出發,用元件本身的物理規律,一步步推到微分方程,再用最基礎的積分和指數運算,$e$ 自然冒出來。
本文就用 $RC$ 放電電路 做主線,從電路基礎一步步算到 $e$,然後順帶看看:類似的指數行為,在自然界裏還有多少"親戚"。
一、RC 放電電路:從 KCL 開始
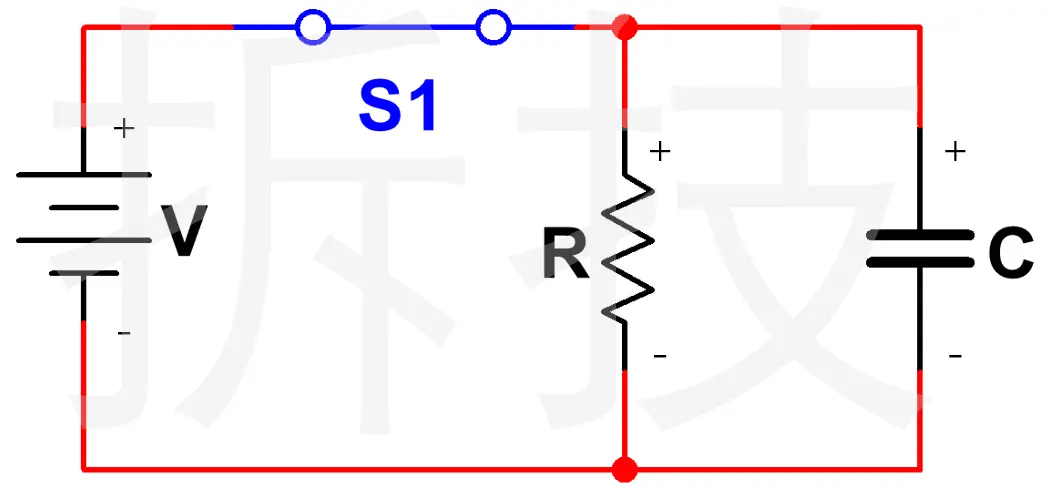
先看一個最基本的放電電路:
在$t_0$時刻前開關一直處於閉合狀態,,系統整個狀態穩定,此時,C電容兩端電壓$V$
在開關打開瞬間,電壓保持,此時$V_0=V$
- 電容 $C$,在 $t=0$ 時電壓為 $V_0$
- 電阻 $R$,與電容串聯
- 放電時刻起,電容通過電阻向地放電
- 節點電壓記為 $v(t)$
示意圖可以想象為:電容 $C$ 與電阻 $R$ 串聯,電容上端節點電壓為 $v(t)$,電阻下端接地。
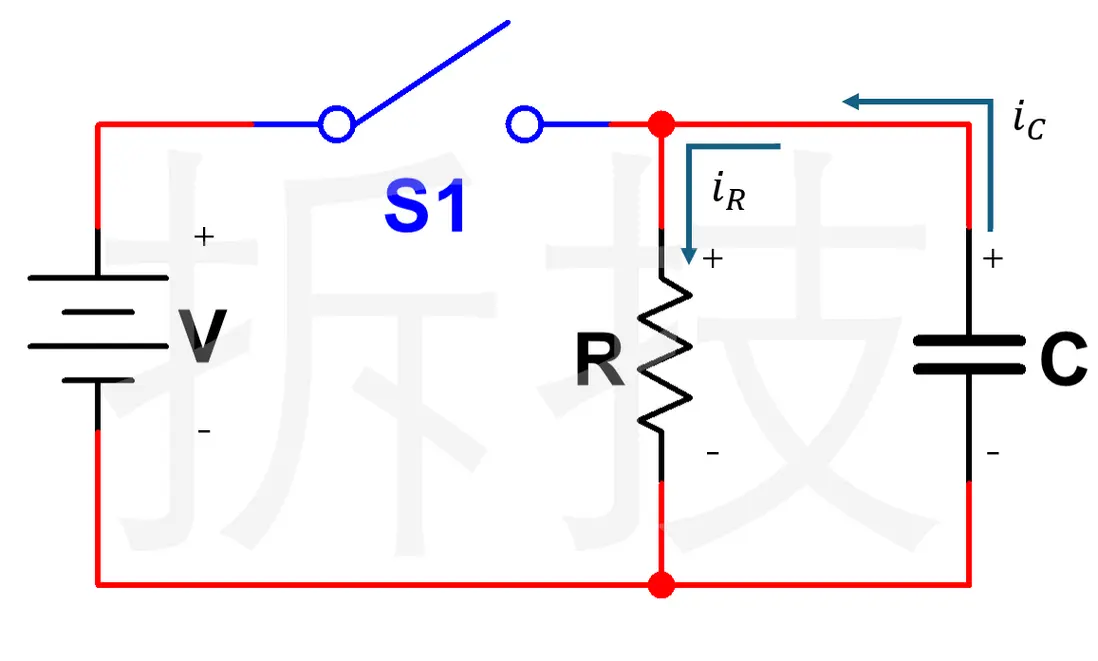
取電容與電阻連接處為節點,寫 KCL。約定:從節點流出的電流為正,則:
$$ i_R + i_C = 0 $$
1. 電阻支路電流
電阻兩端電壓為 $v(t)$,下端接地:
$$ i_R = \frac{v(t)}{R} $$
2. 電容支路電流
電容電流與電壓的關係是:
$$ i_C = C\frac{dv(t)}{dt} $$
這裏的 $C$ 是電容值,我們後面不會再讓任何"積分常數"也叫 $C$,避免混亂。
把兩個電流表達式代回 KCL:
$$ \frac{v(t)}{R} + C\frac{dv(t)}{dt} = 0 $$
整理,把導數項單獨放一邊:
$$ C\frac{dv(t)}{dt} = -\frac{v(t)}{R} $$
兩邊同除以 $C$:
$$ \frac{dv(t)}{dt} = -\frac{1}{RC}v(t) $$
到這裏為止,我們只用了:
- KCL
- 歐姆定律
- 電容電流公式
完全是“電路基礎”,還沒出現任何指數或對數。
二、變量分離:為積分做準備
從上面的微分方程:
$$ \frac{dv}{dt} = -\frac{1}{RC}v $$
把含 $v$ 的量挪到左邊,含 $t$ 的挪到右邊:
$$ \frac{1}{v}dv = -\frac{1}{RC}dt $$
這一步叫變量分離,目的是為了:
左邊只對 $v$ 積分,右邊只對 $t$ 積分。
三、關鍵一步:$\int \frac{1}{v}dv$ 為啥變成 $\ln v$?
接下來,我們對兩邊積分。這裏可以直接做 定積分,把初始條件寫進去。
在 $t = 0$ 時,電容電壓為:
$$ v(0) = V_0 $$
在任意時刻 $t$ 電壓為 $v(t)$,於是:
$$ \int_{V_0}^{v(t)} \frac{1}{v}dv = \int_0^{t} -\frac{1}{RC}dt $$
這時用到一個非常基礎的高中數學知識(可以在文章裏點名説清楚):
💡 數學結論(高中水平):
$$ \int \frac{1}{v}dv = \ln|v| + C $$
以及
$$ \frac{d}{dv}\ln v = \frac{1}{v} $$
也就是説:
- $\ln v$ 的導數是 $\frac{1}{v}$
- $\frac{1}{v}$ 的積分就是 $\ln v$(加上常數)
所以左邊的定積分:
$$ \int_{V_0}^{v(t)} \frac{1}{v}dv = \ln v(t) - \ln V_0 $$
右邊的定積分很簡單:
$$ \int_0^{t} -\frac{1}{RC}dt = -\frac{t}{RC} $$
於是有:
$$ \ln v(t) - \ln V_0 = -\frac{t}{RC} $$
把對數合併一下:
$$ \ln \frac{v(t)}{V_0} = -\frac{t}{RC} $$
到這裏為止,我們是:
- 從電路方程出發
- 通過變量分離
- 用高中知識:$\int \frac{1}{v}dv = \ln|v| + C$
自然得到一個對數方程。
四、取指數:$e$ 在這裏被"請出來"
有了:
$$ \ln \frac{v(t)}{V_0} = -\frac{t}{RC} $$
我們想把 "$\ln$" 去掉,就要用它的反函數——以 $e$ 為底的指數函數。也就是説,對兩邊做同樣的運算:取 $e$ 的指數:
$$ e^{\ln \frac{v(t)}{V_0}} = e^{-\frac{t}{RC}} $$
左邊根據 $e^{\ln x} = x$:
$$ \frac{v(t)}{V_0} = e^{-\frac{t}{RC}} $$
於是直接得到:
$$ \boxed{v(t) = V_0 e^{-\frac{t}{RC}}} $$
到這裏,$e$ 並不是"我們很喜歡它所以寫出來",而是:
由於 $\frac{1}{v}$ 的積分是 $\ln v$,而 $\ln$ 的反函數是 $e^{(\cdot)}$,所以最終的解必然是以 $e$ 為底的指數。
五、時間常數 $RC$ 的物理意義:36.8%
從公式:
$$ v(t) = V_0 e^{-t/RC} $$
取 $t = RC$:
$$ v(RC) = V_0 e^{-1} \approx 0.367 V_0 $$
也就是説:
經過一個時間常數 $RC$,電壓衰減到初值的約 36.8%。
這個比例 與 $R$ 和 $C$ 的具體數值無關,只和它們的乘積 $RC$ 有關。
這就是為什麼我們説:
- $RC$ 是"時間常數"
- 它決定了放電過程的"快慢節奏"
六、從 $RC$ 放電,看到自然界的"指數家族"
$RC$ 放電是最簡單的一階系統,而它的數學形式:
$$ \frac{dv}{dt} = -\frac{1}{RC}v $$
其實是一個非常通用的結構:
變化率 ∝ 當前狀態本身
任何符合這條規律的系統,都會產生類似的指數解:
$$ x(t) = x_0 e^{kt} $$
比如:
1. 放射性衰變
剩餘原子核數量 $N(t)$ 隨時間減少的速度,與當前數量成正比:
$$ \frac{dN}{dt} = -\lambda N \quad\Rightarrow\quad N(t) = N_0 e^{-\lambda t} $$
2. 藥物在人體內代謝
藥物濃度 $C(t)$ 的下降速度,往往和當前濃度成比例:
$$ C(t) = C_0 e^{-kt} $$
這就是所謂“半衰期”、“消除常數”的來源。
3. 熱物體冷卻(牛頓冷卻定律)
物體温度與環境温度差值 $\Delta T$ 的變化率,正比於當前温差:
$$ \frac{d}{dt}(T - T_{\text{env}}) = -k(T - T_{\text{env}}) $$
解為:
$$ T(t) - T_{\text{env}} = (T_0 - T_{\text{env}}) e^{-kt} $$
4. 理想情況下的種羣增長
在資源尚充足、空間不限制時,種羣增長率近似正比於當前種羣數量:
$$ \frac{dP}{dt} = kP \Rightarrow P(t) = P_0 e^{kt} $$
這些例子背後,都有一句統一的話:
"你現在有多少,就決定你變化得多快。"
於是,指數函數就成了它們共同的“語言”。
七、為什麼底數必須是 $e$,而不是 2、10 或別的數?
從數學角度,任何底數 $a > 0$ 且 $a \neq 1$ 都可以寫指數函數 $a^x$,但只有以 $e$ 為底時,性質最"乾淨":
$$ \frac{d}{dx} e^{x} = e^{x} $$
也就是説:
以 $e$ 為底的指數函數,它的變化率與自己"同形",只差一個係數。
這就是為什麼:
- 只要寫下 $\frac{dx}{dt} = kx$,
- 解出來必然是 $x(t) = x_0 e^{kt}$,而不是別的底數。
在 $RC$ 電路里,我們是從微分方程出發,用最基礎的積分與對數計算,順理成章地走到了 $e$,$e$ 不是"被選出來的",而是"被推出來的"。
八、結語:從一個小電路,看見自然的統一模式
$RC$ 放電電路看起來只是電路課上的一個小例題,但它實際上給我們展示了一個更大的事實:
- 只要系統滿足"變化率與當前值成比例",
- 微分方程就長得像一階系統;
- 積分就會引出 $\ln$,
- $\ln$ 的反函數就是以 $e$ 為底的指數函數。
$e$ 是自然界中描述"自我決定式變化"的最簡底數。
而 $RC$ 放電,只是這類系統中最簡單、最直觀、最容易親手做實驗驗證的一個例子。