此分類用於記錄吳恩達深度學習課程的學習筆記。
課程相關信息鏈接如下:
- 原課程視頻鏈接:[雙語字幕]吳恩達深度學習deeplearning.ai
- github課程資料,含課件與筆記:吳恩達深度學習教學資料
- 課程配套練習(中英)與答案:吳恩達深度學習課後習題與答案
本篇為第二課的第二週內容,2.8的內容,同時也是本週理論部分的最後一篇。
本週為第二課的第二週內容,和題目一樣,本週的重點是優化算法,即如何更好,更高效地更新參數幫助擬合的算法,還是離不開那句話:優化的本質是數學。
因此,在理解上,本週的難道要相對較高一些,公式的出現也會更加頻繁。
當然,我仍會補充一些更基礎的內容來讓理解的過程更絲滑一些。
本篇的內容關於Adam優化算法,是在之前的Momentum和RMSprop基礎上的集成算法。
1. Adam 優化算法
前面我們已經學過Momentum和RMSprop算法。
先回憶兩個算法的核心思想:
| 算法 | 解決問題 | 技術手段 |
|---|---|---|
| Momentum | 梯度方向不穩定、震盪 | 平滑梯度 |
| RMSprop | 梯度幅度差異大 | 平滑梯度平方、調節步長 |
在上一篇最後,我們提到,二者在使用上並不衝突,可以結合使用。
而結合後的方法同時應用平滑梯度和平滑梯度平方,實現平穩方向和自適應步長。
這就是Adam優化算法。
説實話,從原理上講,Adam基本就是把Momentum和RMSprop兩種算法加起來。
所以,只要能理解這兩種算法,那Adam的理解基本不是問題,我們直接展開Adam算法的公式邏輯。
1.1 Adam 的基本思想
Adam 會維護兩個量:
| 名稱 | 含義 | 對應哪部分算法? |
|---|---|---|
| 一階矩 vₜ | 平滑後的梯度(方向) | Momentum |
| 二階矩 Sₜ | 平滑後的梯度平方(幅度) | RMSProp |
也就是説:
- vₜ = 用來穩方向
- Sₜ = 用來調步長
Adam = vₜ + Sₜ 的協作更新。
1.2 一二階矩
(1)一階矩:平滑梯度 vₜ
來自Momentum,我們用 vₜ 表示平滑梯度:
這行的作用:平滑方向,避免梯度抖來抖去。
(2)二階矩:平滑梯度平方 Sₜ
來自RMSprop,用 Sₜ 表示平滑梯度平方:
這行的作用:感知“梯度大小的平均幅度”,用於自適應調步長。
1.3 一二階矩為什麼能起到相應作用?
再補充一點,你可能會有這樣一個問題:
為什麼用一階矩來平滑方向,用二階矩調節步長?這麼設置的合理性在哪?他們能換個位置嗎?
我們總地説一下梯度和梯度平方最大的區別:
- 梯度帶正負號,包含方向信息
- 梯度平方一定為正,體現的是“幅度”
現在再展開看一下:
| 角色 | 是否保留方向(正負) | 代表的意義 | 最適合的任務 | 為什麼不能反過來? |
|---|---|---|---|---|
| 一階矩 vₜ | 保留正負號 | 過去梯度的加權平均(趨勢/方向) | 按趨勢穩定方向 | vₜ 會為正或負,不代表“大小趨勢”,無法判斷步長是否應該縮放 |
| 二階矩 Sₜ | 永遠 ≥ 0(沒方向) | 梯度平方的平均(尺度/大小) | 按尺度自適應調步長 | Sₜ 沒有方向信息,無法告訴你“往左還是往右” |
總之,vₜ 和 Sₜ 的功能無法互換 —— 一個負責“走哪邊”,一個負責“走多快”。
因此,我們不可能讓速度決定方向,也不能讓方向負責踩油門。
1.4 一二階矩的偏差修正
因為 v₀ = 0、S₀ = 0,一開始偏小,所以 Adam 做偏差校正:
一階矩修正:
二階矩修正:
同樣是之前就講過的內容,我們用偏差修正來彌補EMA在初期偏小的情況,修正帶來的影響也會在後期分母無限接近1的情況下自動消失。
1.5 Adam參數更新公式
到了這一步,我們先看看之前兩種算法的更新公式:
首先是Momentum:
這裏,我們主要使用一階矩來形成“慣性”,抵消樣本參數的個性化特徵信息同時加強共性特徵信息來緩解“震盪”。如果你有些忘了為什麼會有這種效果,再看看之前的詳細解釋:Momentum
然後,我們又引入RMSprop:
這裏,我們主要使用二階矩來對每個參數實現“自適應學習率”,用平滑梯度平方測定梯度“幅度”並以此來縮小大梯度,放大小梯度。同樣,如果你有些遺忘,詳細的解釋在這裏:RMSprop
看這兩個算法的公式,有沒有發現,他們更改的位置完全不衝突?
- Momentum 把和學習率相乘的梯度改為平滑梯度。
- RMSprop 用平滑梯度的平方做開方當成梯度的分母。
就像之前説的,Adam 的參數更新公式相比創新,它更像合成:
很明顯,Adam 把上面兩者結合起來,同時應用一階矩和二階矩,既有穩定方向,又能自動調節不同參數的學習率。
還是打個比方:Momentum就像告訴往哪走的指南針,而RMSprop像告訴怎麼走的地圖,二者相加就成了Adam這個智能導航。
2. 自適應優化算法(Adaptive Optimization Algorithm)
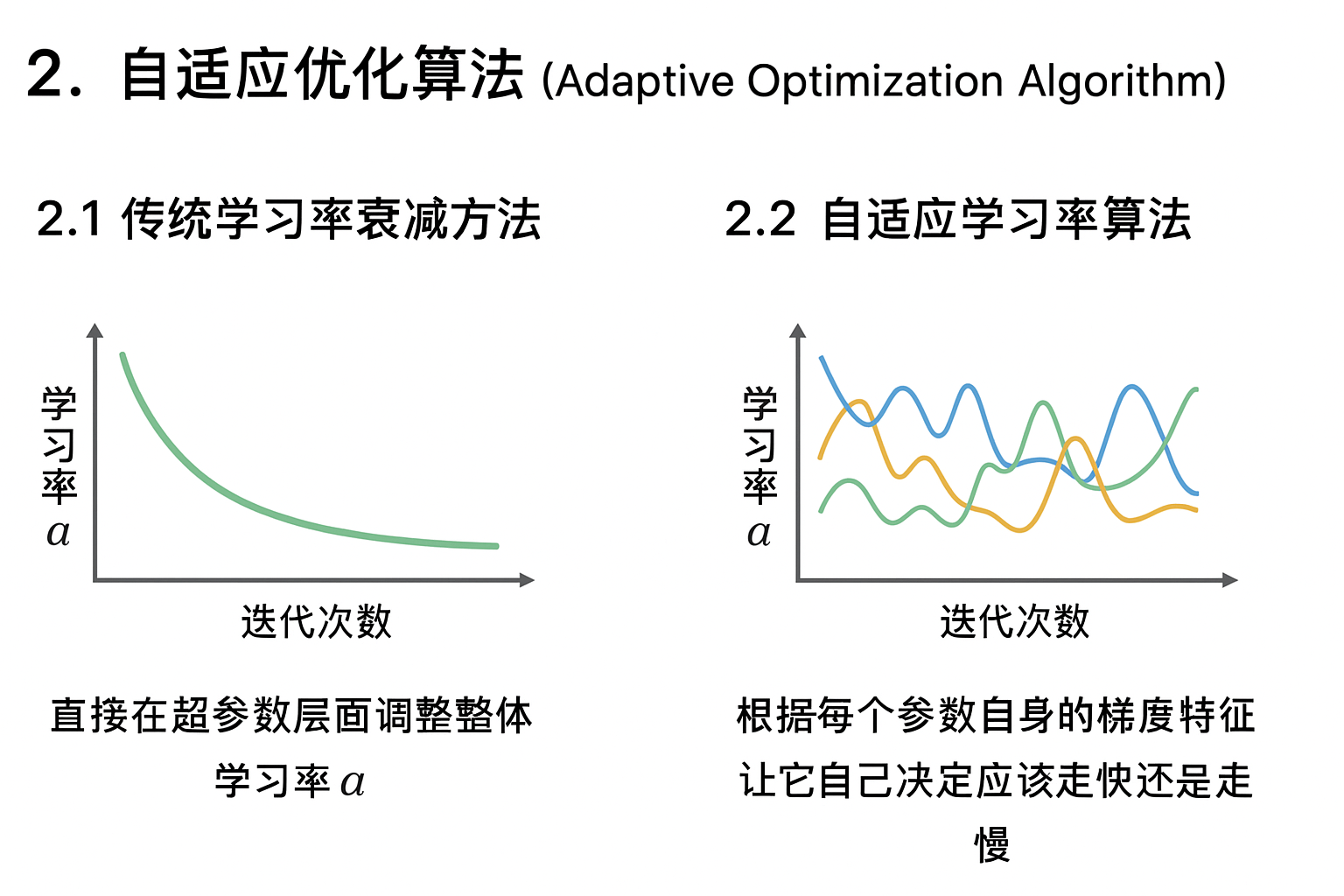
2.1傳統學習率衰減方法
我們在之前學習率衰減部分學過各種“學習率衰減”方法,比如 指數衰減、分段衰減、1/t 衰減 。
而這些方法的共同點是:直接在超參數層面調整整體學習率 α。
也就是説,它們的核心思路是:用一個全局函數控制所有參數的步長變化,每次迭代時整個模型的學習率一起變小或變大。
而我們也在RMSprop部分了解了這種對所有參數應用統一學習率的不足。
2.2 自適應學習率算法
實際上,RMSprop,Adam 算法被統稱為自適應學習率算法或者自適應優化算法。(還有一種叫AdaGrad,是改進前的RMSprop,幾乎不再使用,所以就不提了)
“自適應學習率(Adaptive Learning Rate)”指的並不是簡單地去改超參數 α, 而是根據每個參數自身的梯度特徵,讓它自己決定應該走快還是走慢。
換句話説,這類算法不是“直接改 α”, 而是“在更新時給每個參數都乘上一個自適應比例係數”。
從而形成一種 “隱式學習率” 的變化機制。
就像我們這兩篇所介紹的,這種機制讓算法能在不同維度上動態分配更新強度,即使學習率 α 是固定的,也能實現“局部自調節”的效果。
因此,Adam 不需要額外的衰減函數,也能自動學會該快時快、該慢時慢。
本週的理論部分就到此為止,下一篇的實操部分,我們就看看這些優化算法相比原來的普通梯度下降法,在性能上有多少提升。
3.“人話版”總結
| 概念 | 原理 | 比喻 |
|---|---|---|
| Adam | 同時計算一階矩(方向)和二階矩(幅度),並做偏差修正。綜合Momentum的“穩方向”和RMSprop的“調步長”。 | 像個智能導航系統:Momentum告訴你該往哪走,RMSprop告訴你怎麼走得穩,兩者合體成了“自動駕駛模式”。 |
| 傳統學習率衰減 | 通過全局公式(如指數衰減、1/t衰減等)手動讓整個模型學習率逐步下降。 | 像定時器:無論路況怎樣,到點就自動降速。 |
| 自適應學習率算法 | 不再改α本身,而是讓每個參數在更新時都帶上“自調節比例”,實現隱式學習率。 | 就像每個車輪都能獨立判斷地面情況,自主控制轉速,整體協調而智能地前進。 |