此分類用於記錄吳恩達深度學習課程的學習筆記。
課程相關信息鏈接如下:
- 原課程視頻鏈接:[雙語字幕]吳恩達深度學習deeplearning.ai
- github課程資料,含課件與筆記:吳恩達深度學習教學資料
- 課程配套練習(中英)與答案:吳恩達深度學習課後習題與答案
本篇為第四課的第一週內容,1.1到1.3的內容。
本週為第四課的第一週內容,這一課所有內容的中心只有一個:計算機視覺。應用在深度學習裏,就是專門用來進行圖學習的模型和技術,是在之前全連接基礎上的“特化”,也是相關專業裏的一個重要研究大類。
這一整節課都存在大量需要反覆理解的內容和機器學習、數學基礎。 因此我會盡可能的補足基礎,用比喻和實例來演示每個部分,從而幫助理解。
本篇的內容關於計算機視覺的入門知識:數字圖像處理
1. 什麼是計算機視覺?
簡單來説,計算機視覺(Computer Vision,CV)就是讓機器“看懂世界”。但“看懂”這件事,對人類來説像呼吸一樣自然,對機器來説卻非常不自然。
先來説説計算機是怎麼表示圖片的?
你可以把一張圖片想象成一張“巨型方格紙”。
每一個小格子裏都塞着一個數字,這個數字就是這個位置的亮度或顏色。
-
黑白圖片:一個格子一個數字
黑白圖最簡單,每個像素只有一個值,用來表示亮度。
舉個比喻,就像一幅“像素點拼成的黑白油畫”,每個點要麼黑一些、灰一些、亮一些。
電腦會把圖片變成一個 \(M \times N\) 的大表格,比如 \(28 \times 28\)。
表格裏每個數字範圍通常是 \(0 \sim 255\),代表亮度從黑到白。 -
彩色圖片:一個格子三個數字(RGB)
彩色圖片就像每個像素藏着三個小燈泡:
一個紅燈(R)、一個綠燈(G)、一個藍燈(B)。
三個燈的亮度不同,拼起來就成了各種顏色。
所以電腦會把一張彩色圖片存成一個 \(M \times N \times 3\) 的三維表格。
用比喻來説,就像把“彩色拼圖”拆成三張透明膠片:
第一張只畫紅色強弱、第二張畫綠色、第三張畫藍色,然後疊起來。
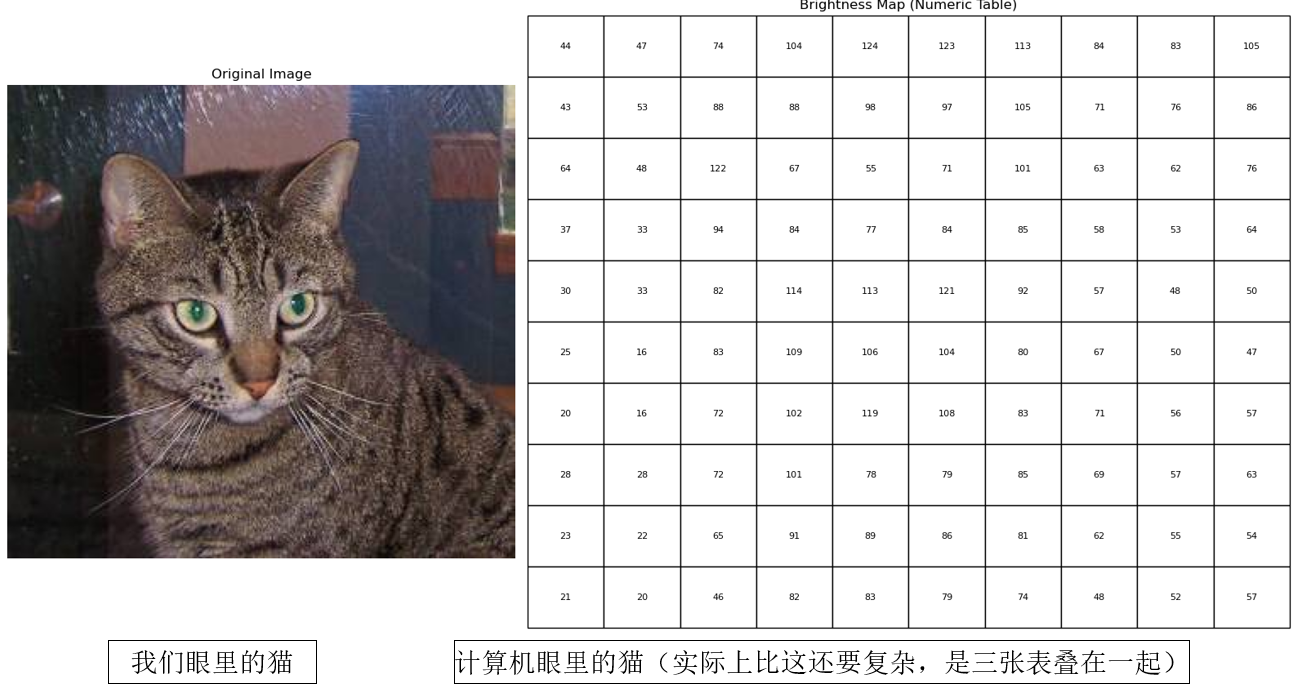
因此,無論人眼看到的圖像有多逼真、多可愛,對計算機來説最終就是:“一個大表格(矩陣),裏面每個格子寫着一些 0~255 的數字。”
舉個例子,我們看一張貓的照片,大腦裏有成千上萬條“經驗規則”,比如“圓圓的腦袋、尖尖耳朵、柔軟身體、鬍鬚”等等。孩子只要小時候見過幾次,就大致能認出來。
但機器沒有這樣的經驗,它看到的只是一個龐大的網格,其中每個格子裏一個或多個數字,意味着“這裏的亮度是多少”。
換句話説,對我們來説是一隻貓,對計算機來説是一張堆滿 0~255 的亮度數字的大表格。
而計算機視覺本質目的就是: 把這些冷冰冰的數字,變成機器能理解的“形狀、紋理、輪廓”等特徵。
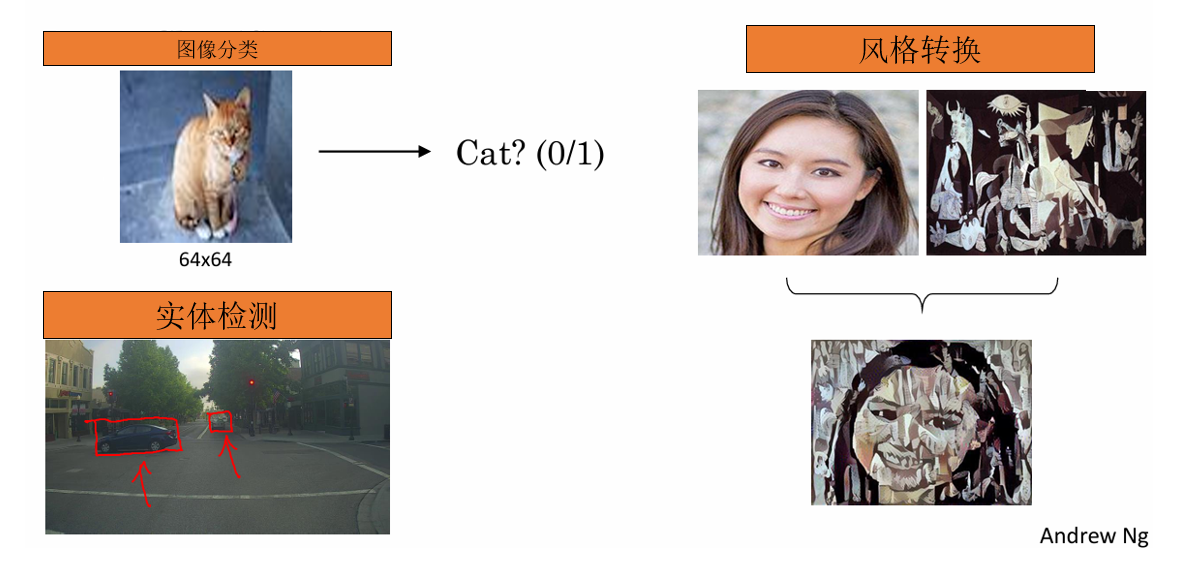
比如判斷“這是貓還是狗”“有沒有安全帽”“道路在哪”“有沒有缺陷”等等。
列舉一下課程中提到的幾個簡單的應用領域:
在瞭解了 CV 是用來幹什麼的之後,那又如何實現上面所説的“讓機器理解圖像”呢?
答案就是 CV 最常用的操作:卷積。
2. 全連接網絡做錯了什麼?
正式引入卷積之前,我們先看看,為什麼我們在 CV 不再繼續使用之前的的全連接網絡?
在上面我們裏我們説過,圖像在機器眼中,只是一張巨大無比的數字表格。那麼如果我們把這張表像之前一樣直接塞給之前學過的 全連接神經網絡 會發生什麼?
從理論上講,FC 確實能處理圖像,但它會做兩件非常“蠢”的事:
- 它把圖像當成一堆“孤立的數字”
比如一個 224×224 的圖片,全連接層會把它拉成一個 50176 維的長向量。
還記得我們之前在 FC 的的實踐模型的正向傳播中從沒強調過的第一步是什麼嗎? 是這個:
x = self.flatten(x) # 展平
這一步是在幹什麼?來看看:
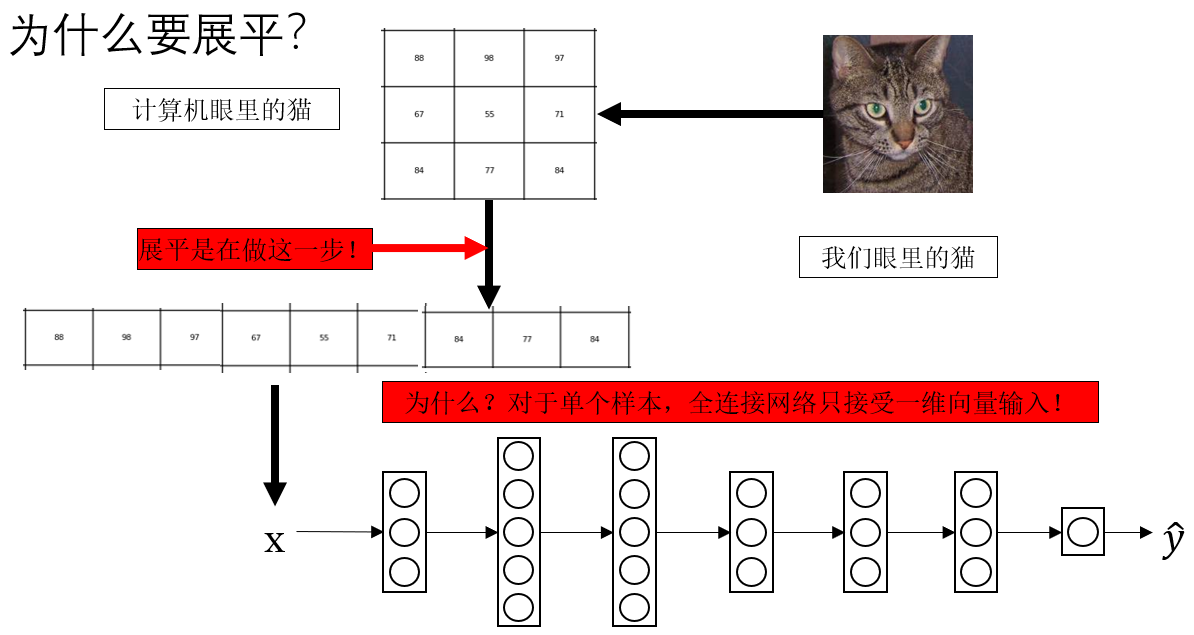
這就是展平的作用:為了符合 FC 的輸入要求,它把多維矩陣壓平成了一維向量。
但是這樣就會出現一個問題:
在它眼裏: “左上角的像素”和“右下角的像素”之間沒有任何關係,就是兩個數字。
但實際圖像不是這樣運作的。
我們用人類的直覺來打個比喻:
就像你隨便畫個小人,你也知道“眼睛在臉上”“鼻子不會跑到耳朵底下”,但對於壓平後的輸入,全連接網絡就不會認識到這一點。
因此,總結一下就是:圖像是有空間結構的,而 FC 會破壞這種結構。
- 全連接網絡的參數量會爆炸
一個 50176 → 1024 的全連接層,那他要維護參數量就是:
這麼恐怖的參數量,如果再多加幾層,模型直接炸掉,硬件也跑不動。
所以總結一下,全連接網絡在圖像任務上犯的兩個核心錯誤就是:
- 把圖像“拍扁”了,破壞了空間關係
- 參數量巨大,訓練困難、容易過擬合,硬件也帶不動。
如果説前一點是“腦子笨”,那麼後一點就是“身體差”。
為了彌補這些問題,我們需要一種“天然就擅長看圖”的方法,這個方法就是卷積。
3. 數字圖像處理:卷積(Convolution)
卷積是什麼?一句話概括:
卷積就是用一個小窗口在圖像上“滑來滑去”,並在每個位置做一次加權求和。
這個“小窗口”我們稱為卷積核(Filter 或 Kernel)。
你可以把它想象成一個小印章:
(1)把印章蓋在圖像某一塊
(2)圖像那塊區域與印章“點對點相乘再加起來”
(3)得到一個新的像素值
(4)挪到下一格
(5)重複
最終,整張圖就變成了一張“新圖”。
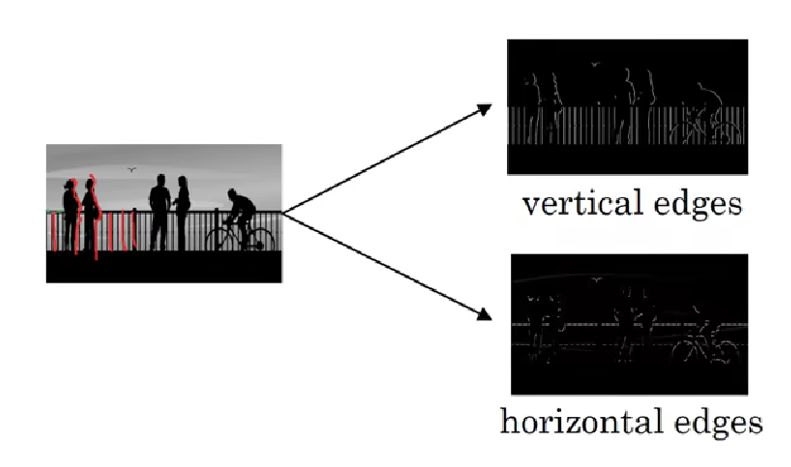
這麼説還是太抽象了,我們來做課程中的一個完整實例:邊緣檢測,實現下面這個效果:
我們一步步演示一下這個過程:
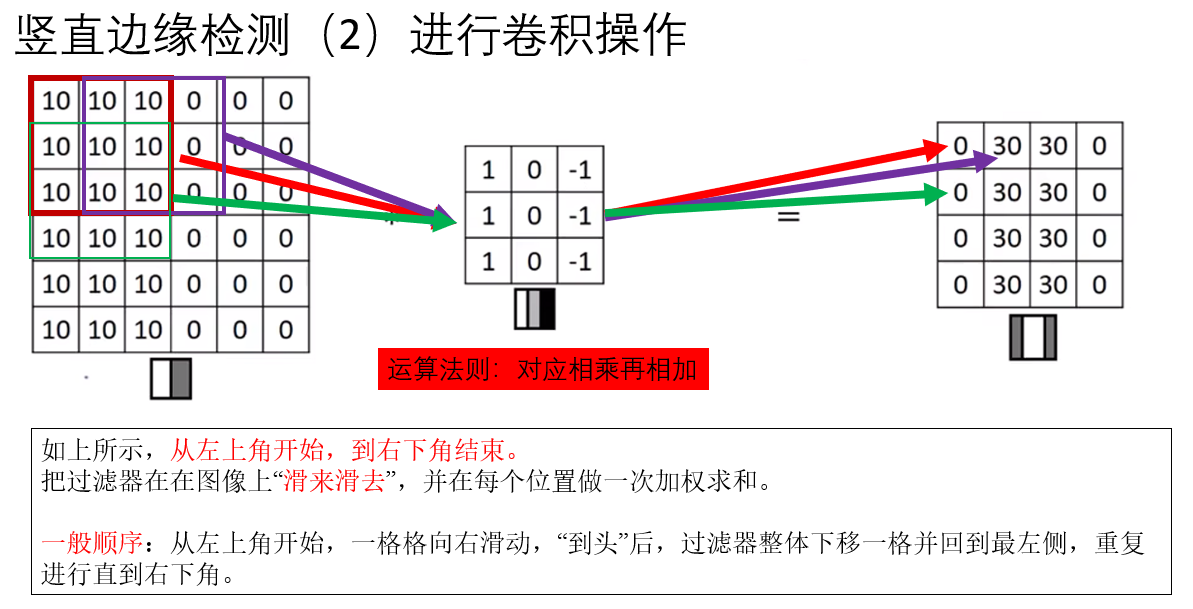
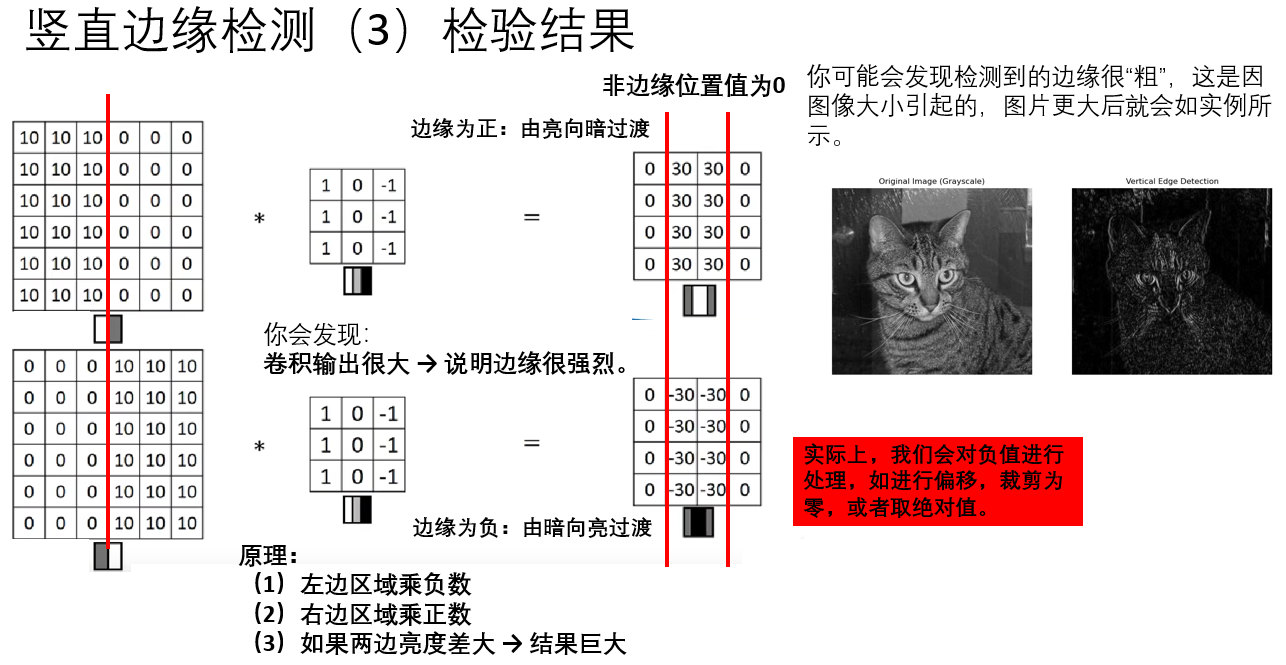
這就是整個卷積計算的過程和邊緣檢測的原理。
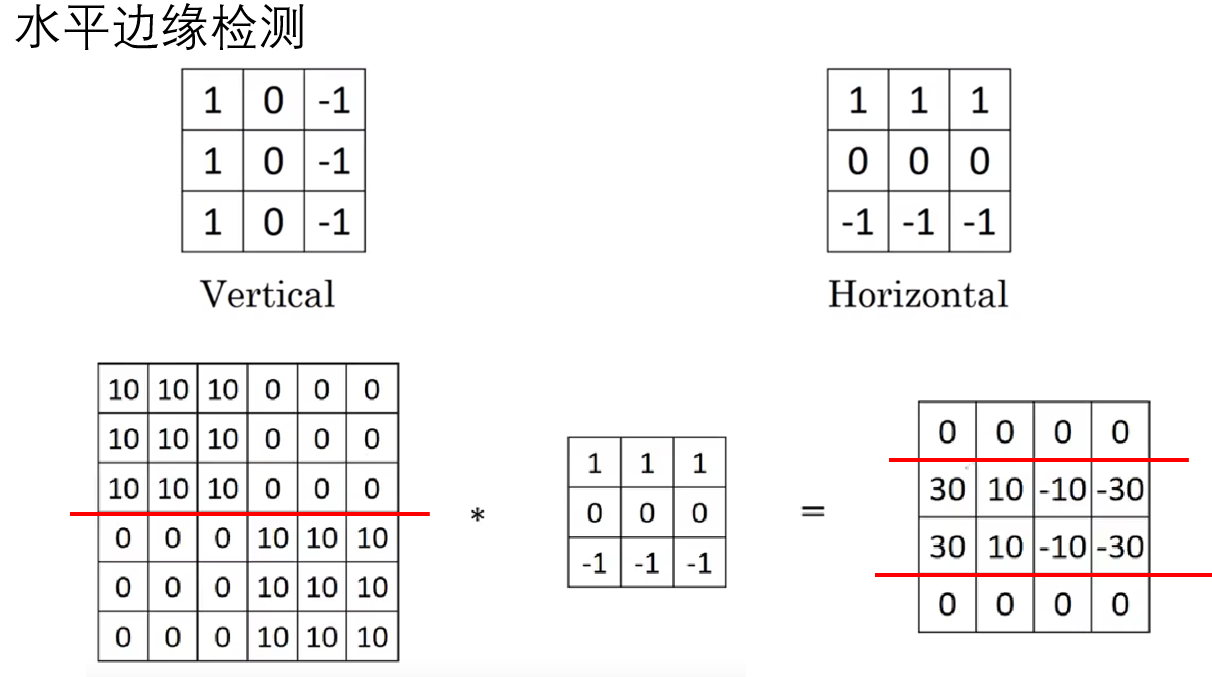
根據豎直邊緣檢測的原理,很容易就可以得出水平邊緣檢測的過濾器:
現在,我們只要使用這樣格式的過濾器對圖像進行卷積操作,就可以檢測圖像的邊緣。
最後一部分,我們按課程內容再對過濾器進行一些拓展。
4. 過濾器與卷積核
上面我們已經看到,過濾器(卷積核)本質上就是一個“帶着權重的印章”。
但在不同的領域,它會有兩個名字:
4.1 過濾器
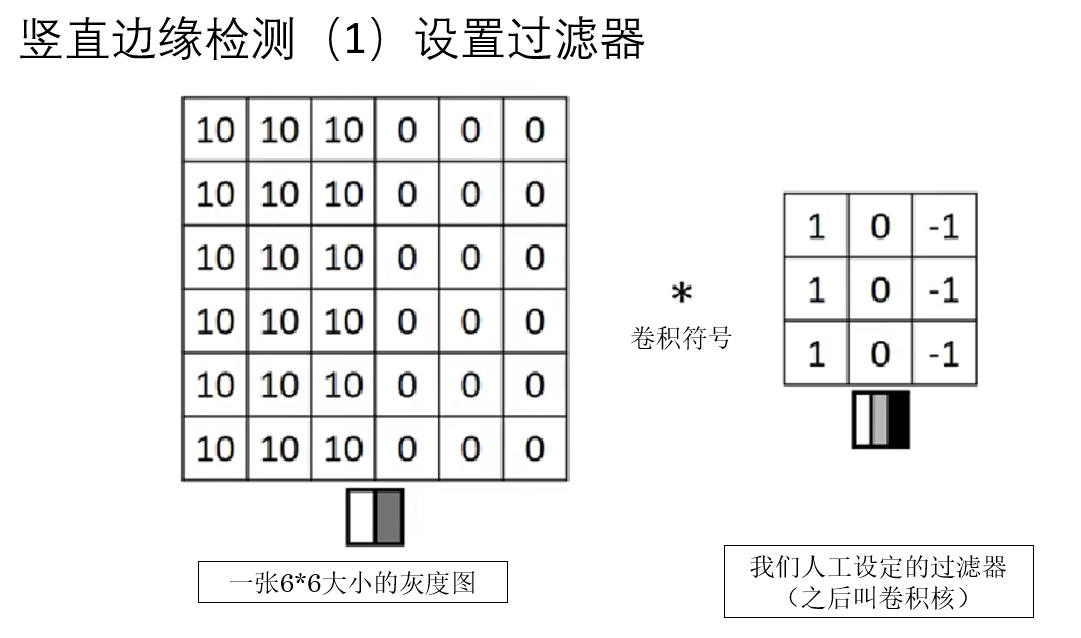
過濾器通常指 人工設計好的固定權重表,例如剛才做邊緣檢測用的豎直邊緣過濾器:
它不會變,就是死的、固定的,這種稱呼常用於數字圖像處理和信號處理中。
除此之外,在邊緣檢測中,我們還有一些經過檢驗和優化後的經典過濾器。
就像Adam相對於普通梯度下降一樣,我們簡單看一看:
(1) Sobel 過濾器(Sobel Filter)
Sobel 是比上面的的“簡單邊緣檢測過濾器”更常用、更平滑的一種。它在檢測邊緣的同時,也對鄰域進行了輕度平滑,使得檢測效果更穩定。
它的豎直邊緣檢測過濾器為:
水平方向檢測為:
你會發現它和簡單過濾器相比,中間那一列成了 \(2\),這樣做的效果是:
讓過濾器更關注中心區域,使得邊緣檢測更穩定、更抗噪聲。
(2) Scharr 過濾器(Scharr Filter)
Scharr 是 Sobel 的升級版,進一步增強了旋轉一致性。
簡單説,它比 Sobel 更“均勻”,更能在各種角度下檢測出穩定的邊緣。
它的豎直方向過濾器:
水平方向過濾器:
你可以看到 \(10\) 這個數字的出現,它相當於加強了方向性的權重。
當你需要更精確、更抗噪聲、角度更穩定的邊緣檢測時,用 Scharr。
最後來看看效果:

肉眼乍一看可能看不出太大的區別,但是在細微之處確實有相應的不同。
再來説説卷積核。
4.2 卷積核(Kernel)
在深度學習裏,這些權值不是人工設置的,而是通過梯度下降 自動學習出來的。
也就是説,每一組\(3\times 3\) 或 \(5\times 5\) 的權值,都像“模型在做作業時不斷寫、擦、修正筆記”,最終形成了能識別物體的特徵模式,在深度學習領域的卷積神經網絡裏,我們稱之為卷積核。
這一篇主要是關於圖像處理的一些基本知識,之後我們再慢慢展開在深度學習中卷積網絡的結構和應用等詳細內容。
5.總結
| 概念 | 原理 | 比喻 |
|---|---|---|
| 計算機視覺(CV) | 將圖像從“像素表格”轉換成模型能理解的結構化信息 | 像讓一個從未見過世界的孩子學會“看懂照片” |
| 全連接網絡處理圖像的缺點 | ① 展平破壞空間結構 ② 參數量巨大 \(50176\times1024\) | 把一張風景拆成一串數字,就像把一幅畫剪碎成紙屑很難拼回去 |
| 卷積(Convolution) | 用卷積核在圖上滑動,做“局部加權求和”,生成特徵圖 | 一個帶圖案的小印章不斷蓋在圖像各處 |
| 卷積核 / 過濾器 | 正方形的的權值表,用來提取局部特徵 | 換不同圖案的印章,就能蓋出不同風格的結果 |
| 邊緣檢測濾波器(基礎版) | 利用像 \([[1,0,-1],[1,0,-1],[1,0,-1]]\) 這種結構檢測垂直邊緣 | 數字版“照妖鏡”:亮暗對比越強,越容易顯形 |
| Sobel 過濾器 | 引入 \(2\) 的加權,使邊緣檢測更平滑、更抗噪聲 | “加強版照妖鏡”,能穩定看出對比度變化 |
| Scharr 過濾器 | 引入 \(10\) 加權,旋轉一致性更好,比 Sobel 更精確 | 角度再變,它也能穩穩抓住“哪裏變亮變暗” |
| 卷積核(深度學習版) | 權重由反向傳播自動學習,不再人工設計 | 像孩子自己總結“看到耳朵尖尖+圓腦袋=貓”的規則 |