此分類用於記錄吳恩達深度學習課程的學習筆記。
課程相關信息鏈接如下:
- 原課程視頻鏈接:[雙語字幕]吳恩達深度學習deeplearning.ai
- github課程資料,含課件與筆記:吳恩達深度學習教學資料
- 課程配套練習(中英)與答案:吳恩達深度學習課後習題與答案
本篇為第四課的第二週內容,2.5到2.7的內容。
本週為第四課的第二週內容,這一課所有內容的中心只有一個:計算機視覺。應用在深度學習裏,就是專門用來進行圖學習的模型和技術,是在之前全連接基礎上的“特化”,也是相關專業裏的一個重要研究大類。
這一整節課都存在大量需要反覆理解的內容和機器學習、數學基礎。 因此我會盡可能的補足基礎,用比喻和實例來演示每個部分,從而幫助理解。
第二週的內容是對一些經典網絡模型結構和原理的介紹,自然會涉及到相應的文獻論文。因此,我也會在相應的模型下附上提出該模型的論文鏈接。
本篇的內容關於 1×1卷積與Inception網絡。
1. 1×1卷積
1×1卷積的全稱是在卷積層中使用1×1大小的卷積核。
很顯然,乍一看這是一個讓人疑惑的設置——我們知道,卷積操作的作用就是提取局部特徵,而現在如果把卷積核設置為1×1大小,那不就是給輸入整個乘了一個係數嗎?有什麼用?
在2013年前,大部分人也都是這種想法,直到這一年,一篇名為Network in Network的論文被髮表,論文提出了 1×1 卷積可以在不改變特徵圖空間尺寸的前提下,對通道維度進行線性組合,從而靈活地調整通道數,並通過疊加非線性顯著提升網絡表達能力;相比用大卷積核堆疊實現相同效果,其參數量和計算量都更低。
因此,1×1 卷積雖然不能像其他卷積核一樣用來提取局部特徵,但它也有自己獨特的作用。
用更好理解的話來説,1×1 卷積像是 “通道數上的池化(但帶參數、還能升維)”和“卷積實現的全連接” 。
不太明白很正常,下面我們就來展開敍述。
1.1 1×1 卷積的實質:通道維度上的線性組合
我們已經知道,1×1 卷積不能用來提取空間上的局部特徵。
在實際運算中,它做的事情非常單一:在每一個空間位置上,對所有通道對應的數值做一次線性組合。
説到這裏,你可能會感到有些熟悉——這種運算形式,好像在某個地方已經見過了。
我們先來看課程中的這個例子:
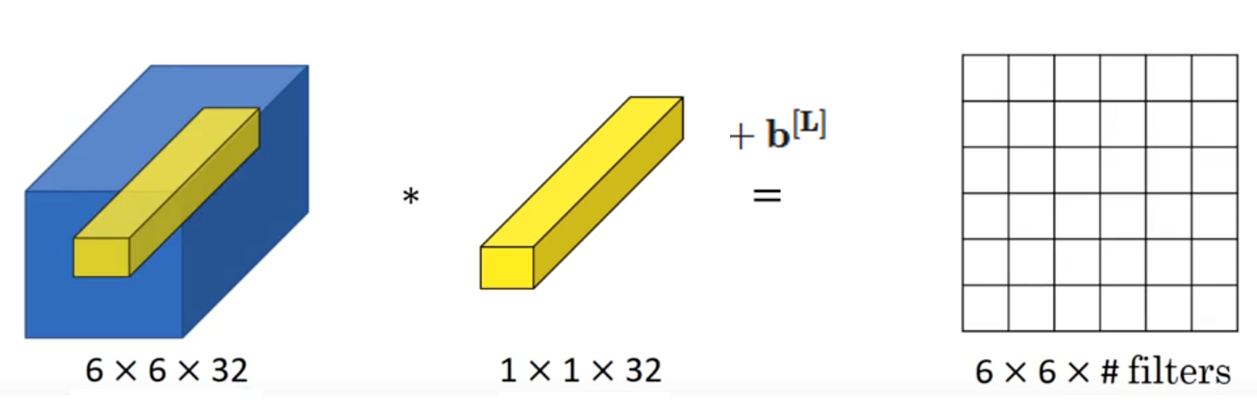
如果用數學形式來表示這一次的計算,就是這樣:
沒錯,這就是單個樣本在全連接層的線性組合公式。
在這個例子裏,可以這樣理解:
- 對於特徵圖中的每一個空間位置。
- 該位置在 32 個通道上的數值,組成了一個 32 維向量。
- 1×1 卷積所做的,就是對這個 32 維向量進行一次線性組合,得到新的輸出特徵。
從這個角度來看,每一個空間位置都可以被視作一個“獨立的小樣本”,而 1×1 卷積在該位置上的作用,就等價於對這個樣本做了一次全連接層的計算。
所以説:1×1 卷積本質上是在同一空間位置上對通道做線性組合。
我們繼續,還記得我們在卷積層特點裏提到過的參數共享嗎?
正是由於同一組 1×1 卷積核會共享到所有空間位置,網絡會在反向傳播過程中不斷調整這些權重,從而學會:
- 哪些通道對應的特徵更重要。
- 哪些特徵應該被弱化。
- 哪些特徵可以通過線性組合整合成更有效的表示。
我們再舉一個簡單的示例看看:
假設在某一層網絡中,某一個空間位置 \((i,j)\) 在 3 個通道上的取值分別是:
這表示:在同一空間位置上,三個通道對應的特徵值分別為 \(2\)、\(1\) 和 \(-1\)。
現在,我們對這一層使用 1×1 卷積,設該卷積核在通道維度上的權重為:
那麼,該位置的線性組合結果為:
如果我們使用多個 1×1 卷積核,那麼同一個位置就可以輸出多個這樣的數值,從而得到新的多通道特徵圖。
在瞭解了原理後,我們來看看1×1卷積在實際中更常見的一種應用。
1.2 使用1×1卷積調整通道數
使用1×1卷積,在保持空間尺寸不變的前提下,對通道數進行調整,減少計算量。這才是它在實際設計中更常見的應用。
其中一個原因是因為在實際調試中,我們很難直接感受網絡的非線性和表達能力的強弱,但是卻能直接地測算出網絡參數量和計算量的減少。
另外就是一些特殊的網絡需要通道數的對齊,比如殘差網絡,我們很快就會提到它。
來看課程中這樣一個例子:
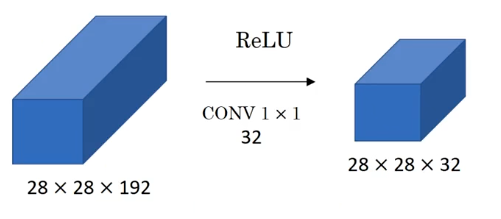
可以看到,這一層卷積僅僅改變了通道數的大小,為什麼要這麼做?
我們知道,如果想在不增加太多參數的情況下壓縮特徵圖的空間尺寸,池化通常是一個常用的選擇。
我們打幾個比方來幫助理解:
可以把池化理解為“把一張高清照片縮小分辨率”:畫面變小了,細節少了一點,但整體輪廓還在。
但池化有一個明顯的侷限:它只能壓縮長和寬,卻無法改變通道數。
也就是説,池化只能讓“每一張圖變小”,卻沒法決定“這組圖裏到底保留幾張”。
因此,當我們希望在保持空間尺寸不變的前提下,對通道數進行調整時,就不得不引入卷積操作。如果直接使用 3×3、5×5 這樣的卷積核,就相當於一邊在做空間特徵提取,一邊還要完成通道重組,參數量和計算量都會迅速增加,而現在我們只想調整通道數。
在這種情況下,1×1 卷積就像一個“通道維度上的判斷者”。
它不會去看周圍像素的信息(實際上也看不了),而是站在每一個空間位置上,只對該位置的所有通道做重新組合:哪些特徵該保留,哪些該弱化,哪些可以合併在一起,都由 1×1 卷積來決定。
因為就像上面所提的: 1×1 卷積本質上是在同一空間位置上對通道做線性組合。
總結一下,1×1 卷積不負責“看得更廣”,而是負責“把已有的信息整理得更清楚”,即在不改變空間結構的前提下,對特徵進行重組與篩選。
正因為它不引入新的空間鄰域關係,卻又能靈活調整通道數,所以相比使用大尺寸卷積核,它在完成相同通道變換任務時,參數量和計算開銷都要小得多。
1.3 拓展:ResNet 中的 1×1 卷積應用
在上一篇殘差網絡中我們就提到過,ResNet 中有很多細節值得説明,對 1×1 卷積的使用就是其中之一。
這裏我們正式引入1×1 卷積後,就再來看看它在 ResNet 中發揮的作用。
再複製一下殘差網絡中的一個關鍵點:在殘差塊中,參與融合(相加)的兩條分支,其輸出張量的維度必須一致,否則殘差相加無法進行。
ResNet 裏有那麼多殘差塊,總不能讓數據在傳播中全設置為固定維度吧?
1×1 卷積正是 ResNet 中解決這一問題的關鍵工具,它在 ResNet 既起到了維度對齊的作用,又在深層網絡中減少了計算量。
下面就簡單展開一下:
(1)用於殘差分支中的“維度對齊”
我們已經知道,殘差連接的核心操作是:
但是再重複一遍,這裏有一個隱含前提:\(F(x)\) 和 \(x\) 的 形狀必須完全一致(空間尺寸 + 通道數)。
在理想情況下,殘差塊輸入輸出通道數相同,旁路連接可以直接相加;但在實際網絡設計中,經常會遇到這種情況:
- 主分支通過卷積 改變了通道數(例如 64 → 128)。
- 或者通過 stride=2 的卷積 改變了空間尺寸。
這時,原始輸入 \(x\) 已經無法直接與 \(F(x)\) 相加。
而解決方法就是:
在旁路上引入一個 1×1 卷積,對 \(x\) 做一次線性映射:
再進行殘差相加:
這裏有一點很容易迷惑:我記得1×1 卷積不是隻能改變通道數嗎?它怎麼適應空間尺寸的變化?
別忘了,卷積有好幾個超參數呢:
我們可以通過調整 1×1 卷積步長和 padding 讓他適應 \(F(x)\) 的尺度。
打個比方來總結一下: 這裏的 1×1 卷積就像一個轉接頭,讓旁路連接能順利進行。
(2)用於 Bottleneck 結構中的“降維—升維”
論文在更深的 ResNet(如 ResNet-50 / 101)中,引入了著名的 Bottleneck 結構:
這裏的兩個 1×1 卷積並不是為了提取空間特徵,而是承擔通道調度的作用:
- 第一個 1×1 卷積:降維,減少通道數,降低後續 3×3 卷積的計算量。
- 第二個 1×1 卷積:升維,恢復通道數,保證與殘差分支可相加。
為什麼要這麼做?
還是打個比方:
如果把 3×3 卷積看成是“需要對每一個像素周圍反覆計算的大型加工機器”,那麼 1×1 卷積更像是一個“預處理與整理工序”:
- 幹活前,先用 1×1 卷積把原本“雜亂、冗餘、維度很高”的原材料壓縮成更精簡的形態(降維),讓後續的 3×3 卷積在更少的通道上重複計算;
- 幹活後,再用 1×1 卷積把加工後的結果重新展開、整合成需要的規模(升維)。
這樣做的關鍵在於:把最耗計算量的 3×3 卷積,限制在更小的通道空間裏執行。
而這樣做的結果是:
相比三個3×3 卷積,在幾乎不損失表達能力的前提下,大幅降低參數量和計算量。這是 ResNet 能夠做到“又深又能訓”的重要原因之一。
而這裏的 1×1 卷積不直接創造新信息,但決定信息如何高效、順暢地流動。
這便是 ResNet 對1×1 卷積的應用。
2. Inception網絡
在開始之前,需要先説明的是:Inception 網絡不同於 ResNet,其完整結構在當前主流視覺模型中已較少直接使用,尤其是在 Transformer 架構興起之後,其整體設計思路逐漸淡出主流。
因此,這裏不再對 Inception 網絡本身展開過多細節,而是主要説説它的一項至今仍被廣泛借鑑的一項核心思想——多尺度卷積。
2.1 多尺度卷積
我們已經瞭解了很多卷積網絡了,如果再讓我們自己設計卷積網絡,你更傾向先設置卷積核為多少?
我個人更傾向於使用一些著名論文裏的參數設置,再進行調試看看效果,但這樣又花費了大量的時間。
因此,在 2014 年,一篇名為 Going deeper with convolutions的論文提出了這樣一個想法:不知道哪個好那我就都用上,即不再人為固定卷積核尺度,而是在同一層中並行使用多種不同大小的卷積核,讓網絡在訓練過程中自動學習如何組合和利用不同尺度的特徵。
具體是怎麼進行的?來看看課程裏的示例:
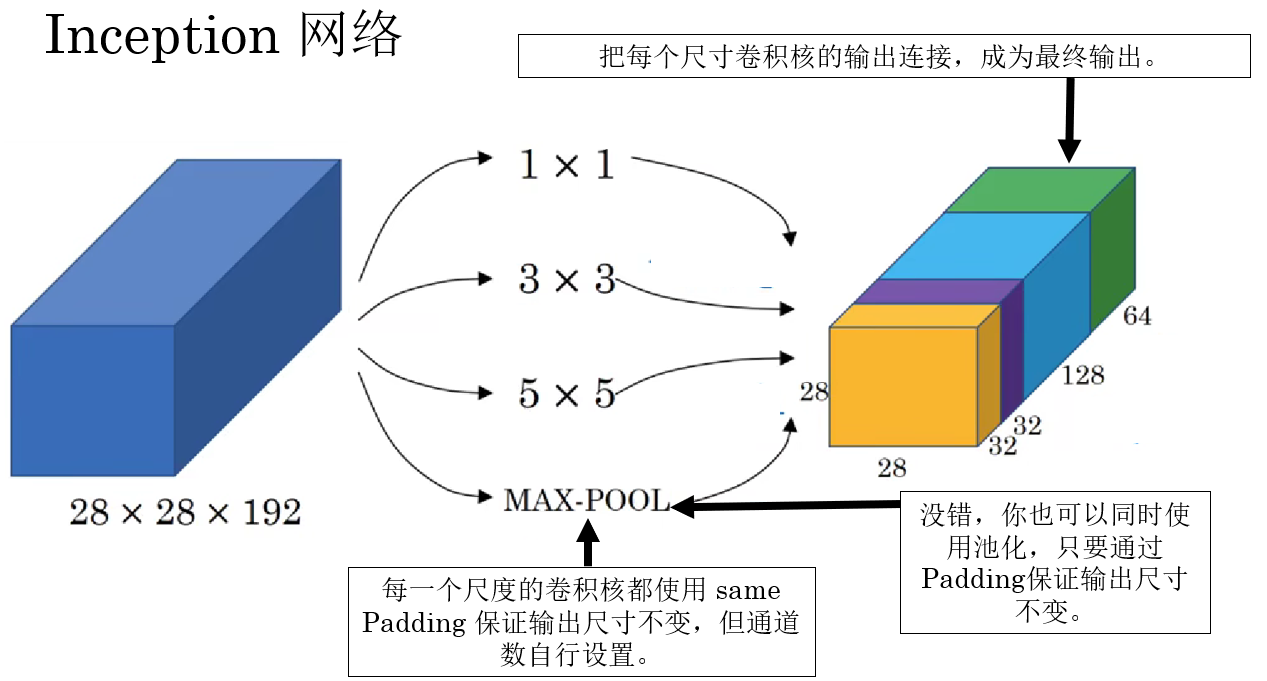
這一設計在當時確實達成了性能的提升,但同時也帶來新的問題:極大的參數和計算量。
我們繼續:
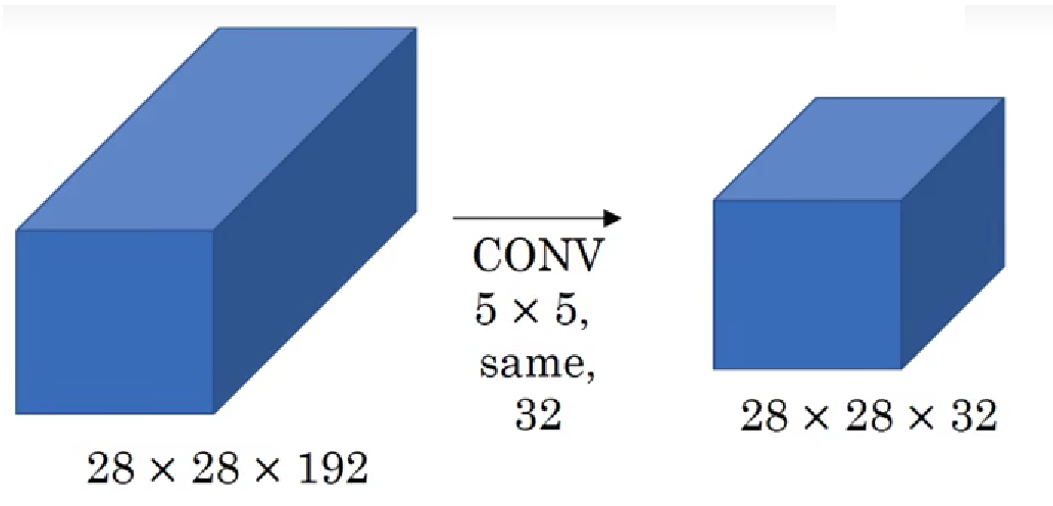
直接説結論:這層的正向傳播會經過 1.2 億次乘法運算, 這還只是網絡中的一層。
那如何減少計算量?沒錯,Inception也應用了1×1 卷積。
2.2 Inception的1×1 卷積應用
實際上也很簡單,把剛剛的層級結構改成下面這樣:
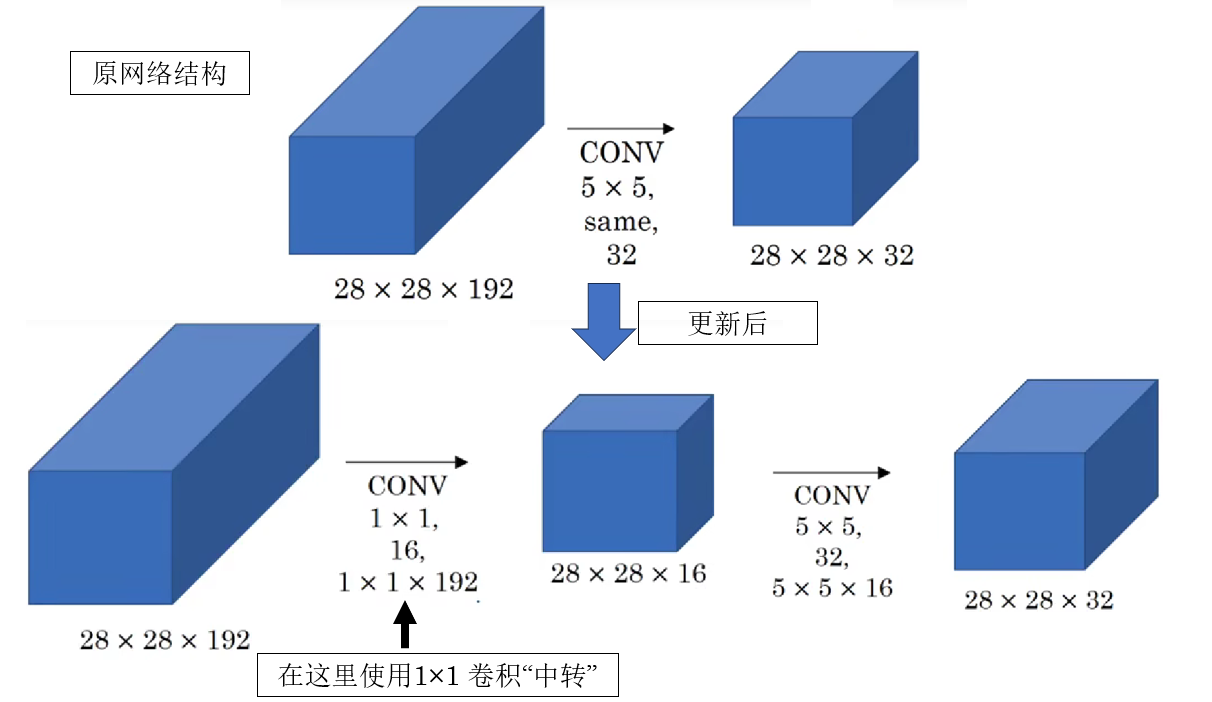
現在,這兩次卷積運算也只會使用 1240 萬次乘法,是原本的十分之一。
原理很簡單:之前使用 32 個 5×5 卷積核直接對輸入進行卷積,而現在在對輸入進行卷積前,我們先用 1×1 卷積把輸入通道數先壓縮到原來的十分之一量級,總體上減少了計算量。
就不再詳細展開計算過程了。
因此,下面就看看引入1×1 卷積後,Inception對一次多尺度卷積的設計是什麼樣的。
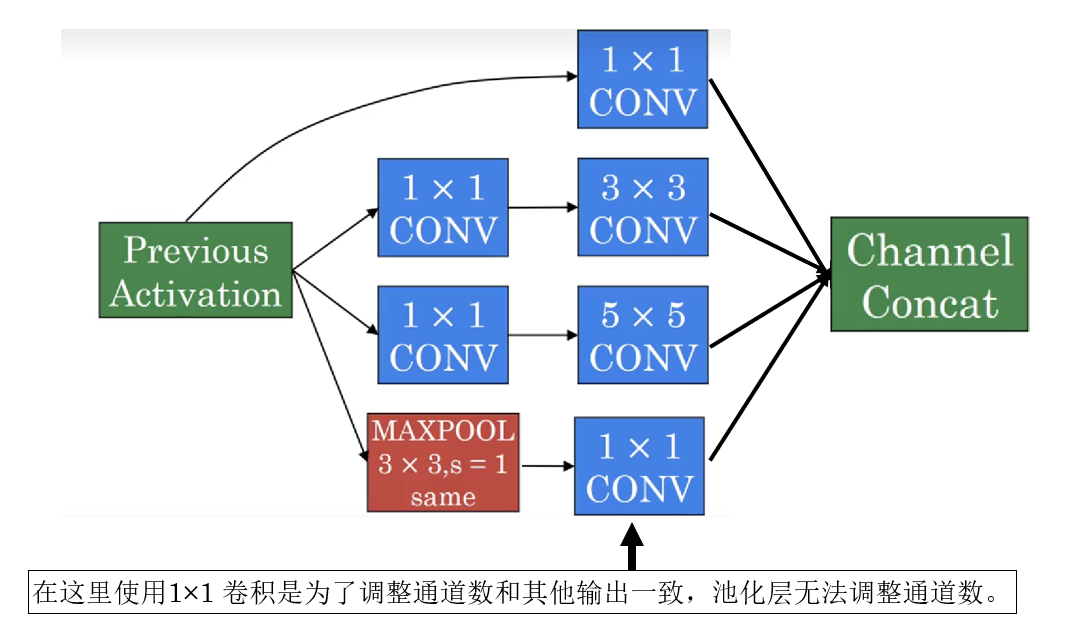
2.3 Inception的網絡結構
對於每層來説,實際上是就是給大尺度卷積核前都使用了一次1×1 卷積,像這樣:
而整個網絡就是這樣層級的堆疊:
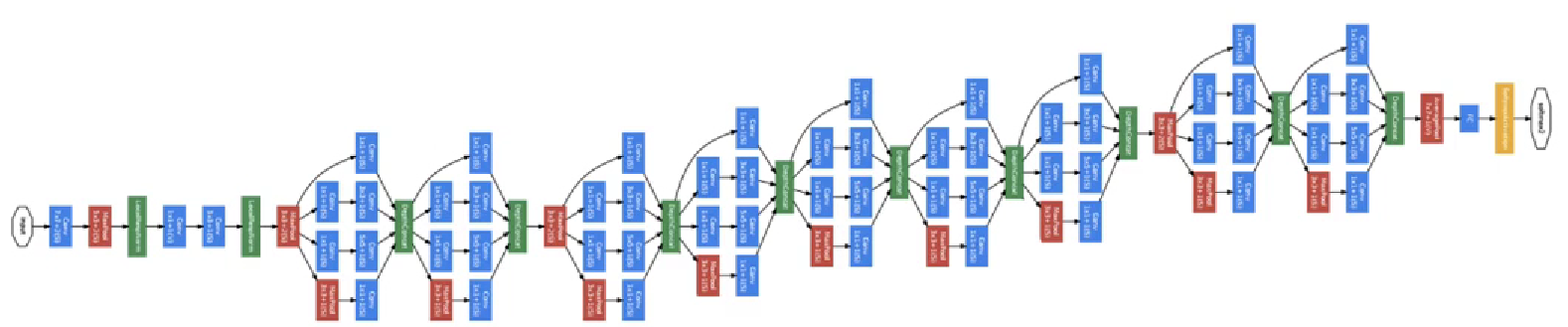
就不再過多展開關於 Inception 的內容了。
雖然 Inception 本身已經近乎退場,但他的貢獻並不在於某一個具體模塊,而在於它第一次系統性地提出:單一尺度不足以描述複雜視覺結構。
後續模型幾乎無一例外地繼承了這一思想,只是將“多尺度”的實現方式,從同層並行卷積,演化為跨層結構、感受野調控或注意力機制。
3.總結
| 概念 | 原理 | 比喻 |
|---|---|---|
| 1×1 卷積 | 在不改變空間尺寸的前提下,對同一空間位置的通道向量做線性組合,可實現通道壓縮、擴展與重組 | 像是在每個像素點上做一次“帶參數的篩選與加權彙總”,不看周圍,只整理自己手裏的信息 |
| 通道調整(降維 / 升維) | 通過控制輸出通道數,減少或擴展特徵表示,尤其用於控制計算量 | 像是在決定:這批信息裏哪些值得繼續加工,哪些先壓縮收納 |
| 1×1 卷積 vs 池化 | 池化壓縮空間尺寸但不改通道;1×1 卷積改通道但不動空間 | 池化像縮小照片分辨率;1×1 卷積像整理照片冊裏保留幾張照片 |
| ResNet 中的維度對齊 | 當主分支改變通道數或空間尺寸時,用帶 stride 的 1×1 卷積調整旁路形狀以便相加 | 像一個轉接頭,把不匹配的接口接成能插上的形狀 |
| Bottleneck 結構 | 用 1×1 降維 → 3×3 計算 → 1×1 升維,把高成本計算限制在低維空間 | 像是先把原料切細再加工,最後再拼裝回成品 |
| Inception 的多尺度思想 | 同一層並行使用多種卷積核尺度,讓網絡自動選擇有效尺度 | 像是同時用放大鏡、普通鏡和望遠鏡觀察同一物體 |
| Inception 的計算問題 | 多尺度並行帶來參數和計算量爆炸 | 像是所有機器同時全速運轉,成本急劇上升 |
| Inception 中的 1×1 卷積 | 在大卷積前先壓縮通道,顯著降低後續多尺度卷積的計算量 | 像是先精簡原料,再送進重型加工設備 |

