此分類用於記錄吳恩達深度學習課程的學習筆記。
課程相關信息鏈接如下:
- 原課程視頻鏈接:[雙語字幕]吳恩達深度學習deeplearning.ai
- github課程資料,含課件與筆記:吳恩達深度學習教學資料
- 課程配套練習(中英)與答案:吳恩達深度學習課後習題與答案
本篇為第五課的第二週內容,2.1和2.3的內容以及一些基礎的補充。
本週為第五課的第二週內容,與 CV 相對應的,這一課所有內容的中心只有一個:自然語言處理(Natural Language Processing,NLP)。
應用在深度學習裏,它是專門用來進行文本與序列信息建模的模型和技術,本質上是在全連接網絡與統計語言模型基礎上的一次“結構化特化”,也是人工智能中最貼近人類思維表達方式的重要研究方向之一。
這一整節課同樣涉及大量需要反覆消化的內容,橫跨機器學習、概率統計、線性代數以及語言學直覺。
語言不像圖像那樣“直觀可見”,更多是抽象符號與上下文關係的組合,因此理解門檻反而更高。
因此,我同樣會儘量補足必要的背景知識,儘可能用比喻和實例降低理解難度。
本週的內容關於詞嵌入,是一種相對於獨熱編碼,更能保留語義信息的文本編碼方式。通過詞嵌入,模型不再只是“記住”詞本身,而是能夠基於語義關係進行泛化,在一定程度上實現類似“舉一反三”的效果。詞嵌入是 NLP 領域中最重要的基礎技術之一。
本篇的內容關於詞彙表徵和類比推理,是詞嵌入中的基礎內容。
1.詞彙表徵
先用一句話簡單概括一下:詞彙表徵的含義是將詞彙表示為多維特徵向量,以便模型對詞語進行計算與比較。
這也是詞嵌入方法所遵循的核心思想之一,下面就來詳細展開:
1.1 獨熱編碼在序列編碼中的侷限
在上週的引入中,我們就對獨熱編碼在序列編碼中的一些侷限有所提及,再簡單重複一下:獨熱向量的維度極高、且極度稀疏帶來了極高的存儲和計算成本,這一問題在詞典規模越大的任務中便越被凸顯。
但我們知道,這種成本上的問題往往並不是根本問題所在,有時甚至可以忽略,我們關注一門技術好不好,更多的是在乎它的“效益”,也就是對最終性能的提升。
因此,在序列信息的表示上,獨熱編碼的核心侷限並非成本,而是它限制了文本的語義表示,無法顯式建模詞語之間的語義關係。
這點並不難理解,我們用課程裏的例子來説明一下:
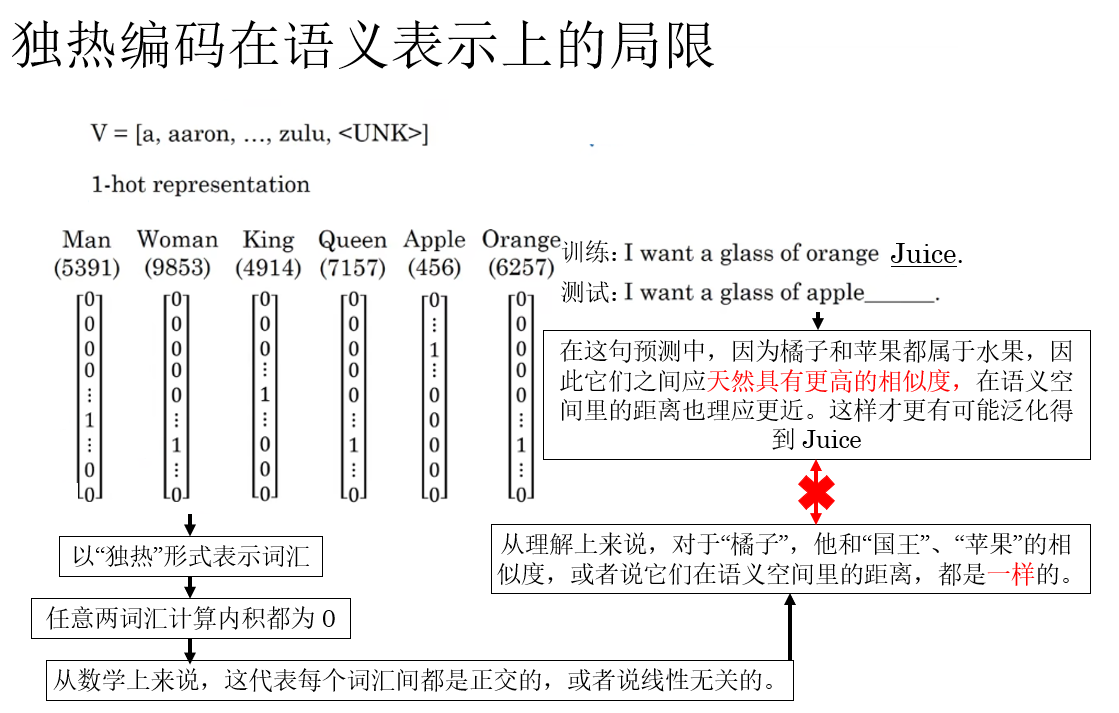
就像圖裏所示,換句話來總結:獨熱編碼將各個詞彙“孤立”了,斷絕了蘋果和橘子、父親和母親、男人和女人這樣的詞彙間的聯繫。
顯然,這對模型泛化能力的影響是極大的,這也是獨熱編碼在序列表示中的核心問題所在。
這個問題的解決方法就是使用詞彙表徵。
1.2 詞彙的特徵化表示
這點同樣很符合我們的語言直覺,既然我們知道各個詞彙間存在共性、存在某些維度上的相似,那就像歸納總結把它們列舉出來,就像這樣:
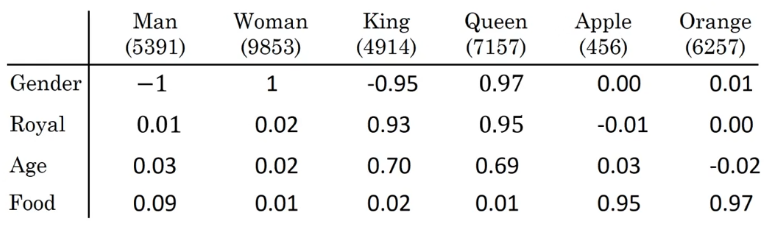
但是,這裏要專門強調一點:這些特徵不是我們人為手工定義的,我們這裏只是以此進行演示。在實際運行中,詞彙在各個維度上的值是通過相應的網絡學習並輸出的,其各個維度上的語義並不具備這樣較強的可解釋性。
在之後我們也會詳細展開相關內容。
在這一部分,吳恩達老師還提及了一種算法:t-SNE 算法,這種算法是一種把高維向量“攤平”到 2D / 3D 平面上,並儘量保留“局部相似關係”的可視化方法,我們可以以此來可視化各個詞彙在向量空間中的大致距離,就像這樣:
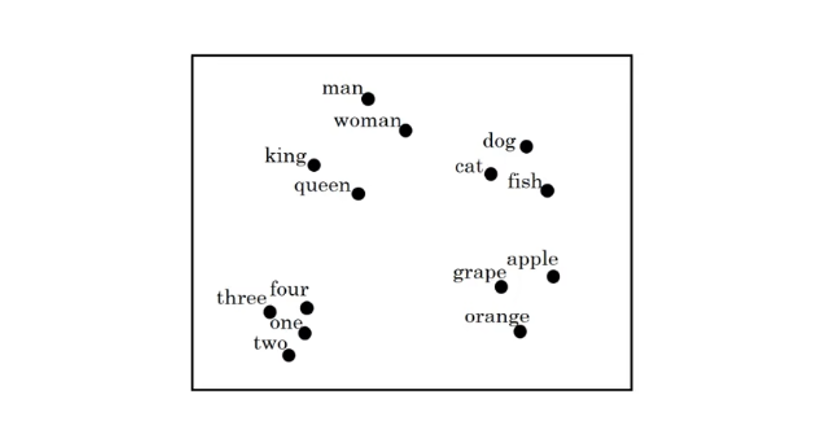
這個算法的原理涉及到很多沒提到過的數學概念,詳細介紹需要大量篇幅,而且目前也有了很多理論更優的同類型方法,因此就不在這裏展開了,以後如果有機會再專門介紹這類內容,這裏附上原論文鏈接:Visualizing Data using t‑SNE
最終,通過一個詞彙在多個維度上的表示,我們就通過另一種方式實現了對詞彙的編碼。
這種表示方式能夠通過向量間的距離度量詞彙語義相似性,從而提升模型的理解與泛化能力,同時也避免了獨熱編碼維度過高且表示稀疏的問題。
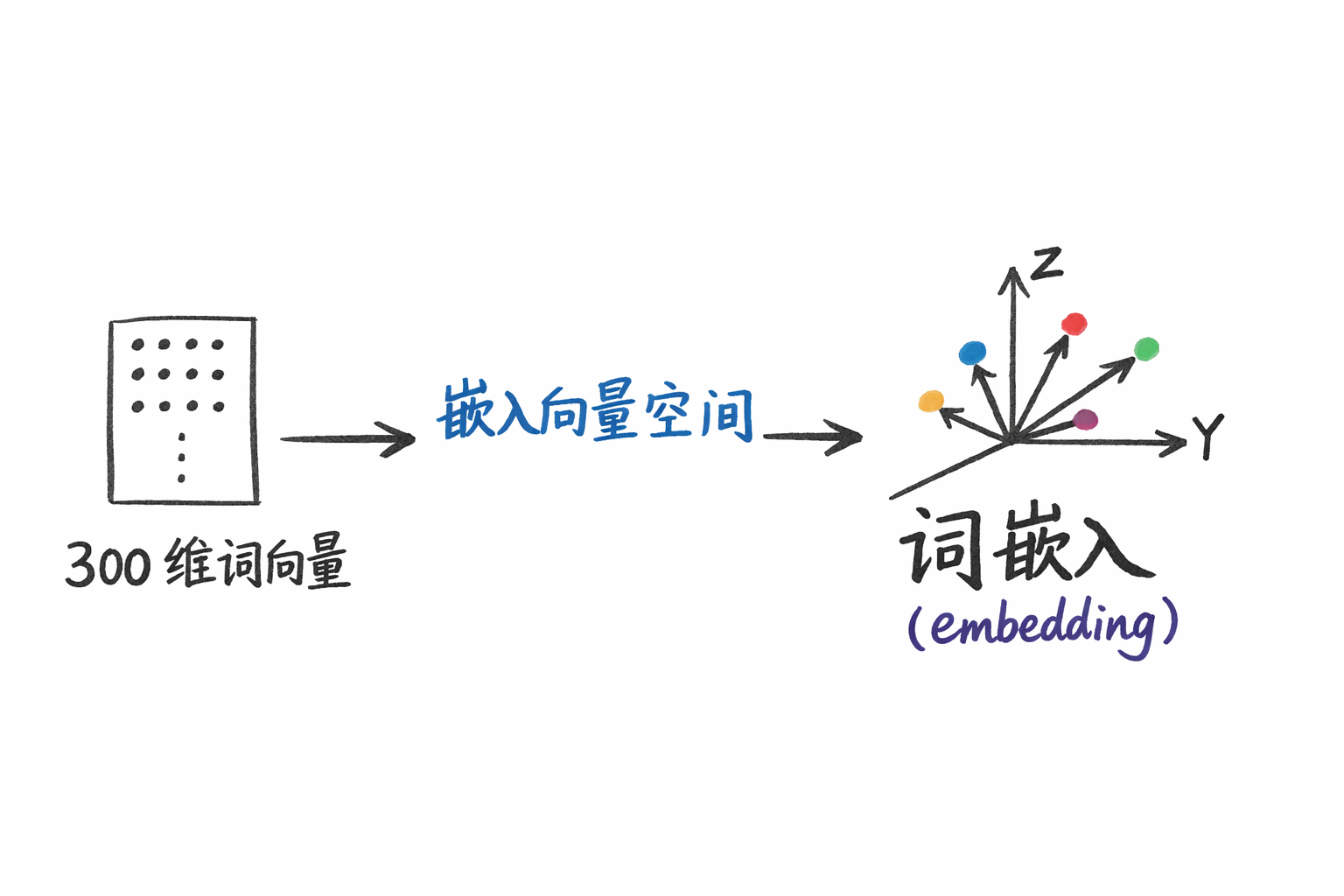
假設我們規定使用 300 維的特徵向量來編碼詞彙時,我們便稱這個特徵向量為詞向量。
同時,這樣一個個詞向量就像是“嵌入”在了這樣一個 300 維的向量空間裏。所以,當我們將詞彙表示為低維連續向量,並將其映射到同一向量空間中進行學習與比較時,這種表示方式就被稱為詞嵌入(embedding)。
我們之後就會詳細展開實現詞嵌入相關的技術和模型。
下面我們簡單展開一下詞嵌入實現的另一項應用:類比推理。
2. 使用詞嵌入進行類比推理
在我們實現了詞嵌入,得到詞表中詞彙的詞向量表示後,我們可以通過一種方式來觀察和驗證詞嵌入的語義能力,就是類比推理。
在 2013年,一篇名為Linguistic Regularities in Continuous Space Word Representations的論文就詳細展示了詞向量能反映語言類比現象的數據分析方法,同時,我們之後要介紹的 Word2Vec 中也展示了詞向量可以實現類比推理。
總之,詞嵌入中的類比推理通過向量運算驗證和展示詞向量的語義規律性,既體現了詞嵌入空間的線性結構,也能直觀反映模型對語言關係的理解能力。
同樣用一句話簡單概括一下:類比推理就是通過向量運算髮現詞彙間語義關係,比如“國王–男人+女人≈王后”。
公式表示為:
這是因為詞嵌入向量空間可以捕捉語義方向,而同類關係的向量差幾乎平行,因此通過向量運算就可以“舉一反三”,我們便可以由此驗證詞嵌入的語義能力是否合理。
簡單展開一下:
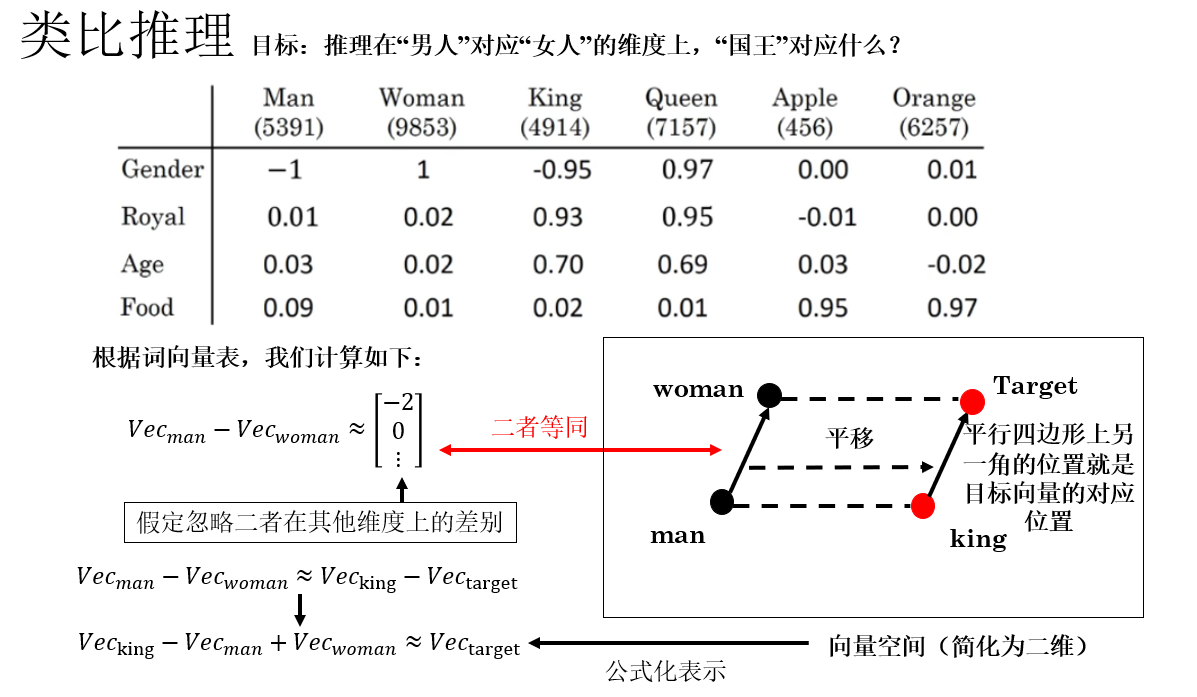
因此,你會發現,這部分計算:
實際上,是讓‘國王’沿着‘男人→女人’的語義方向平移,以此來得到一個目標向量,如果詞嵌入合理,那麼這個向量就會指向語義上最接近“王后”的位置。
到這裏,我們就得到了在男人對應女人的維度上,國王所對應的目標向量。
但是到這裏還沒有結束,我們還差一步,那就是找到在語義上距離目標向量最近的詞向量,得到類比結果。
因此,我們下一步的工作就是將目標向量與詞表中所有詞向量逐個計算相似度,再選取相似度最高的詞作為預測結果。
如何計算相似度?你可能會想到我們常用的歐氏距離。
然而,在詞嵌入空間中,直接使用歐氏距離並不是一個理想的選擇。
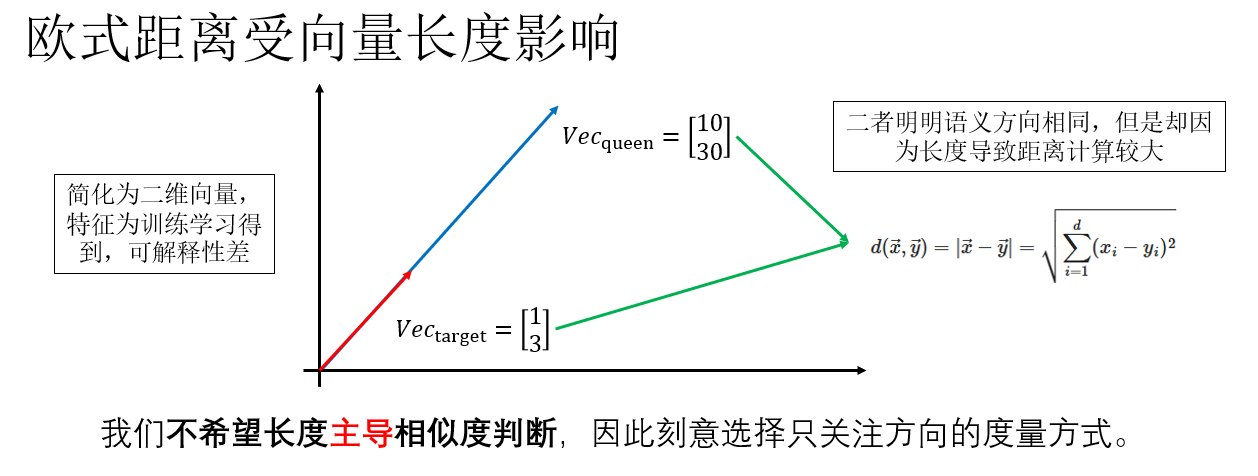
這是因為歐氏距離同時受到向量方向和向量長度的影響,雖然詞向量維度相同,但訓練目標並不會約束不同詞向量的長度一致。由於詞頻、梯度更新次數和優化路徑的差異,不同詞向量的範數往往不同,而這些長度差異並不一定對應語義差異。
聽起來很複雜,來舉個例子看看:
換句話説,在語義上非常接近的兩個詞向量,可能只是因為長度不同,在歐氏距離下被判定為“相距較遠”,從而干擾類比推理的結果。
相比之下,我們更關心的是: 目標向量與某個詞向量在語義方向上是否一致。
這正是餘弦相似度(Cosine Similarity) 所度量的內容。
餘弦相似度通過計算兩個向量夾角的餘弦值,來衡量它們在方向上的一致程度,其定義為:
其定義為:
其中,\(\vec{x} \cdot \vec{y}\) 表示向量的點積,\(|\vec{x}|\) 與 \(|\vec{y}|\) 分別表示向量的歐幾里得範數(向量各維度平方和的開方)。
可以看到,餘弦相似度在計算過程中對向量進行了長度歸一化,因此最終的結果只與兩個向量之間的夾角有關,而與它們的絕對長度無關。
從幾何角度來看,餘弦相似度實際上回答的是這樣一個問題: “這兩個向量指向的方向有多一致?”
當兩個向量方向完全一致時,夾角 \(\theta = 0^\circ\),此時 \(\cos(\theta)=1\)。
當兩個向量正交時,\(\theta = 90^\circ\),\(\cos(\theta)=0\)。
而當兩個向量方向相反時,\(\theta = 180^\circ\),\(\cos(\theta)=-1\)。
這與我們在詞嵌入中的直覺是高度一致的: 如果兩個詞在語義空間中表達的是相似或相關的含義,那麼它們的向量應當指向相近的方向,而語義無關的詞,其向量方向往往接近正交。
我們仍然用前面的例子再來演示一下:
顯然,這兩個向量方向完全一致,僅長度不同。
計算它們的餘弦相似度:
可以看到,儘管兩個向量在歐氏距離下“相距很遠”,但在餘弦相似度的度量下,它們被正確地判定為語義方向完全一致。
因此,在詞嵌入的類比推理任務中,我們通常採用餘弦相似度來衡量目標向量與詞表中各個詞向量之間的接近程度,從而選取語義上最合理的預測結果。
我們會在之後的詞嵌入模型中再展開為什麼有些詞向量的長度很大,而長度又代表了什麼。
由此,我們完成了使用詞嵌入來進行類比推理的過程,這不僅是詞嵌入的一項應用,我們也可以用它來檢驗詞嵌入模型對語義的理解能力。
3. 總結
| 概念 | 原理 | 比喻 |
|---|---|---|
| 詞彙表徵 | 將詞彙表示為多維連續向量(詞向量/embedding),以便模型計算和比較。 | 詞彙像嵌入在高維空間裏的點,距離反映語義相似性。 |
| 獨熱編碼(One-hot) | 每個詞用高維稀疏向量表示,向量間互相正交。 | 每個詞孤立存在,蘋果和橘子、男人和女人沒有聯繫。 |
| 詞嵌入(Embedding) | 將詞向量映射到同一向量空間進行學習和比較,低維、連續、可度量相似性。 | 像把高維詞彙空間“壓縮”成一個連續空間,詞語間距離反映語義。 |
| 類比推理 | 通過向量運算髮現詞彙間語義關係,公式:\(\vec{king}-\vec{man}+\vec{woman}\approx \vec{queen}\) | 國王沿“男人→女人”的語義方向平移,指向王后。 |
| 相似度計算 | 歐氏距離受向量長度影響,可能誤判語義;餘弦相似度只看向量方向 | 方向一致的向量被判定語義相近,即使長度不同。 |
| 餘弦相似度 | $$\cos(\theta) = \frac{\vec{x} \cdot \vec{y}}{|\vec{x}| , |\vec{y}|}$$ | 兩個向量方向一致就像箭頭指向相同方向,即使箭頭長短不同也一樣。 |
| 向量長度 | 主要受詞頻、梯度累計等訓練因素影響,不直接對應語義。 | 長度大不代表更“重要”,方向才決定語義關係。 |
| 可視化(t-SNE) | 將高維詞向量映射到2D/3D平面,儘量保留局部相似關係。 | 像把高維空間“攤平”,方便觀察詞語間距離。 |