此分類用於記錄吳恩達深度學習課程的學習筆記。
課程相關信息鏈接如下:
- 原課程視頻鏈接:[雙語字幕]吳恩達深度學習deeplearning.ai
- github課程資料,含課件與筆記:吳恩達深度學習教學資料
- 課程配套練習(中英)與答案:吳恩達深度學習課後習題與答案
本篇為第五課第三週的內容,3.2到3.5的內容。
本週為第五課的第三週內容,與 CV 相對應的,這一課所有內容的中心只有一個:自然語言處理(Natural Language Processing,NLP)。
應用在深度學習裏,它是專門用來進行文本與序列信息建模的模型和技術,本質上是在全連接網絡與統計語言模型基礎上的一次“結構化特化”,也是人工智能中最貼近人類思維表達方式的重要研究方向之一。
這一整節課同樣涉及大量需要反覆消化的內容,橫跨機器學習、概率統計、線性代數以及語言學直覺。
語言不像圖像那樣“直觀可見”,更多是抽象符號與上下文關係的組合,因此理解門檻反而更高。
因此,我同樣會儘量補足必要的背景知識,儘可能用比喻和實例降低理解難度。
本週的內容關於序列模型和注意力機制,這裏的序列模型其實是指多對多非等長模型,這類模型往往更加複雜,其應用領域也更加貼近工業和實際,自然也會衍生相關的模型和技術。而注意力機制則讓模型在長序列中學會主動分配信息權重,而不是被動地一路傳遞。二者結合,為 Transformer 等現代架構奠定了基礎。
本篇的內容關於束搜索,是在 seq2seq 模型中用於推理階段的解碼策略。
1. 序列生成的實質:條件概率
在開始束搜索之前,一個關鍵問題是: seq2seq 模型在“生成序列”時,本質上到底在做什麼?
答案是:序列生成,本質上是在建模並求解一個條件概率最大化問題。
這是整個模型邏輯的核心,我們來具體展開:
1.1 模型輸出:條件概率最大的序列
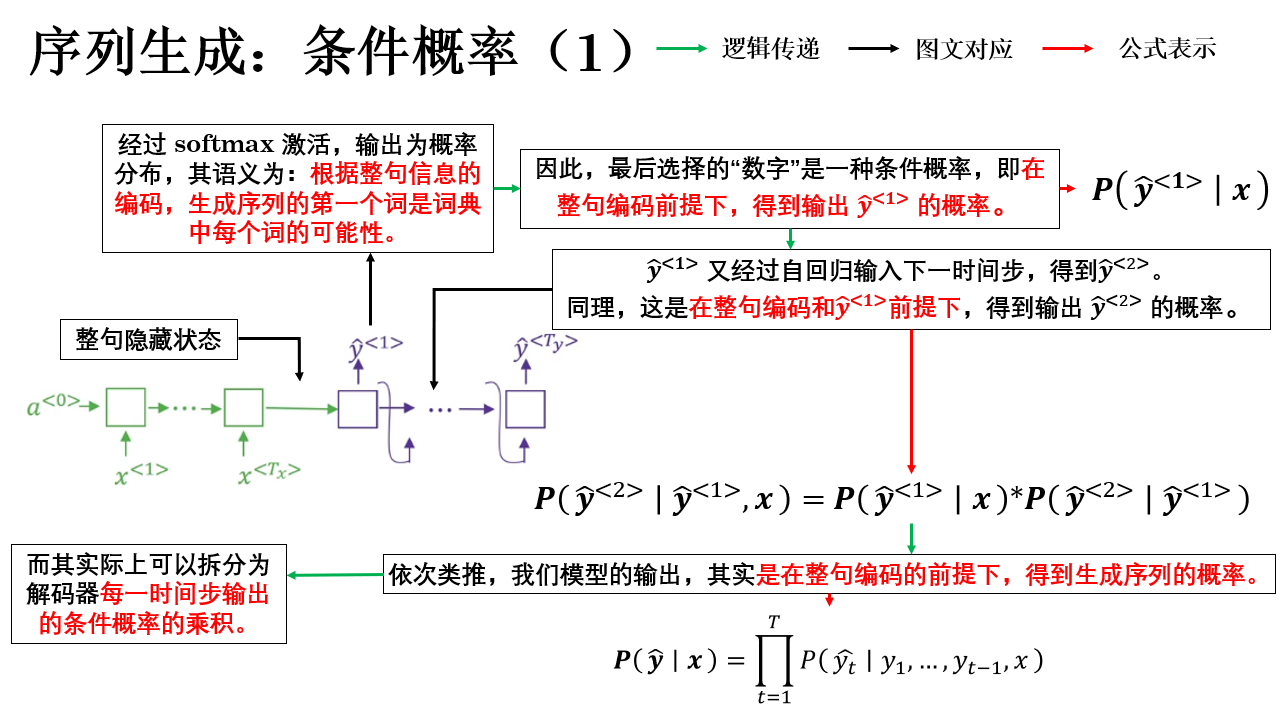
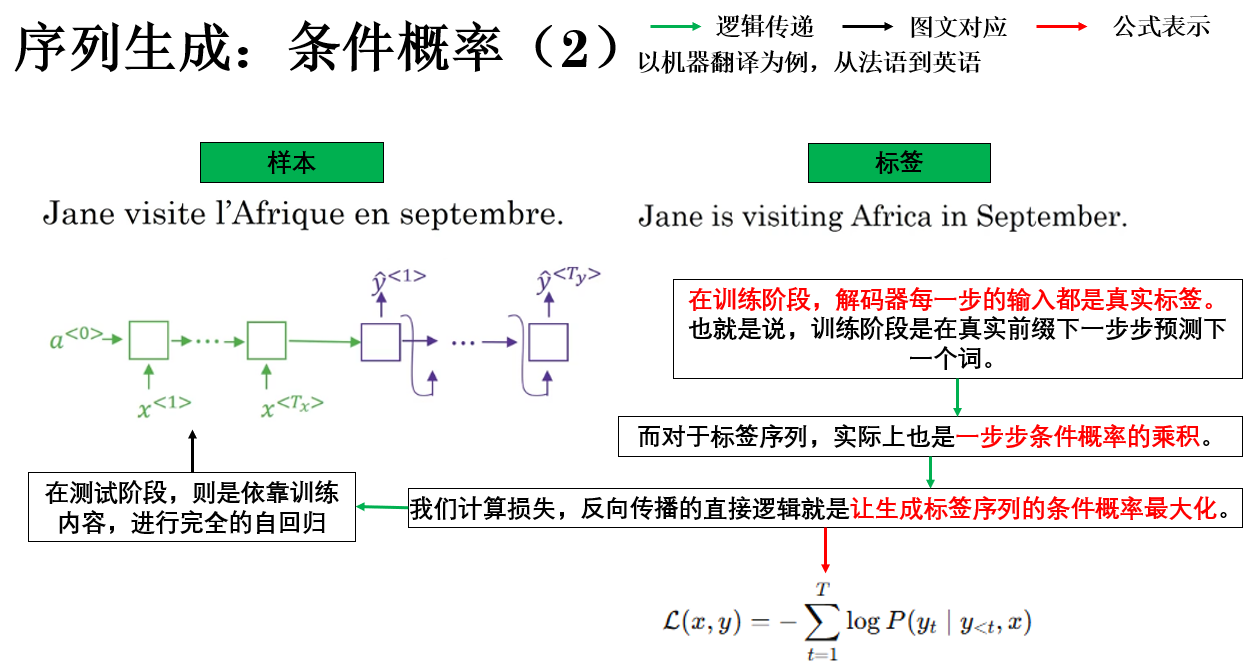
總結來説,seq2seq 模型真正面對的問題,是在所有可能的輸出序列中,找到一個條件概率最大的序列。
通過概率鏈式法則,整句的條件概率可以被分解為若干個逐時間步的條件概率的乘積。
因此,我們在訓練階段學習得到更真實的概率分佈,而在推理階段,輸出問題被轉化為一個搜索問題:需要在由詞表構成的序列空間中,尋找條件概率最大的那條生成路徑。
就像這樣:

但是,一個很明顯的問題出現了,如果把所有可能的生成路徑畫成一棵樹:深度為序列長度 \(T\)、每一層的分支數約為 \(|V|\),那麼完整搜索空間的規模大致為:\(|V|^T\)。
這是一個指數級增長的空間,顯然不可能被窮舉。
因此,你會發現,到這裏,問題居然迴歸到了搜索算法中。
1.2 最直接的搜索策略:貪心算法
我們知道,既然每一步都會生成對應的概率分佈,那麼一個最直接的策略就是:在每一個時間步都選擇條件概率最大的詞作為當前輸出,只保留這一條唯一的生成路徑。
這種做法通常被稱為貪心解碼(Greedy Decoding)。
從形式上看,貪心算法在第 \(t\) 步執行的是:
並將該結果立即作為下一步的輸入,直到生成終止符 EOS 或達到最大長度。
顯然,貪心算法最大的優勢在於極低的計算成本,它每一步只保留一個候選,不需要維護多條路徑。因此解碼速度快、內存佔用小,對同一輸入始終生成唯一輸出,結果穩定。
但是,貪心算法的缺陷也是老生常談了:局部最優不等於全局最優。
繼續用剛剛的例子:
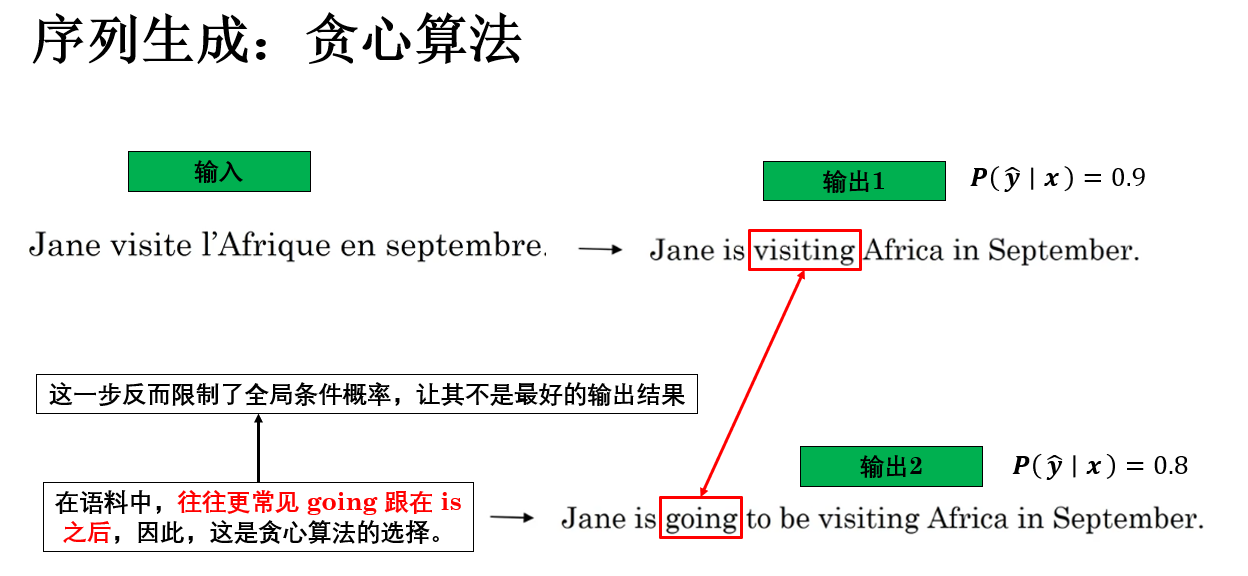
因此,由於貪心算法在每一步只關注當前條件下概率最大的詞,而完全不考慮未來的影響,很容易出現某一步看起來是“最合理”的選擇,但實際卻會在後續步驟中限制模型的表達空間,最終導致整條序列的聯合概率反而更低的情況。
總結來説,在對實時性要求較高、或對生成質量要求不高的場景中,貪心算法往往是一個工程上可接受的基線方案。但顯然,它並不是一個很好的選擇。
也正因為如此,我們才需要一種在計算代價可控的前提下,同時保留多條高概率候選路徑的搜索策略—— 這正是束搜索(Beam Search)要解決的問題。
2. 束搜索(Beam Search)
在理解了序列生成和貪心解碼後,束搜索的理解反而可以説是水到渠成,用一句話來概括束搜索:沒有那麼貪心的貪心算法。
貪心算法的問題在於,它只保留一條路徑,導致容易錯過整體概率更高的序列。
而束搜索的核心思想很簡單:
在每一步生成時,不只保留一個最優詞,而是保留前 \(k\) 條最有希望的候選序列,逐步擴展,最後從這些候選中選擇聯合概率最大的序列。
這裏的 \(k\) 就是我們稱為 束寬(beam width),它控制搜索的“寬度”:
- \(k=1\) 時,束搜索退化為貪心算法。
- \(k\) 越大,搜索空間越廣,生成結果越接近全局最優。
- \(k\) 太大,又會帶來計算開銷增加。
不難理解,下面具體展開一下:
2.1 束搜索的步驟
假設詞表大小為 \(|V|\),beam width 為 \(k\),束搜索的詳細步驟如下:
- 初始:從起始符
<BOS>開始,生成第一步所有詞的概率分佈,選取前 \(k\) 個概率最高的詞,組成初始候選序列。 - 擴展:對每條候選序列,生成下一步的所有詞的概率,計算每條擴展後序列的聯合概率。
- 保留:從 \(k \times |V|\) 條擴展序列中,選取聯合概率前 \(k\) 的序列作為下一步候選。
- 循環:重複步驟 2-3,直到每條候選序列生成 EOS 或達到最大長度。
- 輸出:從最終候選序列中選擇聯合概率最大的作為最終生成結果。
假設詞表 \(V = {A, B, C}\)、目標序列最大長度 \(T = 3\)、束寬 \(k = 2\),我們舉例來演示一下:
步驟 1:初始化
- 從起始符
<BOS>出發,生成第一步所有詞概率:$A=0.5, B=0.3, C=0.2 - 選前 \(k=2\) 個詞:A (0.5) 和 B (0.3)
此時的候選序列池:\([A], [B]\)
步驟 2:擴展第一步候選
假定下一步生成概率分佈如下:
| 候選序列 | A | B | C |
|---|---|---|---|
<BOS>+A |
0.1 | 0.6 | 0.3 |
<BOS>+B |
0.4 | 0.4 | 0.2 |
擴展過程為:
| 前一步序列 | 擴展詞 | 新序列 | 計算過程 | 聯合概率 |
|---|---|---|---|---|
[A] |
A | [A,A] |
0.5 × 0.1 | 0.05 |
[A] |
B | [A,B] |
0.5 × 0.6 | 0.30 |
[A] |
C | [A,C] |
0.5 × 0.3 | 0.15 |
[B] |
A | [B,A] |
0.3 × 0.4 | 0.12 |
[B] |
B | [B,B] |
0.3 × 0.4 | 0.12 |
[B] |
C | [B,C] |
0.3 × 0.2 | 0.06 |
此時的候選序列池:[A,B], [A,C]
步驟 3:擴展第二步候選
繼續,假設模型在第 3 步生成概率如下:
| 序列 | A | B | C |
|---|---|---|---|
[A,B] |
0.2 | 0.5 | 0.3 |
[A,C] |
0.6 | 0.1 | 0.3 |
同理:
| 前一步序列 | 擴展詞 | 新序列 | 計算過程 | 聯合概率 |
|---|---|---|---|---|
[A,B] |
A | [A,B,A] |
0.3 × 0.2 | 0.06 |
[A,B] |
B | [A,B,B] |
0.3 × 0.5 | 0.15 |
[A,B] |
C | [A,B,C] |
0.3 × 0.3 | 0.09 |
[A,C] |
A | [A,C,A] |
0.15 × 0.6 | 0.09 |
[A,C] |
B | [A,C,B] |
0.15 × 0.1 | 0.015 |
[A,C] |
C | [A,C,C] |
0.15 × 0.3 | 0.045 |
需要強調的是:遇到相同概率的序列,本質上束搜索並沒有硬性規定選哪條,可以根據場景選擇:先到先得、隨機或增加規則來提升多樣性。
最終,我們完成擴展如下:
| 排名 | 序列 | 聯合概率 |
|---|---|---|
| 1 | [A,B,B] |
0.15 |
| 2 | [A,B,C] |
0.09 |
因此最終輸出序列為:[A,B,B]
這就是束搜索的直觀機制:在可控開銷下,同時考慮多條路徑,提高生成序列的整體概率。
2.2 長度歸一化(Length Normalization)
在上面的例子中,我們看到束搜索通過聯合概率選擇了 [A,B,B] 作為最終輸出。
但是,在實際應用中,有一個容易被忽視的問題:聯合概率是每一步條件概率的乘積,序列越長,乘積值往往越小。
也就是説,如果我們直接用聯合概率來比較不同長度的序列,束搜索可能偏向生成短序列,因為它們乘起來的概率更大,而不是因為內容更合理。
因此,我們引入長度歸一化,它和 BELU 裏的長度懲罰有相同的出發點,但長度歸一化是在“生成階段做內部優化”,BLEU 長度懲罰是在“評價階段修正指標”,兩者原理類似,但作用環節不同。
具體來説,假設有兩條候選序列:
| 序列 | 聯合概率 |
|---|---|
[A,B,B] |
0.15 |
[A,B,B,C] |
0.14 |
其中,[A,B,B,C] 實際上可能更合理、語義更完整,但是因為聯合概率 0.14 < 0.15,直接比較會被 [A,B,B] 優先選中,這就是“短序列偏好”問題。
而長度歸一化的思路很簡單:
用聯合概率開根號或除以長度的函數,平衡序列長度的影響,使得長序列不會因為乘積小而被不公平地排除。
常見做法的就是加權歸一化,對於長度 \(T\) :
其中,\(\alpha \in [0,1]\) 是超參數,用來控制長度懲罰強度,而使用 log 用來防止下溢。
還是用剛剛的例子:
| 序列 | 聯合概率 | log 聯合概率 |
|---|---|---|
[A,B,B] |
0.15 | \(\log 0.15 \approx -1.897\) |
[A,B,B,C] |
0.14 | \(\log 0.14 \approx -1.966\) |
假設 \(\alpha = 0.7\),計算兩條序列的歸一化得分:
[A,B,B],長度 \(T=3\):
[A,B,B,C],長度 \(T=4\):
歸一化後:
| 序列 | 原聯合概率 | 歸一化得分 |
|---|---|---|
[A,B,B] |
0.15 | -0.981 |
[A,B,B,C] |
0.14 | -0.745 |
現在,[A,B,B,C] 得分更高,此時束搜索就會選擇更合理、更完整的長序列。
這樣就解決了短序列偏好問題,同時保留概率信息。
2.3 束搜索的誤差分析
到此為止,你會發現序列生成任務的性能被分成了兩部分:模型對概率分佈的擬合能力和搜索算法的搜索能力。
因此,在調試時的一個關鍵點就在於正確分析誤差是來自模型還是搜索算法。
我們有這樣一個方法來確認這一點:
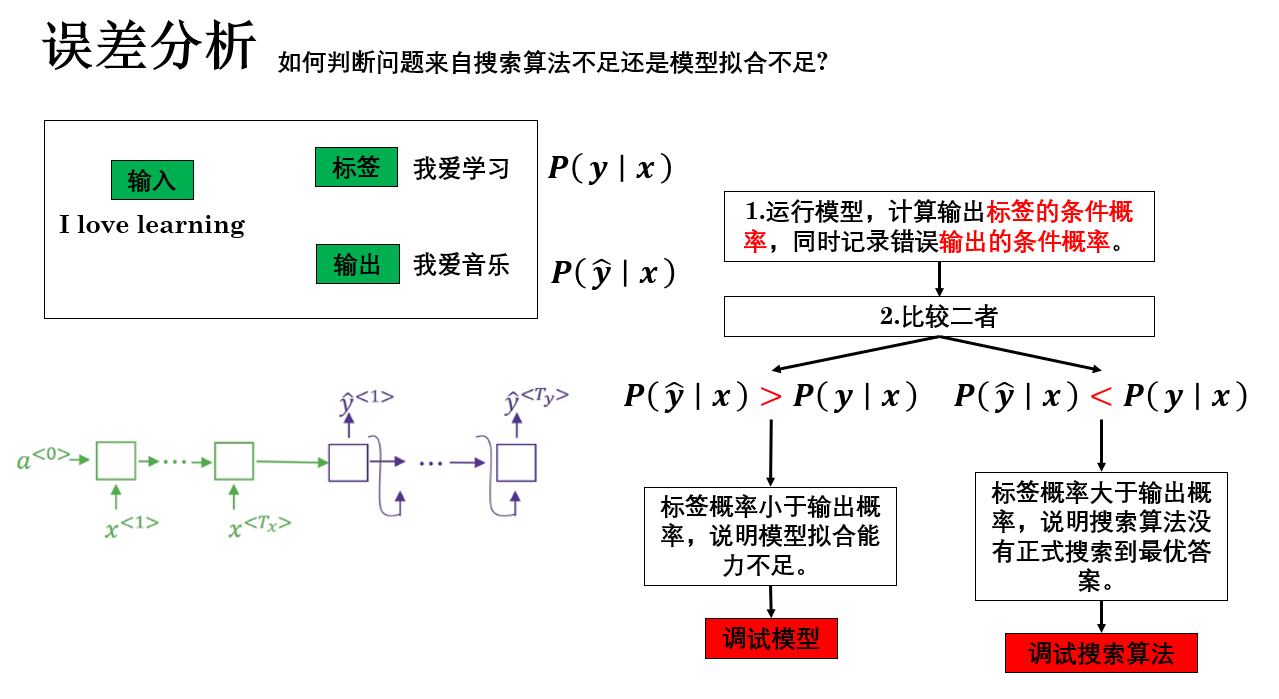
這樣,通過標籤序列的條件概率和輸出序列的條件概率的大小關係,我們就可以確認誤差來自模型還是搜索算法:
- 如果 \(P(\hat y|x) < P(y|x)\) → 搜索算法沒找到最優序列 → 調試搜索算法。
- 如果 \(P(\hat y|x) > P(y|x)\) → 模型預測概率不準 → 調試模型。
3. 總結
| 概念 | 原理 | 比喻 |
|---|---|---|
| 序列生成的本質 | seq2seq 模型在生成序列時,本質是求解條件概率最大的輸出序列,即 \(\mathbf{y}^* = \arg\max_\mathbf{y} P(\mathbf{y} \mid x)\),通過鏈式法則分解為逐步條件概率乘積。 | 找到所有可能路徑中“最順滑的一條”,像走迷宮選概率最高的路線。 |
| 貪心解碼 (Greedy Decoding) | 每一步選擇條件概率最大的詞作為輸出,只保留一條生成路徑,直到 EOS 或達到最大長度。 | 每次路口都選最寬的路,不管後面是不是死衚衕。 |
| 束搜索 (Beam Search) | 每一步保留前 \(k\) 條聯合概率最高的候選序列,逐步擴展,最後從候選中選聯合概率最大的序列。束寬 \(k\) 控制搜索空間大小。 | 沒那麼貪心的貪心算法,同時關注幾條有潛力的路線。 |
| 短序列偏好問題 | 聯合概率是條件概率乘積,序列越長乘積越小,束搜索可能偏向生成短序列。 | 短路優先:短的路線容易被選中,即便長的路線更合理。 |
| 長度歸一化 (Length Normalization) | 對聯合概率取 log 後除以序列長度的函數或加權冪,平衡長度影響,使長序列不會被排除。公式:\(\text{score}(\mathbf{y}) = \frac{1}{T^\alpha} \sum_{t=1}^{T} \log P(y_t \mid y_{<t}, x)\) | 給長路線加上“護欄”,讓它有機會被選中。 |
| 束搜索誤差分析 | 若 \(P(\hat y|x) < P(y|x)\) → 搜索沒找到最優序列,問題在搜索算法。
若 \(P(\hat y|x) > P(y|x)\) → 模型給了高概率錯誤序列,問題在模型預測。 |
最好的水果就在貨架上,但沒找到 → 找東西的方法有問題
拿到的水果比最好的水果看起來更好,但實際上不好吃 → 判斷水果質量的眼光不準 |

