此分類用於記錄吳恩達深度學習課程的學習筆記。
課程相關信息鏈接如下:
- 原課程視頻鏈接:[雙語字幕]吳恩達深度學習deeplearning.ai
- github課程資料,含課件與筆記:吳恩達深度學習教學資料
- 課程配套練習(中英)與答案:吳恩達深度學習課後習題與答案
本篇為第四課的第一週內容,1.9到1.11的內容,同時也是本週理論部分的最後一篇。
本週為第四課的第一週內容,這一課所有內容的中心只有一個:計算機視覺。應用在深度學習裏,就是專門用來進行圖學習的模型和技術,是在之前全連接基礎上的“特化”,也是相關專業裏的一個重要研究大類。
這一整節課都存在大量需要反覆理解的內容和機器學習、數學基礎。 因此我會盡可能的補足基礎,用比喻和實例來演示每個部分,從而幫助理解。
本篇的內容關於池化操作與卷積中的反向傳播,是對本週內容的最後補完,本篇之後,我們就可以對卷積神經網絡的基本組件與傳播過程有一個較完整的認知。
1. 池化層(pooling layer)
除去卷積層和全連接層,池化層也是卷積神經網絡的一大基石,不要被這個名字嚇到,它的原理反而是最簡單的。
常見的池化分為兩種:最大池化和平均池化。
使用方法並不難,我們直接擺出來:
- 最大池化:不計算,直接使用窗口最大值作為結果的卷積操作。
- 平均池化:用窗口所有像素的平均值作為結果的卷積操作。
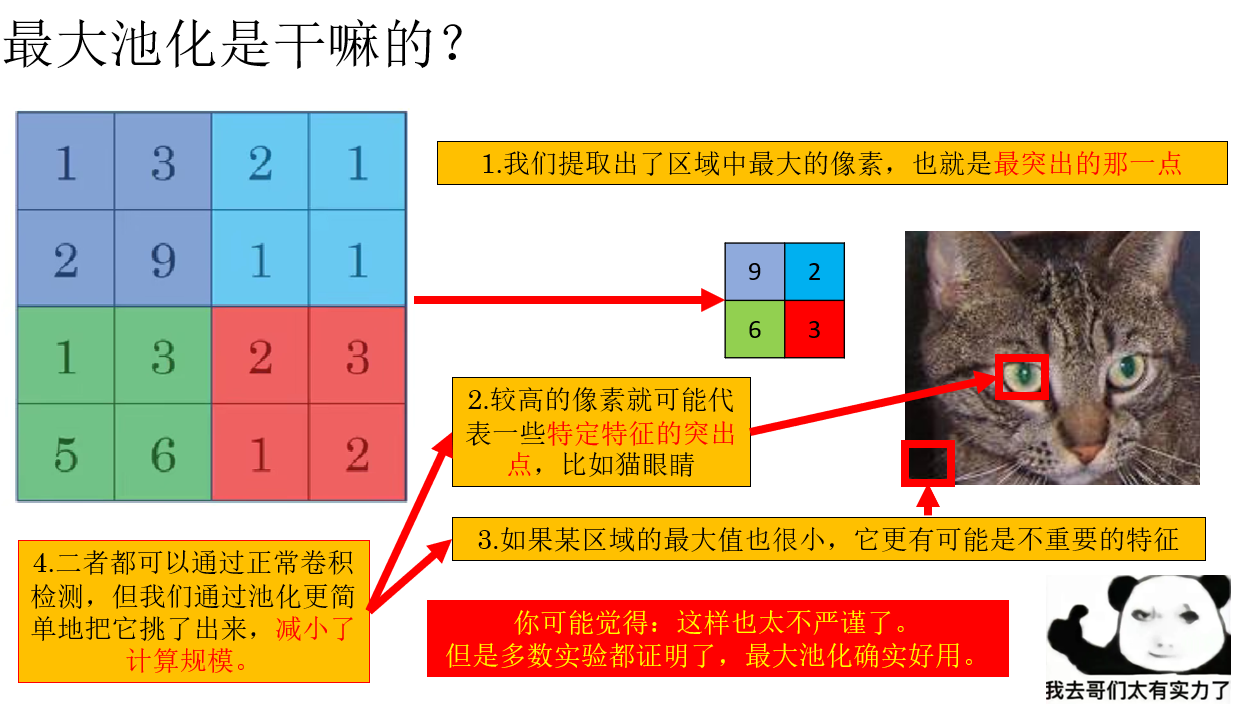
先來看最大池化,我們通過課程裏的例子補充一些細節:
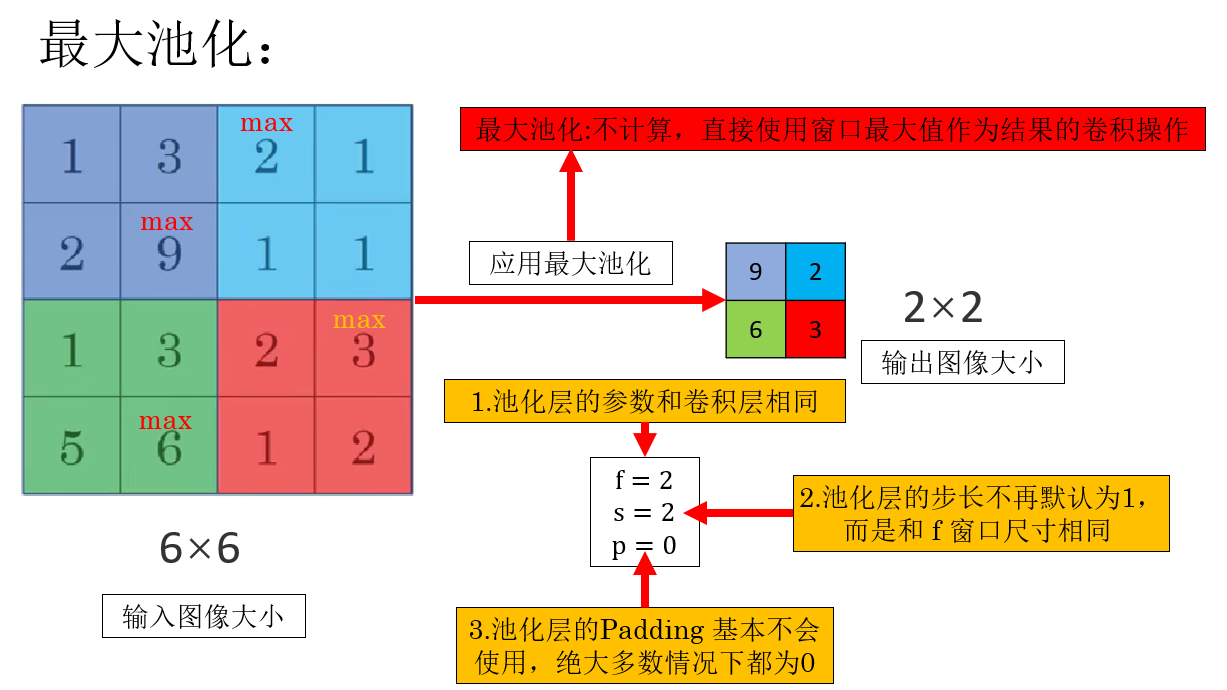
現在我們知道了最大池化怎麼用了,問題緊接着就來了,這個操作是用來幹嘛的? 我們繼續:
你可能發現了一個 bug :那萬一重要特徵反而是被一堆大像素包圍的小像素呢?這樣不是反而把最重要的特徵扔了嗎?
平均池化可以緩解這種現象:
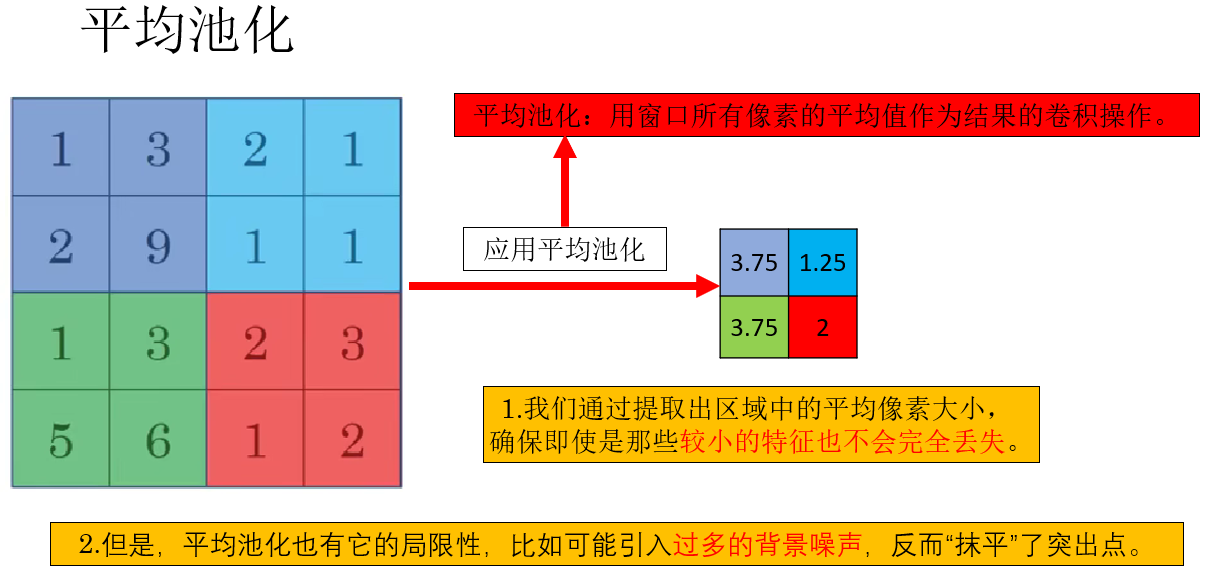
實際上,池化最大的作用就是在卷積神經網絡中減少特徵圖的空間尺寸來降低計算複雜度,同時保留特徵信息。
而對於怎麼池化更好更合適,還是要在具體任務中不斷嘗試。
此外,對於輸出特徵圖的大小計算,卷積的輸出公式在這裏仍然適用:
而對於多通道的池化處理,也和卷積核的邏輯相同,確保和輸入圖像的通道數相等。
最後強調一點:你會發現,池化層只有人工設置的超參數,沒有任何參與傳播的參數,在其之後通常也不單獨設置激活函數。
下面我們來看一個完整卷積神經網絡的傳播過程。
2. 卷積神經網絡的反向傳播
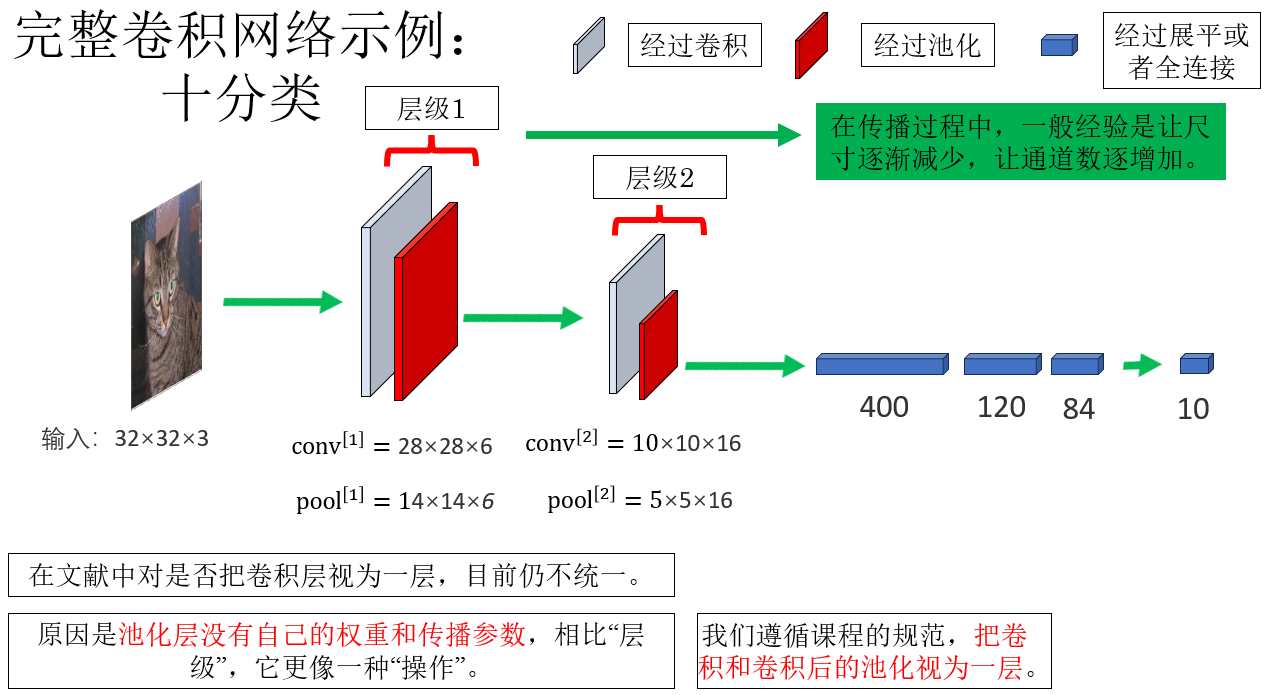
現在,我們先看一個加入了池化層的完整卷積網絡,補充一些細節:
另外一點要強調的是,和全連接網絡相通,就是儘量讓激活數(每次應用激活函數的元素數量)保持較平穩的下降趨勢。 避免出現”50000→1“這種斷崖式下降。
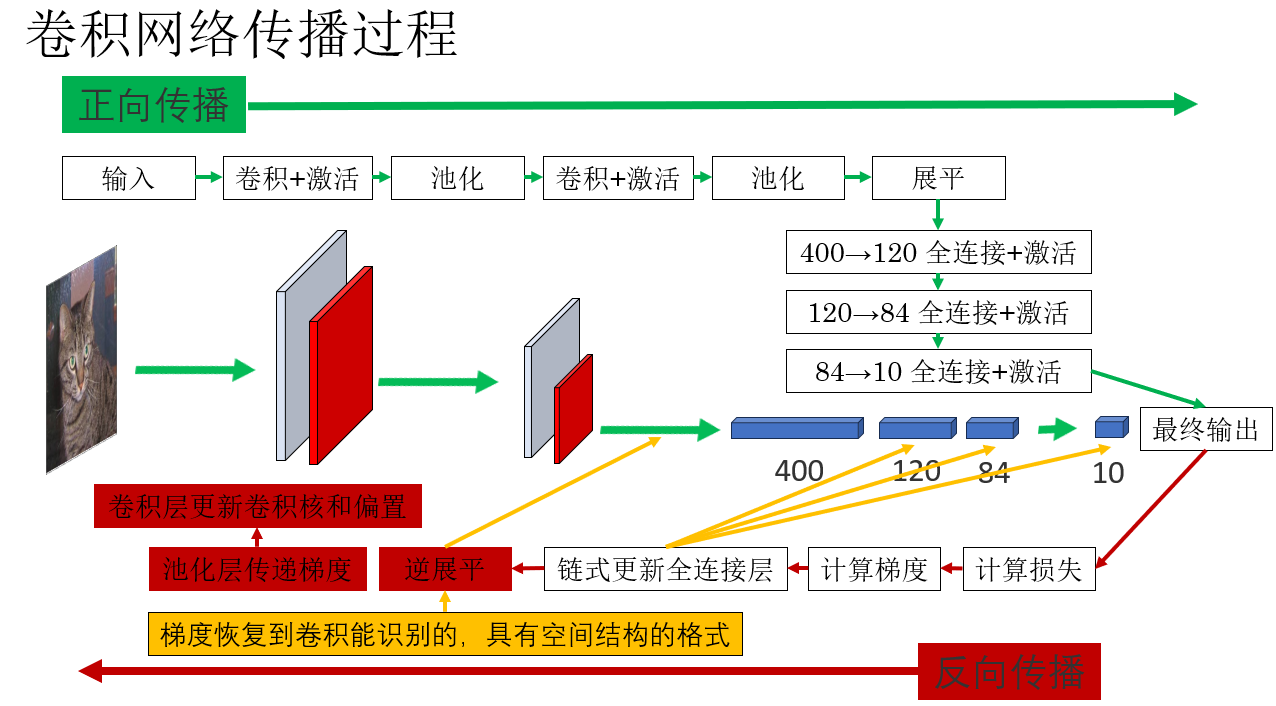
現在我們就來看看這個網絡的完整傳播過程。
很顯然,列舉出傳播過程後,問題緊接着就來了:當梯度到達卷積層的時候,我們是如何根據不確定數量的像素梯度更新確定數量的卷積核的呢?
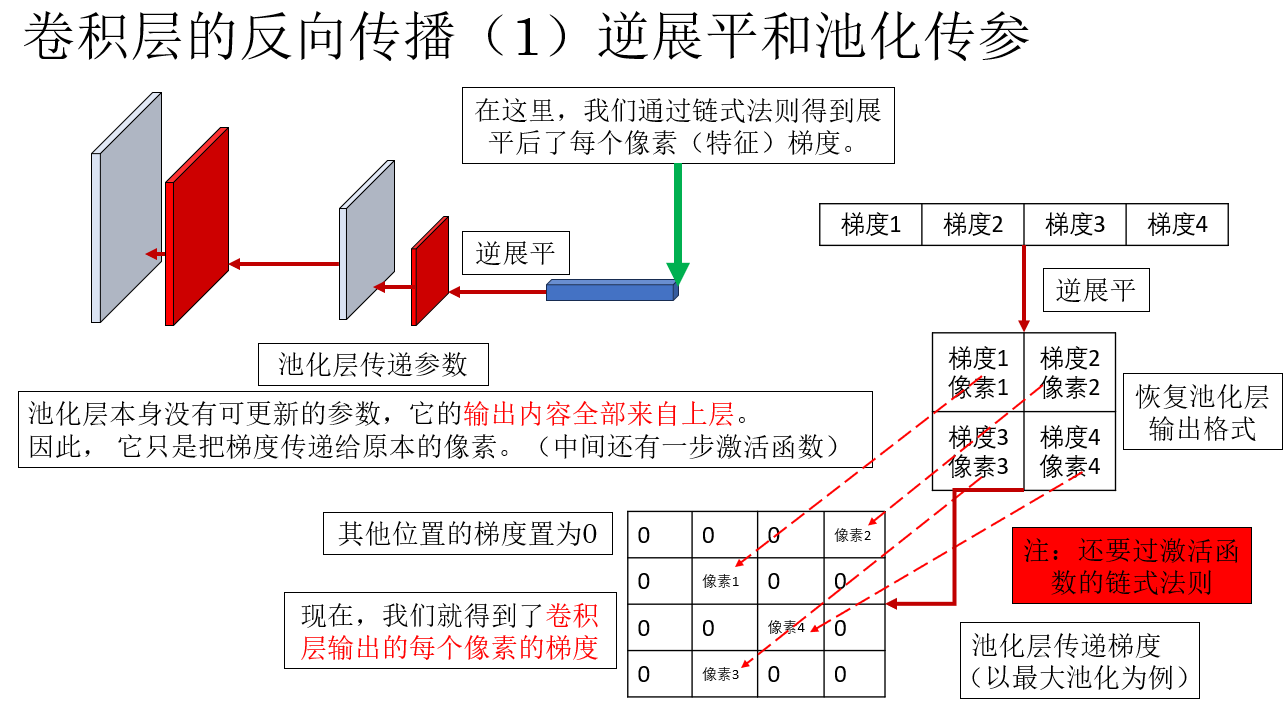
我們詳細展開一下標紅部分:
瞭解了逆展平和池化層傳遞參數後,就來到了最關鍵的部分:卷積核和偏置如何根據有空間結構的梯度更新? 繼續向下。
沒錯,因為輸出特徵圖中的每一個像素都是由卷積核與輸入圖像的區域運算後再加上偏置得到的,那麼就代表反向傳播計算得到輸出中每一個像素的梯度都和 9 個卷積核參數與 1個偏置常量相關。
知道了這個,如何更新就已經呼之欲出了:
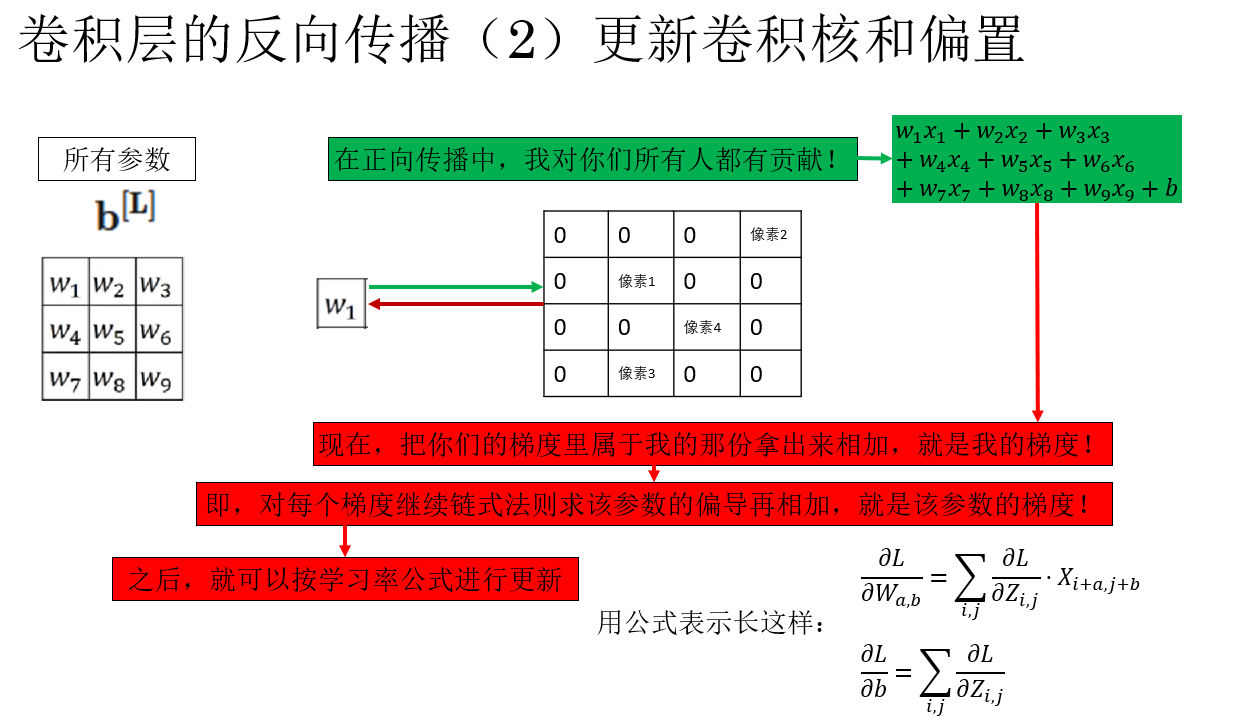
不寫複雜的公式,用一句話來概括就是:某個參數的最終梯度 = 它對所有受影響的輸出像素的偏導數之和。
如果你忘了偏導和梯度的概念,他們第一次出現在這裏:梯度下降法
這就是卷積層的反向傳播過程,繼續反向傳播也是同樣的道理。
最後,我們總結一下卷積層本身。
3.卷積層的特點
這一點的內容就更偏向理論了,相比全連接層,卷積層有兩個突出的特點,我們稱之為參數共享和稀疏連接。
來簡單介紹一下,不涉及太多具體應用,就不詳細展開了。
- 參數共享: 不同於全連接層對每個輸入特徵有單獨的權重,卷積層的輸入圖像共享卷積核和偏置參數。 原因是卷積核的適用性,我們可以用邊緣檢測卷積核檢測左上角的豎直邊緣,也可以用同樣的卷積核檢測右下角的豎直邊緣。
- 稀疏連接: 不同於全連接層的輸出和每個輸入都有關,卷積層輸出特徵圖中的每個像素只和產生他的幾個像素有關。 原因是圖像的局部性,要找貓耳朵,只要看耳朵那一塊就行了。
4. 總結
| 概念 | 原理 | 比喻 |
|---|---|---|
| 池化層(最大池化、平均池化) | 通過窗口取最大值或平均值,減少特徵圖空間尺寸,降低計算量,同時保留關鍵特徵;無參與訓練的參數。 | “把照片壓縮成縮略圖”:不用每個像素都看清,只保留輪廓和顯著信息。 |
| 池化層的尺寸計算 | 與卷積相同使用 \(\left\lfloor \frac{n - f + 2p}{s} \right\rfloor + 1\);通道數保持不變。 | “裁剪圖片”:窗口大小、步幅決定裁剪後的尺寸。 |
| 卷積層反向傳播 | 輸出每個像素的梯度都會對應卷積核全部參數;卷積核梯度是所有相關輸出像素偏導的總和;偏置梯度是所有輸出像素梯度的求和。 | “每個菜被客人打了幾分,後廚每個廚師要根據這些評分回溯自己哪一步影響了結果。” |
| 參數共享 | 同一個卷積核掃描整個圖像,因此所有位置使用同一組權重;大大減少參數量。 | “同一個模具印圖案”:不論紙放哪裏,模具都是同一個。 |
| 稀疏連接 | 卷積核只與局部區域相乘,一個輸出像素只依賴輸入的一小塊,而非整張圖。 | “你只需要看貓臉附近就能判斷有沒有耳朵,而不是看整張照片。” |