此分類用於記錄吳恩達深度學習課程的學習筆記。
課程相關信息鏈接如下:
- 原課程視頻鏈接:[雙語字幕]吳恩達深度學習deeplearning.ai
- github課程資料,含課件與筆記:吳恩達深度學習教學資料
- 課程配套練習(中英)與答案:吳恩達深度學習課後習題與答案
本篇為第四課的第三週內容,3.6到3.8的內容。
本週為第四課的第三週內容,這一課所有內容的中心只有一個:計算機視覺。應用在深度學習裏,就是專門用來進行圖學習的模型和技術,是在之前全連接基礎上的“特化”,也是相關專業裏的一個重要研究大類。
這一整節課都存在大量需要反覆理解的內容和機器學習、數學基礎。 因此我會盡可能的補足基礎,用比喻和實例來演示每個部分,從而幫助理解。
第三週的內容將從圖像分類進一步拓展到目標檢測(Object Detection) 這一更具挑戰性的計算機視覺任務。
與分類任務只需回答“圖中有什麼”不同,目標檢測需要同時解決“ 有什麼”以及“在什麼位置”兩個問題,因此在模型結構設計、訓練方式和評價標準上都更為複雜。
本篇的內容關於交併比、非極大值抑制和錨框,是對上一篇目標檢測算法對的一些補充。
1.交併比(Intersection over Union,IoU)
在分類任務中,我們介紹過一些評估指標來評估分類模型的性能,現在當任務從分類發展到檢測,自然也要有相應的評估指標來評估“定位的準不準”以及“有多準”。
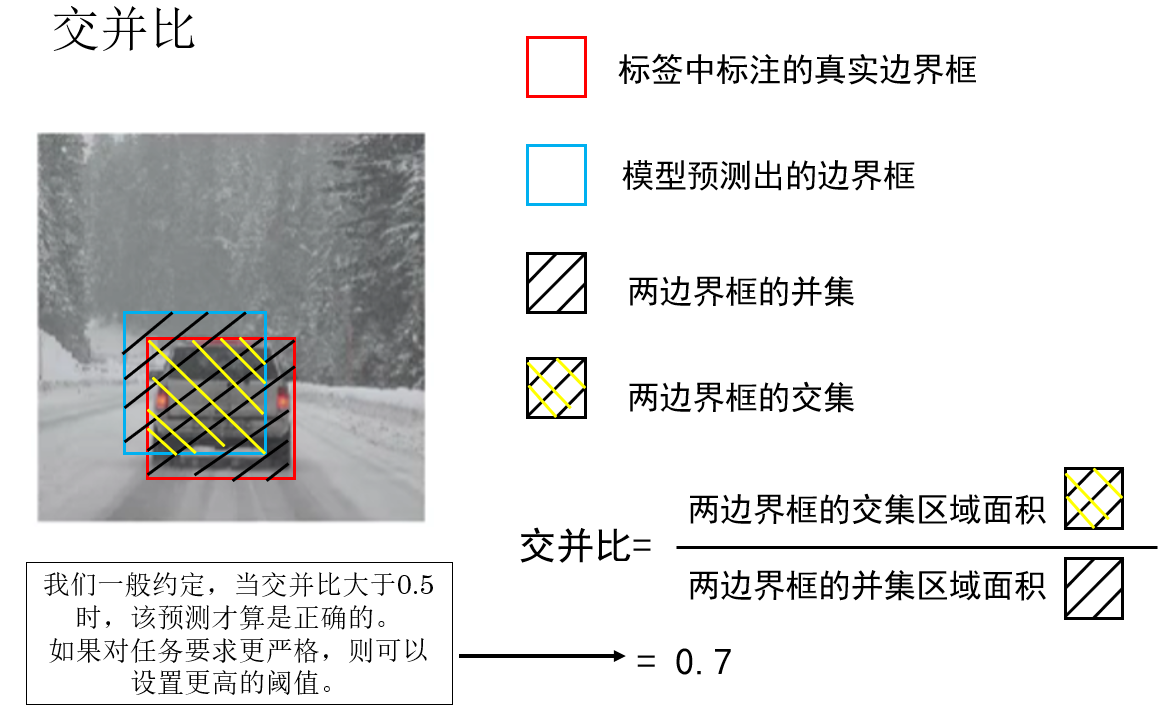
因此,交併比就是我們針對目標檢測任務而定義的評估指標,它的字面意思是“交集面積除以並集面積”,用於衡量兩個邊界框的重疊程度。
這個概念並不難理解,我們來看課程中裏例子:
很顯然,交併比越大,就代表我們預測的目標位置越接近真實值,模型的效果就越好:
- \(IoU = 0\):完全不重疊
- \(IoU = 1\):完全重合
並且,不同於之前我們使用的準確率,F1 分數等指標僅僅用作評估,我們還可以依靠交併比進一步提升模型性能。
怎麼做到?就是下面這一部分:
2. 非極大值抑制(Non-Maximum Suppression,NMS)
2.1 多個重疊預測框現象
在上一篇對 YOLO 算法的基礎介紹中,我們提到過,算法會將輸入圖像劃分為網格,每個網格獨立預測本網格內的目標,而我們在標註樣本的標籤時,會把目標歸入目標中心點所在網格中。
就像這樣:
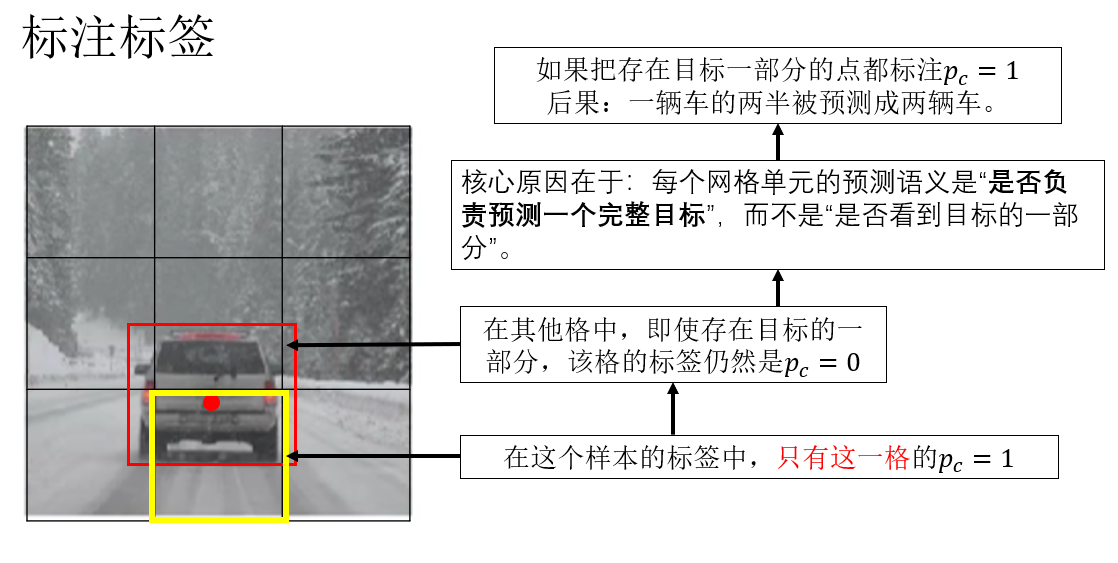
但是,這只是我們標註的邏輯。
在推理階段,模型並不知道“哪個網格被分配了哪個目標”,它只是在每個網格上獨立判斷“這裏是否存在目標”,並回歸一個可能的邊界框。
因此,當網格內存在目標特徵時,它就可能給出一個較高置信度的預測。
所以就會出現這樣一種現象:模型明明已經“找對了目標”,卻給出了很多個高度重疊的預測框。
就像這樣:
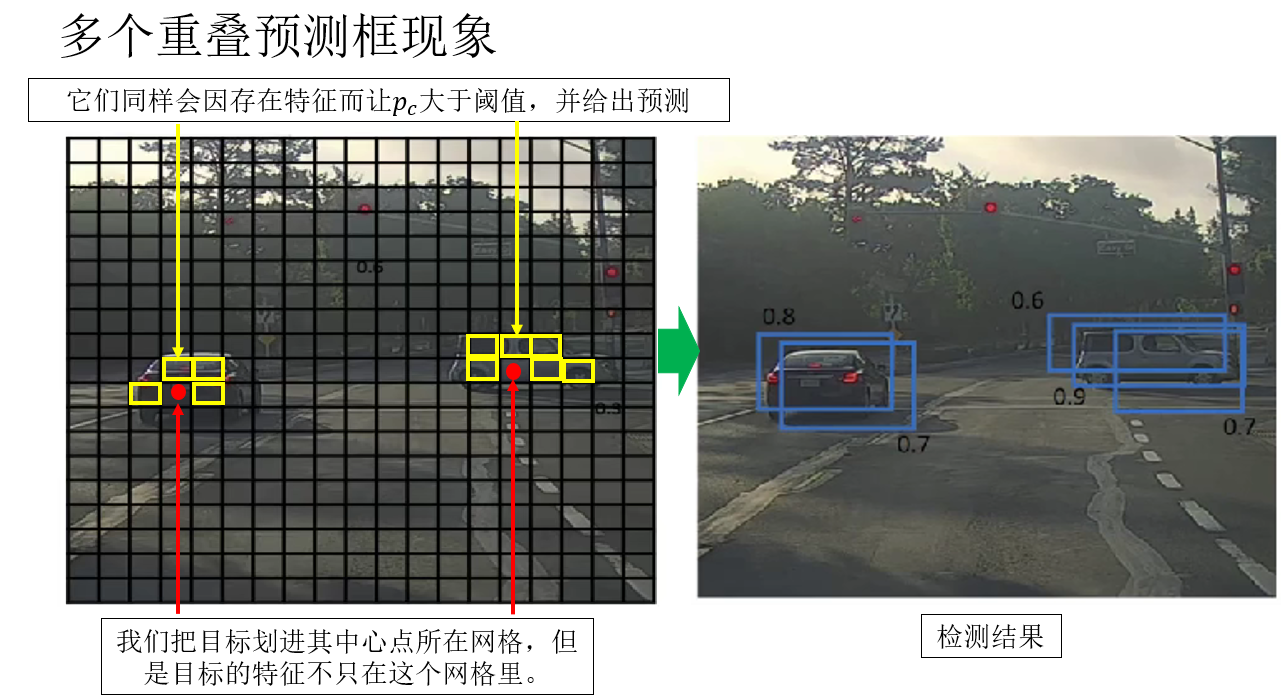
如果我們直接把這些結果全部輸出,會發生什麼?
答案是:一個目標被檢測成了很多個目標。
顯然,這並不是我們想要的結果。
所以,就有了非極大值抑制,來看看如何使用它。
2.2 應用非極大值抑制
非極大值抑制的作用,就是在這些高度重疊的“候選框”中,只保留最有代表性的那一個,其餘的全部抑制掉。
這裏的“高度重疊”,就是通過我們剛剛介紹的 IoU 來量化的。
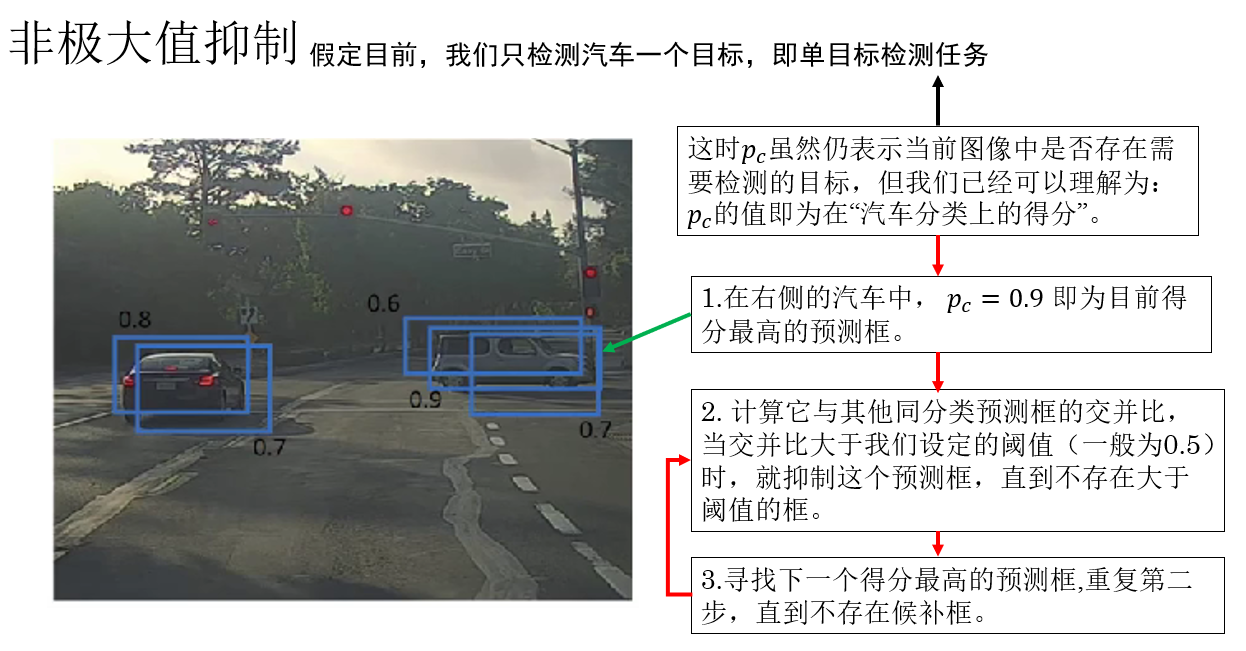
我們來看一下非極大值抑制的標準流程:
- 按置信度排序 :將所有預測框按照分類得分從高到低排序。
- 選出當前得分最高的框,作為最終結果之一 :這個框被認為是對某個目標的“最可信描述”。
- 計算該框與其他所有框的 IoU :如果某個框與當前框的 IoU 大於預設閾值(如 0.5),説明它們指向的是同一個目標。
- 抑制(刪除)這些高 IoU 的框 :只保留與當前框重疊程度較低的預測框。
- 重複上述過程,直到沒有候選框為止。
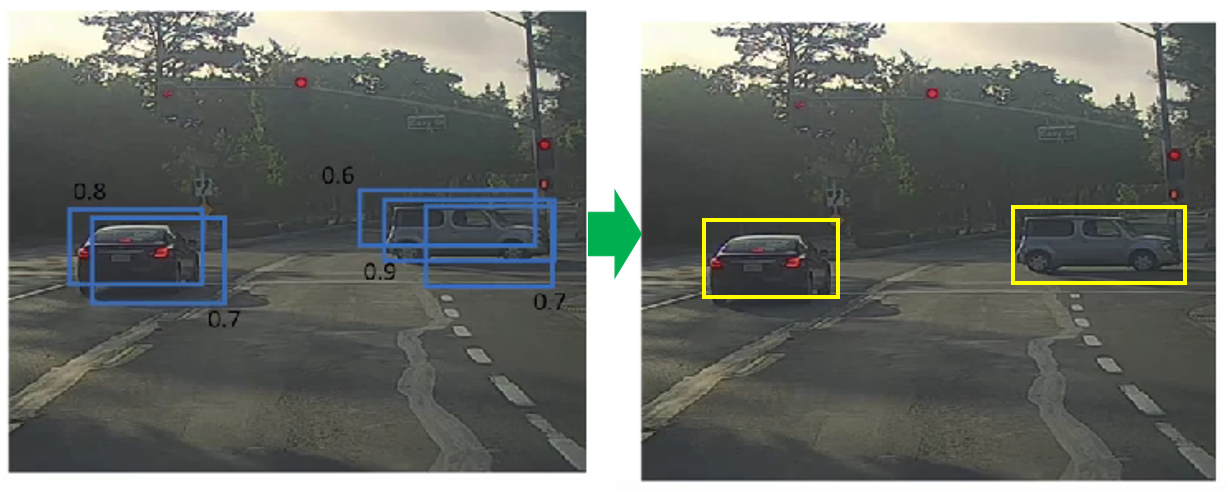
再演示一下,來看課程裏這個例子:
於是,應用非極大值抑制後,我們就得到了: 數量合理、位置準確、重複度極低的檢測結果。
2.3 預測框在傳播中的兩次篩選
在應用了非極大值抑制後,你就會發現,我們在對目標的預測過程中,為了得到更準確的結果,進行了兩次篩選。
(1)第一次篩選:基於置信度的“是否存在目標”
在模型完成正向傳播後,每一個網格都會給出一組預測,其中首先便是目標存在概率 \(p_c\)
這一步中,通常會先進行一次置信度閾值過濾:當 \(p_c\) 較低時,説明模型認為這裏更可能是背景,這些預測框會被直接丟棄。
只有 \(p_c\) 高於閾值的預測,才會進入下一階段。
這一步的作用是:快速過濾掉大量明顯的背景區域,減少後續計算量。
(2)第二次篩選:基於 IoU 的非極大值抑制
經過第一次篩選後,剩下的預測框已經基本都是:置信度較高且確實“命中目標特徵”的候選框
現在要解決的問題就是:它們可能仍然在描述同一個目標。
於是,就需要第二次篩選——非極大值抑制,即通過 IoU 進行比較,只保留最具代表性的預測框,其餘全部抑制掉。
這樣,我們最終才能得到一組:數量合理、位置準確、對應真實目標的檢測結果。
打個比方來理解:
第一次篩選是在問:“你確定你看到了東西嗎?”
第二次篩選是在問:“你們是不是都在看同一個東西?”
2.4 多個檢測目標:類別得分
我們現在已經知道了如何對單目標檢測任務進行非極大值抑制,可要是擴展到多分類呢?
這時,你會發現,我們不能再用 \(p_c\) 的大小來代表檢測目標的得分了。
因此,我們針對多目標檢測任務中選擇置信度最高的檢測框引入了一個新概念:類別得分。
它的公式並不難:
我們直接通過一個例子來説明它:
假設我們正在做一個 三分類目標檢測任務,需要檢測: 人(Person)、車(Car)、狗(Dog)
對於某一個預測框,模型給出瞭如下輸出:
表示: 該位置存在某個目標的置信度為 0.8。
同時,模型在“存在目標”的前提下,給出了類別預測概率:
在多類別目標檢測中,真正用於排序和篩選預測框的不是 \(p_c\),而是分類得分,代入上面的數值,我們得到:
- 人(Person): \(0.8 \times 0.1 = 0.08\)
- 車(Car): \(0.8 \times 0.7 = 0.56\)
- 狗(Dog): \(0.8 \times 0.2 = 0.16\)
該預測框最終會被判定為:“車”,它在“車”這一類別下的得分為:0.56
因此,在執行非極大值抑制時:該框會參與“車”類別的非極大值抑制,並與其他“車”類預測框按照 0.56 的得分進行排序和抑制。
總結一下:在多類別目標檢測中,\(p_c\) 只負責判斷“是否存在目標”,真正用於篩選、排序和執行 NMS 的,是結合了類別信息的“分類得分”。
3. 錨框(Anchor Boxes)
3.1 為什麼需要錨框?
在前面的內容中,我們默認了一個前提: 每個網格只預測一個邊界框。
這種設定在“目標數量較少、尺度差異不大”的場景下是可以工作的,但它很快就會暴露出一個致命問題: 一個網格里,可能同時存在多個不同目標。
如果同一個網格中:
- 既有一個高而瘦的人。
- 又有一輛矮而寬的車。
這時,如果我們仍然強制這個網格只預測一個邊界框,那麼顯然,很可能二者都無法被較好地定位。
這不是訓練不充分的問題, 而是面對多目標檢測,輸出空間本身不夠用。
錨框的引入,本質上就是為了解決多目標檢測中,同一網格中出現多個不同形態的目標而導致的定位混亂現象。
3.2 如何使用錨框?
錨框的思想可以用一句話概括:不再讓模型“從零開始”去猜邊界框,而是讓它在多個“預設形態”的參考框基礎上進行微調。
具體做法是:在每一個網格位置預先放置 \(K\) 個形狀不同的參考框,這些參考框就是錨框。
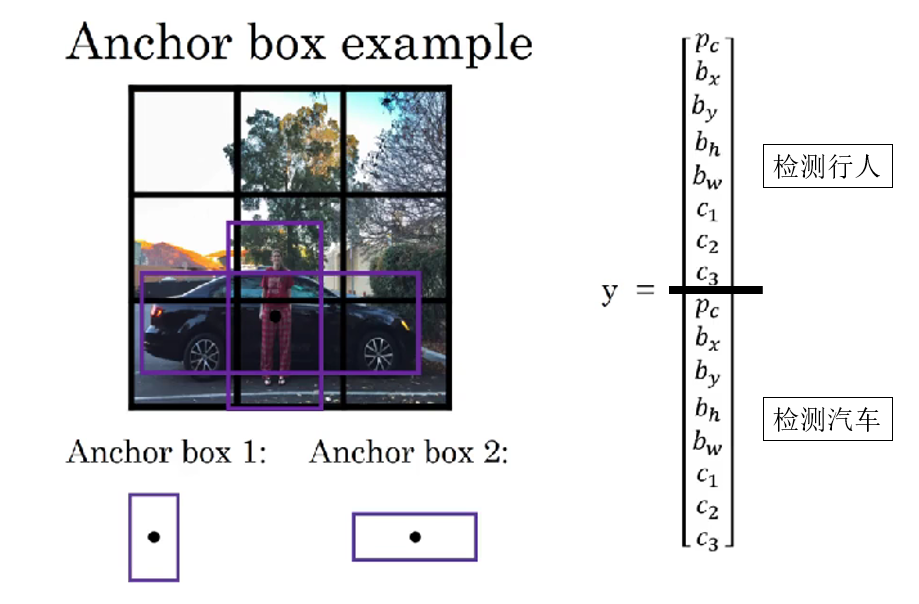
例如:我們預先知道預測目標一個是人,一個是汽車,於是便預先為每個網格設置兩個錨框:
- 一個偏高偏瘦,用來預測行人位置。
- 一個偏矮偏寬,用來預測汽車位置。
就像課程裏這樣:
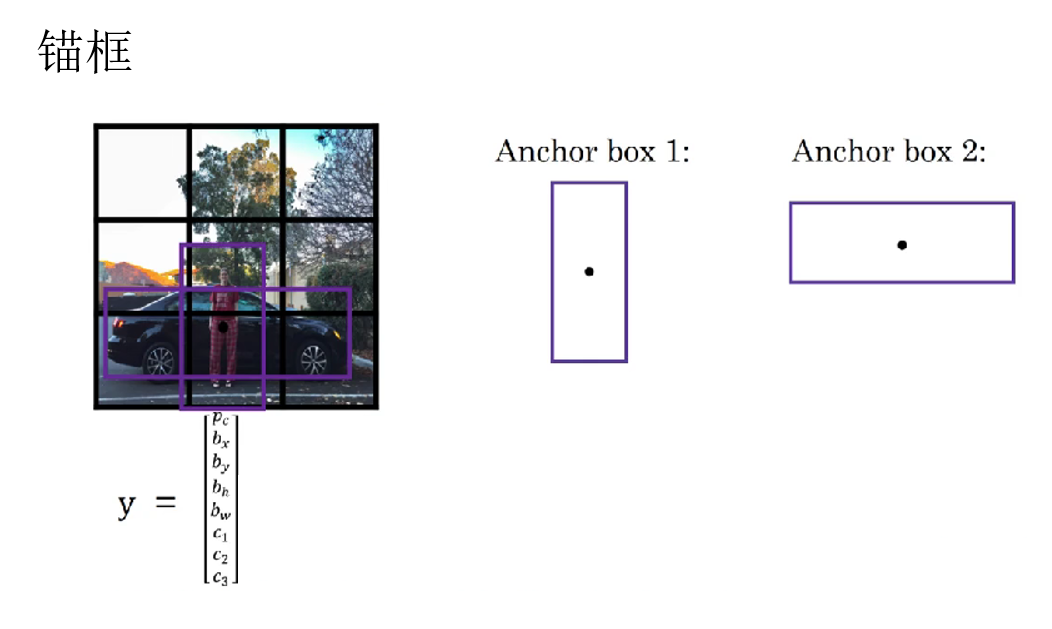
於是,一個網格不再只輸出一組預測,而是輸出 \(K\) 組預測結果,分別對應這 \(K\) 個錨框。
3.3 當同一個網格中可能出現多個目標時的標籤變化
我們知道,在之前,我們假定一個網格中只會出現一種目標,因此,我們這樣定義標籤:
但很顯然,當一個網格中可能出現多個目標時,一組標籤是不夠用的。如果網格里同時出現了行人和汽車,我們就要為它們各自設置一組標籤來讓網絡學習。
同理,當一個網格不再只輸出一組預測,而是輸出 \(K\) 組預測結果時,我們就要為其設置 \(K\) 組標籤:
就像這樣:
現在,我想你可能會有一個問題:我通過更改標籤適應了同一網格中存在多種目標的情況,那網絡不是就可以直接學每個目標的檢測了嗎?錨框是不是不設置也沒有問題?
別急,我們瞭解完錨框的具體使用邏輯,這個問題自然會迎刃而解。
3.4 標籤如何使用錨框
首先,在多錨框機制下,每個網格不僅有 \(K\) 個預測框,還對應 \(K\) 組標籤。這些標籤並不是隨意分配的,而是與錨框緊密對應,形成訓練的監督信號:
- 對於每個網格內的每個錨框,計算它與所有真實目標框的 IoU。
- 將 IoU 最大的目標分配給該錨框,該錨框就是正樣本錨框。
- 如果某個錨框與任何目標 IoU 都低於閾值,則該錨框為負樣本,其標籤 \(p_c=0\),其他參數忽略。
這樣,我們就完成了錨框和要檢測的目標的匹配。
同時,錨框機制還把位置信息的學習轉換為錨框中心和大小的微調。也就是説,網絡不再直接去預測目標在圖像中的絕對位置和尺寸,而是預測目標相對於錨框的偏移量和縮放比例。
它並不是改變標籤裏的位置信息的語義,而是通過運算將原本的絕對尺度轉換為相對錨框的偏移量並學習。
我們這裏不擺複雜的公式,瞭解原理即可。
這部分其實和殘差學習的邏輯有一定的相似之處:只需預測相對於參考框的微調量,降低了學習難度,使網絡更容易收斂並穩定檢測多目標。
現在,我們再來解釋上面的問題:
你會發現 : 錨框其實是我們人為幫助模型進行目標檢測的一種手工設計。
如果你只是簡單地在標籤中為同一網格增加多組目標信息,而不使用錨框,就會遇到這樣幾個問題:
- 沒有錨框的目標匹配,輸出與標籤會匹配混亂。
- 沒有錨框的偏移學習,面對多目標任務會收斂困難。
- 沒有錨框的“個性定製”,網絡多目標檢測的能力不足。
3.5 小結
這部分內容較多,我們簡單小結一下:
錨框的引入是為了解決單網格只能預測一個目標而無法處理同網格多目標的問題,通過在每個網格預設多個不同形狀的參考框,讓網絡只需預測目標相對於錨框的偏移量和類別概率,從而簡化學習任務並提高收斂性。
每個網格對應 \(K\) 個錨框,也就對應 \(K\) 組標籤,通過與真實目標的 IoU 匹配確定正負樣本。
如果沒有錨框,網絡在多目標檢測中容易出現目標匹配混亂、偏移量學習困難和收斂不穩定等問題。
錨框本質上是一種人為設計的參考機制,用來幫助網絡更高效、穩定地完成多目標檢測。
4. 總結
| 概念 | 原理 | 比喻 |
|---|---|---|
| 交併比(IoU) | 衡量預測框與真實框重疊程度,計算公式為交集面積除以並集面積,越大表示預測越準確 | 就像量尺量兩個重疊物體的重合面積,越大説明測量越精確 |
| 非極大值抑制(NMS) | 對候選預測框進行篩選,先按置信度排序,保留最可信預測框,再根據 IoU 刪除重疊度高的框 | 第一次篩選:問“你確定看到東西了嗎?”,第二次篩選:問“你們是不是都在看同一個東西?” |
| 置信度(\(p_c\)) | 預測該網格存在目標的概率 | 判斷“這裏有沒有東西” |
| 類別得分(Class Score) | 用 \(p_c \times c_n\) 表示某類別的最終得分,用於多類別 NMS 排序 | 確定目標的“身份得分”,選擇最可能的類別進行抑制 |
| 錨框(Anchor Boxes) | 在每個網格預設多個不同形狀的參考框,讓網絡只需預測相對於錨框的偏移量和類別概率,每個錨框與真實目標通過 IoU 匹配形成正負樣本 | 就像給網絡提供模板,讓它只需微調而不是從零猜測,類似殘差學習只學變化量 |
| 標籤變化 | 每個網格輸出 \(K\) 組預測,對應 \(K\) 組標籤,分別匹配不同錨框 | 原本一個網格只需寫一份作業,現在每個模板都寫一份作業 |
| 錨框作用 | 解決單網格多目標、提高收斂性、穩定訓練 | 給網絡參考框,讓它“照模板微調”而不是盲目猜測 |