此分類用於記錄吳恩達深度學習課程的學習筆記。
課程相關信息鏈接如下:
- 原課程視頻鏈接:[雙語字幕]吳恩達深度學習deeplearning.ai
- github課程資料,含課件與筆記:吳恩達深度學習教學資料
- 課程配套練習(中英)與答案:吳恩達深度學習課後習題與答案
本篇為第三課的第二週內容,2.8的內容。
本週為第三課的第二週內容,本週的內容關於在上週的基礎上繼續展開,並拓展介紹了幾種“學習方法”,可以簡單分為誤差分析和學習方法兩大部分。
其中,對於後者的的理解可能存在一些難度。同樣,我會更多地補充基礎知識和實例來幫助理解。
本篇的內容關於多任務學習,同樣是在模型學習方式上的一種拓展。
1. 多任務學習
在上一篇的遷移學習中,我們知道,把一個任務的模型遷移到另一個任務中應用的前提是:兩個任務的低層次特徵十分相似。
現在在這個點子的啓發下,又有人提出了新的想法:
既然多個任務的底層特徵十分相似,那能不能在一個網絡裏同時訓練針對這多個任務的模型?
這就是多任務學習的基本思想。
理解多任務學習,你可以把它想象成讓同一個大腦,同時學會幾件相互關聯的事情。
在深度學習中,就是用一個模型,同時去做多個任務,而不是每個任務都訓練一個獨立模型。
為什麼要這樣做? 原因就是上面提到的,因為一些任務之間其實共享着大量底層特徵。
舉個例子:
在這種共享基礎的前提下,單任務學習就像讓學生分別學習語文、歷史、寫作,但明明這些科目都依賴閲讀理解能力,結果你卻讓他重複學三遍閲讀方法,顯然不高效。
可能還是不太清楚,下面我們用課程裏一個非常典型的例子來説明:
1.1 自動駕駛系統的路面識別
假設你正在開發一個自動駕駛系統,它需要識別:
- 行人檢測
- 紅綠燈識別
- 路標識別
- 車輛檢測
現在,如果你為這些任務分別訓練 4 個模型,那麼它們都會學到:
- 圖像邊緣
- 物體輪廓
- 顏色分佈
- 基本幾何形狀
而這些“底層特徵”本質上是一樣的。
在這時,多任務學習的做法是:讓模型的前幾層共享,後面的部分再根據不同任務分頭進行。
繼續上面的學生上課的例子,多任務學習就像:
先讓學生統一上“基礎課”(數學、邏輯、閲讀),然後再按照專業分流各學科。
這樣做有三個顯著好處:
- 底層特徵共享,訓練更快
- 多個任務互相幫助,提高泛化能力
- 不用為每個任務單獨準備海量數據
尤其是當某些任務數據較少時,多任務學習往往能讓弱任務因為“借到其他任務的經驗”而表現更好。
瞭解了多任務學習的概念後,我們來看看它的適用範圍。
1.2 何時適合多任務學習?
多任務學習不是萬能的,它在以下條件下最有效:
- 多個任務之間具有相關性。
- 它們共享大量底層結構(如共同處理圖像、共同處理語音)。
- 數據量有限,希望通過共享知識彌補某個任務的不足。
此外,機器終究是由我們人設計的,因此,對於是否適用多任務學習,一個最符合直覺的判斷方式就是:如果一個人掌握任務 A 的知識後會更容易學會任務 B,那機器學習模型也可能如此。
例如:
- 識別貓的種類 + 判斷貓的姿勢
- OCR 文本識別 + 文本方向校正
- 情感分析 + 主題分類
- 車道檢測 + 路面分割
但如果任務之間差異很大,比如“人臉識別”和“花卉識別”,強行多任務反而會變成負擔,讓模型不知道優先學習什麼,最終效果反而變差。
現在,我們就來看看到底如何實現多任務學習。
1.3 多任務學習的實現邏輯
實際上,我們在多值預測與多分類那一節裏就簡單提到過這部分內容,現在才正式展開。
回憶一下最初的內容,在單任務學習中,我們的數據通常表示為一組樣本對:
其中
- \(x^{(i)}\) 是輸入樣本
- \(y^{(i)}\) 是樣本對應的“單個任務標籤”
但在自動駕駛系統中,一張路面圖片往往需要同時識別多個內容,這意味着對同一個輸入 \(x^{(i)}\),原本只有一個標籤,現在變成了多個標籤。
在開始前,再用我們的貓狗分類器舉例再理解一下這句話:
原本我們的數據集樣本中只會存在貓或者狗中的一種,相應的標籤自然就只有貓或狗。
現在任務改變,樣本中出現了貓和狗的“合照”,標籤自然也會增加,實現同時識別貓和狗的多任務學習。
舉完這個簡單的例子後,我們來正式展開這一部分。
(1) 多個任務的標籤如何組織?
繼續用前面的自動駕駛例子。現在一張圖像 \(x^{(i)}\),我們需要它同時給出:
- 有沒有行人(是/否)
- 有沒有車輛(是/否)
- 有沒有路標(是/否)
- 有沒有紅綠燈(是/否)
這裏先強調一下,我們只是使用這個語境來了解多任務學習,實際邏輯遠比這要複雜。
現在,單任務的標籤 \(y^{(i)}\) 就不夠用了,我們需要讓它變成一“組”標籤,就像這樣:
其中 :
- \(y^{(i)}_1\):行人檢測
- \(y^{(i)}_2\):車輛檢測
- \(y^{(i)}_3\):路標檢測
- \(y^{(i)}_4\):紅綠燈檢測
於是,從結構上看,\(y^{(i)}\) 就不再是一個標量,而是一個代表“任務集合”的向量。
來看一個實例:
假設現在有一張路口照片 \(x^{(i)}\),內容如下:
- 畫面中有行人。
- 畫面中也有車輛。
- 沒有看到任何路標。
- 畫面中有紅綠燈。
那麼,這張圖片的多任務標籤就是:
而如果讓任務再複雜一些,我們還會具體對紅綠燈進行三分類,於是又加入了獨熱編碼,例如:
在這種情況下,這張圖片的最終標籤就變成了:
總之,一個輸入 \(x^{(i)}\),多行標籤一起出現,這就是多任務學習在標籤維度上的直接體現。
説到這裏,你可能會有這樣一個問題,多任務學習與應用獨熱編碼的多分類都把標籤從標量變成了向量,這不會混淆嗎? 我們在這個問題上簡單展開一下。
(2)多標籤與應用獨熱編碼的多分類辨析:互斥性
在多任務學習中,經常會看到這樣的表達:
- 某些任務是“多標籤”
- 某些任務會用獨熱編碼
- 兩者都長得像一串 \((0,1)\) 組成的向量
就像剛剛的:
雖然它們看起來很像,但本質完全不同。
依舊以自動駕駛為例,你要判斷一張圖片裏:
- 有沒有人(是/否)
- 有沒有車(是/否)
- 有沒有路標(是/否)
- 有沒有紅綠燈(是/否)
這四件事之間互不影響。
畫面裏可以同時出現行人 + 車輛 + 紅綠燈,也可以一個都沒有。
因此,每個標籤都是一個獨立的二分類任務:
這裏的四個 \(y^{(i)}_k\) 都是“自由的”,可以同時為 1。
也就是説多任務學習的任務間沒有互斥性,sigmoid更適用這種邏輯。
現在再説説多分類:
紅綠燈狀態只有三種:紅、黃、綠 。
它們不能同時出現,因此需要用獨熱編碼:
這個編碼的特點是:存在互斥性,向量中只能出現一個 1,因此通常接 softmax 激活函數。
如果你有點忘了,它第一次出現在這裏:獨熱編碼
因此,這不是“多標籤”,而是“單標籤多分類”。
總結一下,區分二者的關鍵就是標籤間的互斥性,即是否允許多個標籤同時為 1。
能同時為 1 的就是“多標籤”,不能同時為 1 的就是“多分類(獨熱編碼)”。
(2) 多任務學習的模型結構長什麼樣?
我們先按照課程裏的內容,看一看最簡單的多任務學習模型長什麼樣子。
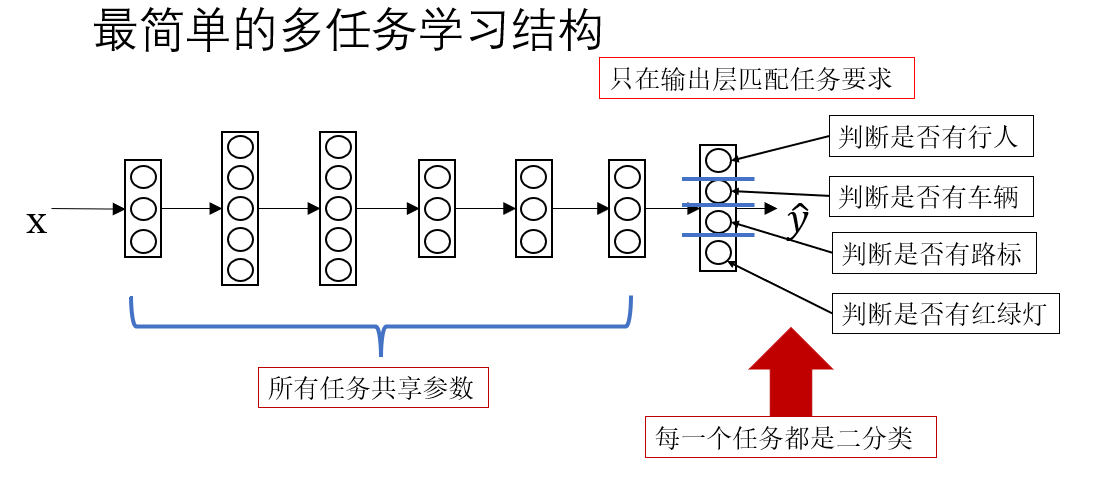
很顯然,這和我們之前的模型並沒有什麼區別,只是根據任務要求給輸出層的每個節點匹配了不同的語義。實際上,在真正的多任務學習裏,這種結構略顯簡陋。
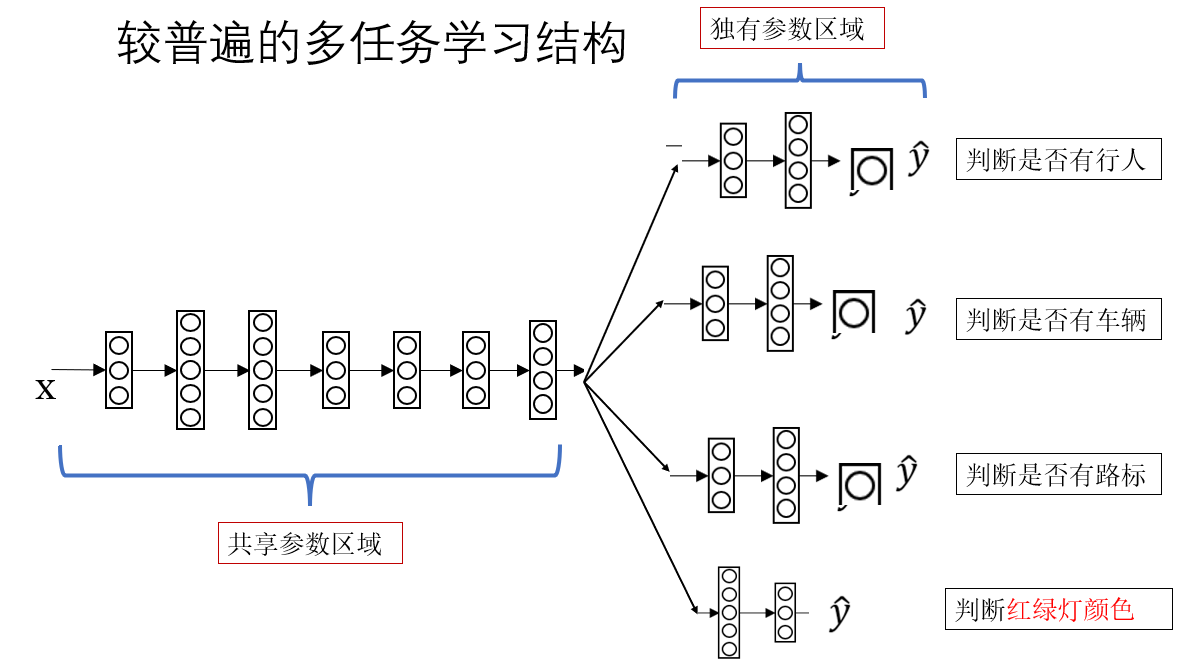
現在我們來看下一步擴展:
這種結構就是和上面的最大區別就在於這種“前面共享、後面分頭”的結構。
模型最前面的幾層負責提取底層特徵,之後,不同任務會接上不同的“小網絡模塊”,我們稱為 task head(任務頭)。
在這裏就是:
- 行人檢測 head:判斷有沒有行人
- 車輛檢測 head:判斷有沒有車
- 路標檢測 head:判斷是否存在路標
- 紅綠燈 head:做紅/黃/綠的分類
這四個任務頭不會共享參數,它們各自學習怎麼從底層特徵裏找出與自己任務相關的特徵。
所以多任務結構能帶來:
- 訓練更快(底層共享)
- 泛化更強(任務間互相幫助)
- 對少數據任務更友好(能借其他任務的信息)
繼續打比方:
模型前面像一位“通識教育老師”教基礎知識;
模型後面像四位“專業課老師”分別教行人檢測、車輛檢測、路標識別、紅綠燈識別。
正向傳播説完了,現在來看看反向傳播。
(3)多任務模型的損失函數整合
現在,每個任務都有自己的損失:
而多任務學習的整體目標是同時優化所有任務,因此最終損失通常是:
與此同時,不同任務可能重要性不同,因此有時會給部分任務更大的權重:
你可以把它理解成學生的期末總成績由多門課程的成績共同決定,有的科目是必修,就權重更高。
最後,多任務學習就像一棵樹:
- 根和樹幹:共享的前幾層(基本特徵提取)
- 分叉的樹枝:根據不同任務分成多個 “Head”
- 每個任務的輸出葉子:分類、迴歸或特定目標
因此這種結構也被稱為 Shared-bottom(共享底層)模型。
2.總結
| 概念 | 原理 | 比喻 |
|---|---|---|
| 多任務學習的適用條件 | 多個任務需要共享大量底層特徵;任務之間具有關聯性;數據量有限時共享結構能互相補充。 | 像學生學習語文、歷史、寫作,三者都依賴閲讀能力,因此可以在同一門“基礎課”中打底,再各自深入。 |
| 多標籤(多任務) vs. 獨熱編碼多分類 | 多標籤任務中,每個標籤彼此獨立,可以同時為 1;獨熱編碼多分類具有互斥性,只能出現一個 1。 | 多標籤:一個人可以同時“會游泳、會跑步”;獨熱編碼:一個人“只能是男或女,不會同時是兩者”。 |
| 多任務學習的標籤結構 | 單一標籤由標量變成向量:\(y^{(i)} = (y^{(i)}_1, y^{(i)}_2, \dots)\);互相獨立,各自對應不同的任務頭。 | 就像一次體檢,一項檢查報告裏同時包含身高、體重、視力、血壓,每一項互不干擾。 |
| 共享底層 + 多任務 Head 的結構 | 模型前幾層負責學習共同底層特徵;後面不同 Head 僅負責學習自己任務特有的模式。 | 前面像“通識課老師”教基礎知識;後面像“專業課老師”各自教授專項技能。 |
| 多任務損失函數的組合方式 | 多任務損失通常相加:\(L = L_1 + L_2 + L_3 + \dots\);必要時加入權重:\(L = \alpha_1 L_1 + \alpha_2 L_2 + \dots\)。 | 像期末總成績由語數外等各科成績共同組成,有些科目(如數學)權重更高。 |