此分類用於記錄吳恩達深度學習課程的學習筆記。
課程相關信息鏈接如下:
- 原課程視頻鏈接:[雙語字幕]吳恩達深度學習deeplearning.ai
- github課程資料,含課件與筆記:吳恩達深度學習教學資料
- 課程配套練習(中英)與答案:吳恩達深度學習課後習題與答案
本篇為第四課的第一週內容,1.4到1.5的內容。
本週為第四課的第一週內容,這一課所有內容的中心只有一個:計算機視覺。應用在深度學習裏,就是專門用來進行圖學習的模型和技術,是在之前全連接基礎上的“特化”,也是相關專業裏的一個重要研究大類。
這一整節課都存在大量需要反覆理解的內容和機器學習、數學基礎。 因此我會盡可能的補足基礎,用比喻和實例來演示每個部分,從而幫助理解。
本篇的內容關於卷積參數,就像全連接層有很多參數一樣,卷積也有很多可以調整的地方。
1. Padding
Padding 的中文可以翻譯為“填充”,但實際在學術和技術討論中,大部分人更習慣於使用英文原詞,尤其是在編程和文獻中,“Padding”已經成為一個標準術語。
在正式介紹 Padding 前,我們先對卷積中的一些基本參數進行符號説明,好方便之後使用。
1.1 卷積的基本符號表示
來看一下卷積中的一些基本表示:
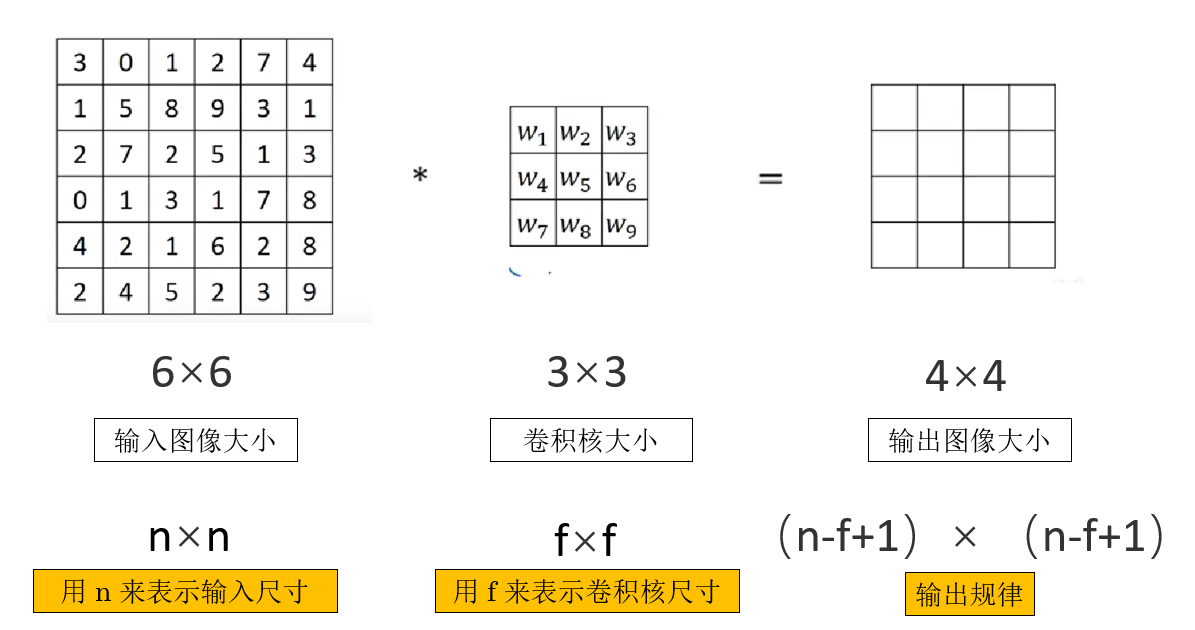
如圖所示,再簡單列舉一下:
- \(n\) 表示輸入特徵圖的空間尺寸(通常指寬或高)。
- \(f\) 表示卷積核的尺寸(同樣指寬或高)。
而經過一層最基本的卷積操作,我們可以發現輸出圖像的尺寸可以表示為:
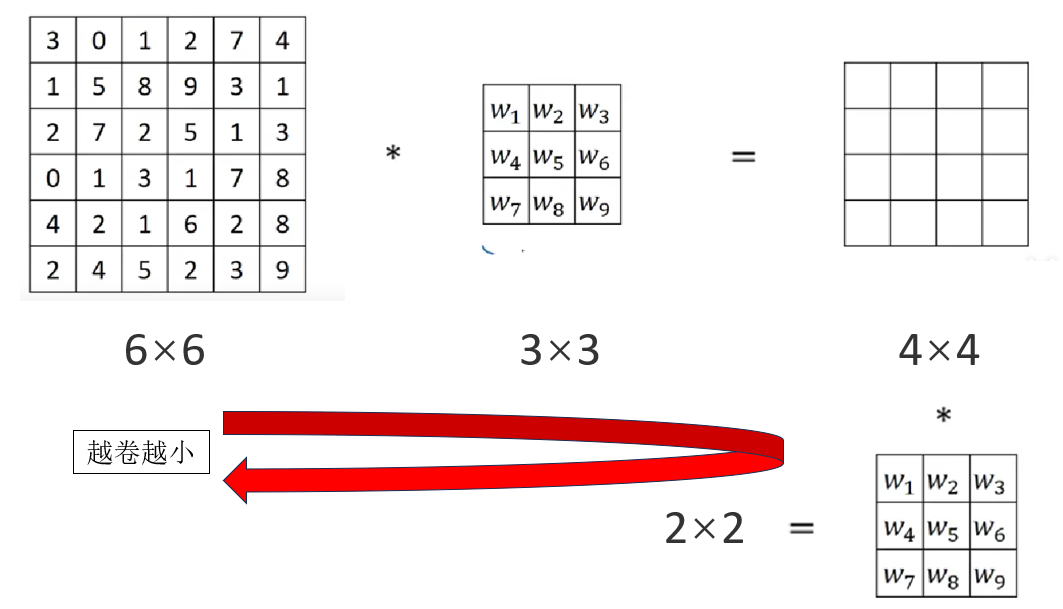
但是這樣就會出現一個問題:我們通過卷積核來提取特徵,會讓圖片變小。
就像對一篇文章進行概括,概括一次讓 100 個字變成 20 個字,再概括一次就成 5 個字,再概括就只剩下 1 個字了。
一個“好”或者“壞”,真的能展示一整篇文章的內容嗎?
卷積也是同樣的道理,如果不進行處理,那麼卷積就會讓圖片不斷變小,信息丟失。
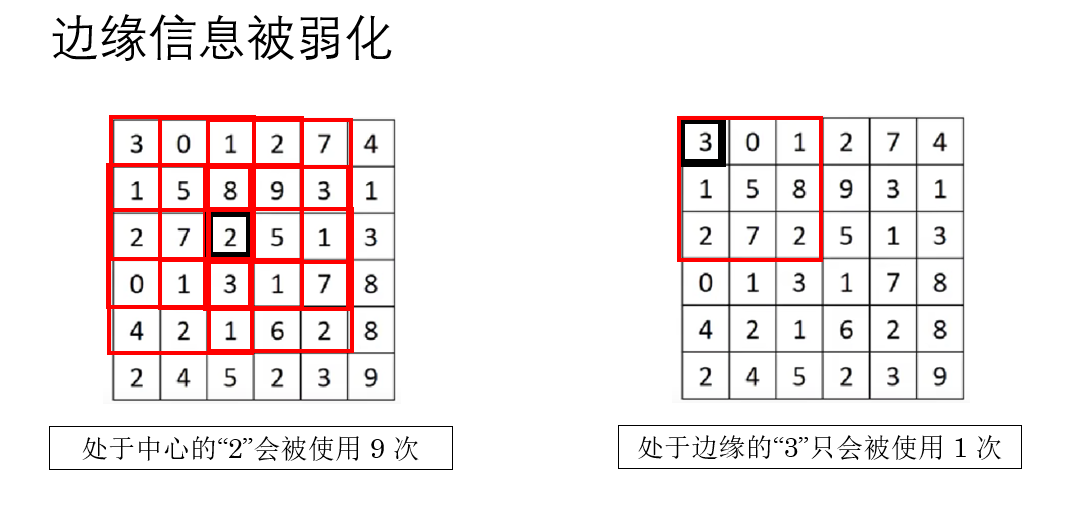
此外,還有一個問題:每個像素的使用不平均,邊緣信息被更少的掃描了。
卷積核在滑動時,只能完全覆蓋在圖像內部的位置,邊緣那一圈天然“吃虧”,被卷積核掃過的次數更少。
如何解決這些問題?答案就是 Padding 。
1.2 什麼是 Padding ?
用英文聽起來可能有些高大上,但 Padding 的邏輯很簡單:既然邊緣不夠大,那就在四周“墊一點東西”進去。
簡單來説:就是圍着輸入圖像再加上一圈或幾圈像素。
現在便在引入一個新的符號規範:
我們用 \(p\) 表示 Padding 的大小,用於説明在圖像四周填充了多少像素。
而對於用什麼填充,也有一些相應的方法:
- 在圖像四周增加 0 值像素(稱為 zero padding)
- 或者根據某些規則複製原圖邊緣的像素
我們就用 zero padding 來演示:
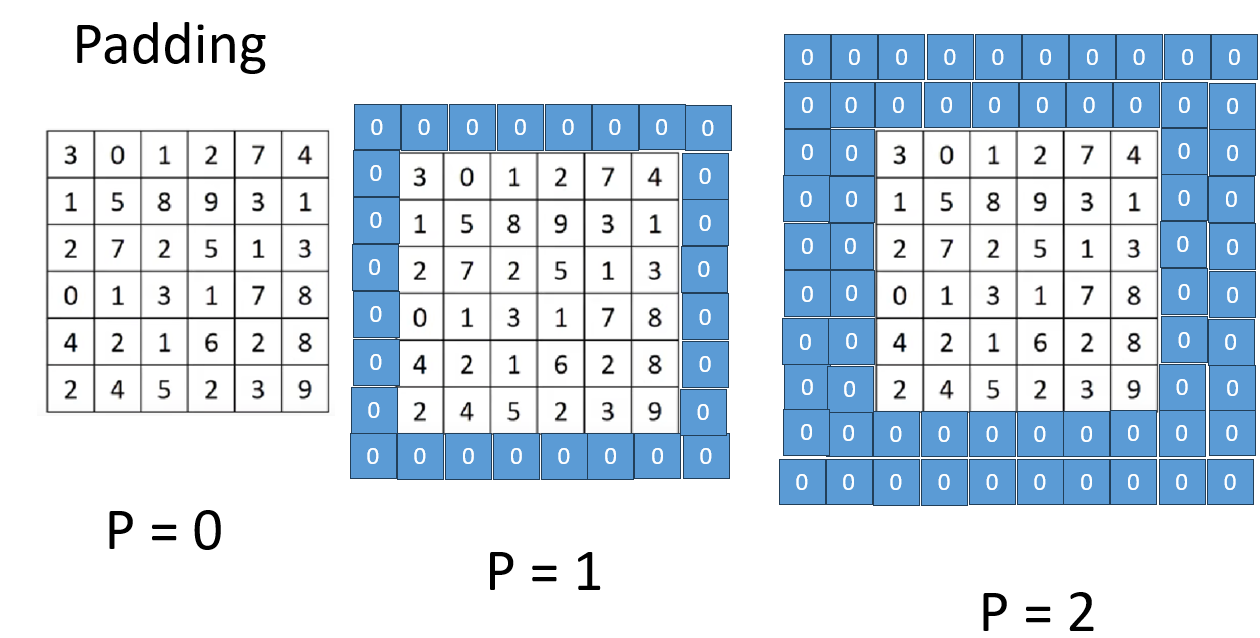
同樣,你會發現 \(p\) 的增加有這樣的規律:
因此,在加入 Padding ,我們就會再次更新從輸入尺寸到輸出尺寸的公式:
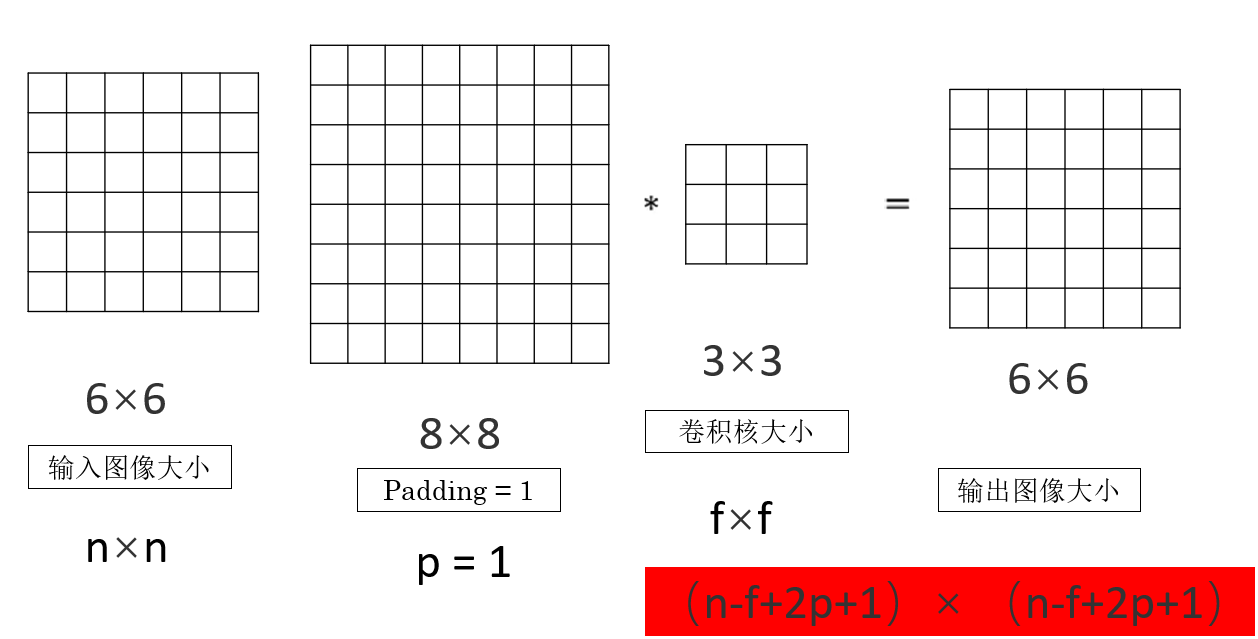
現在,輸出圖像的一邊尺寸就變成了:
這樣,圖片變小和邊緣使用少的問題就都會得到改善。
繼續下一部分。
1.3 valid 卷積和 same 卷積
這是兩種在 Padding 有所區別的卷積方式,簡單介紹一下:
(1)valid 卷積(無填充)
“valid” 的字面意思是“有效的”。
對應到我們前面的符號,就是:
於是輸出尺寸就還是:
這類卷積常用於希望逐步壓縮空間尺寸、提取更抽象特徵的網絡結構中。
(2)same 卷積(輸出與輸入同尺寸)
“same” 的意思是希望輸出與輸入在空間尺寸上 保持一樣大。
為了維持尺寸不變,我們必須人為加 Padding,讓這個公式成立:
整理得到:
這也是為什麼裏卷積核常用 奇數尺寸(如 3、5、7),因為奇數能讓 \(p\) 剛好取整數,否則 same 卷積就無法實現。
same 卷積的意義是:讓每一層都在提取特徵的同時,不縮小空間尺寸,從而保留更“密集”的空間細節。 這也是我們在卷積網絡中普遍選擇的卷積方式。
對於 Padding 部分就先到這裏,接下來看看另一個參數:步長。
2. 卷積步長(stride)
卷積除了 “卷積核大小” 和 “Padding 要不要填” 外,還有一個非常關鍵的參數:步長 stride。如果説卷積核是在“看圖”,Padding 是在“補圖”,那 stride 就決定了它“走路的方式”。
簡單來説,stride 控制的是:卷積核每次滑動時,移動多少格。
繼續引入一個符號規範:
我們用 \(s\) 表示 stride 的大小,用於説明卷積核每次滑動時移動的距離。
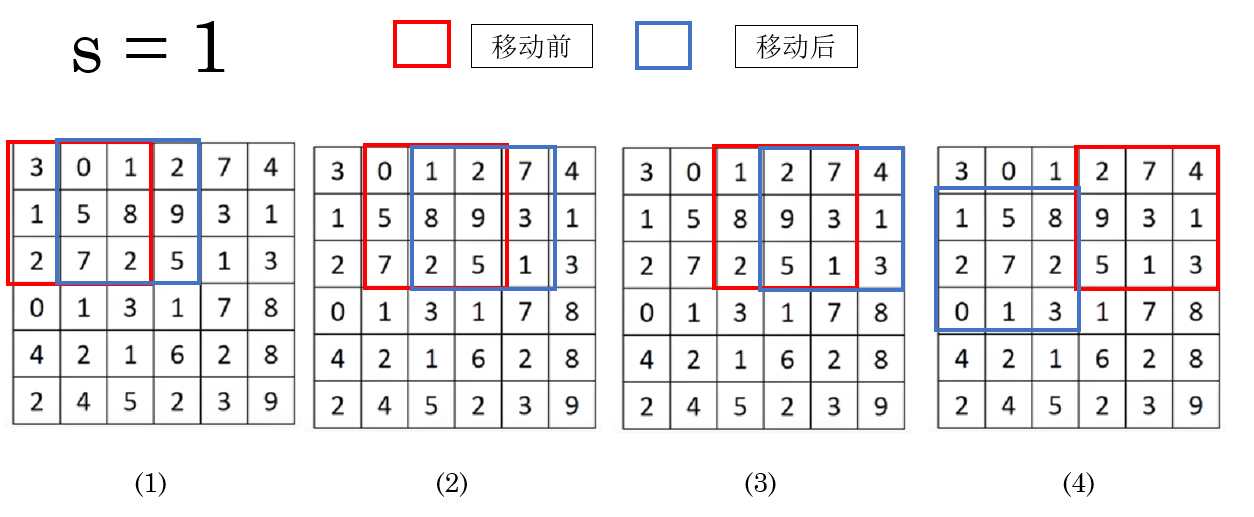
之前的內容裏,實際上 stride 一直存在,在默認情況下,它的值是:
意思是:每次往右或往下移動 1 個像素。
就像你在看一本小説,每翻一頁都要翻到緊挨着的下一頁,這樣你不會漏掉任何內容。
但如果把 stride 調大,比如:
那就變成每次跳兩個格子再看下一塊區域。
就像你看畫冊時,每次跳着翻兩頁——信息當然會變“稀疏”一些。
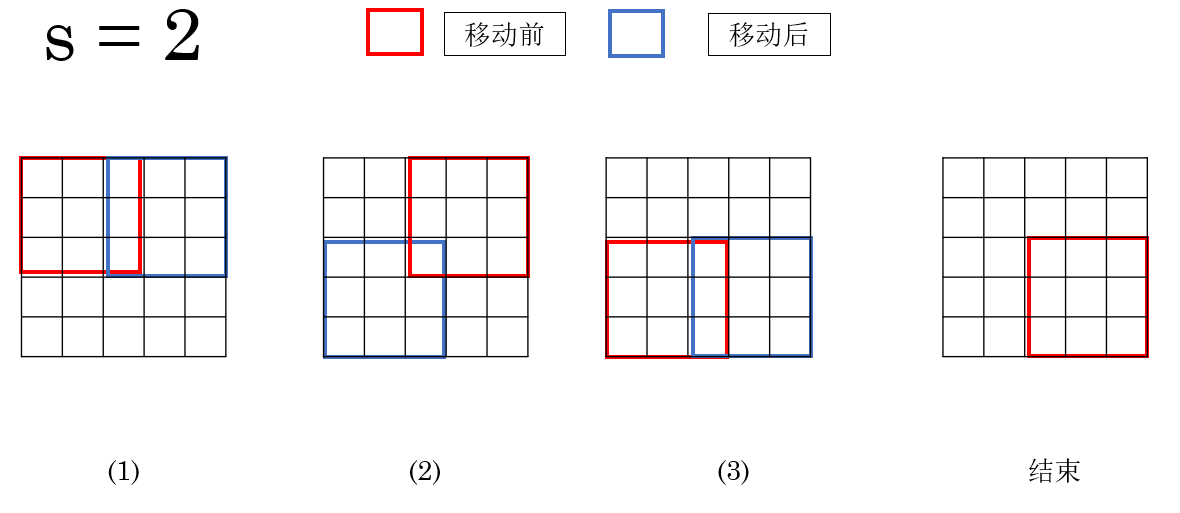
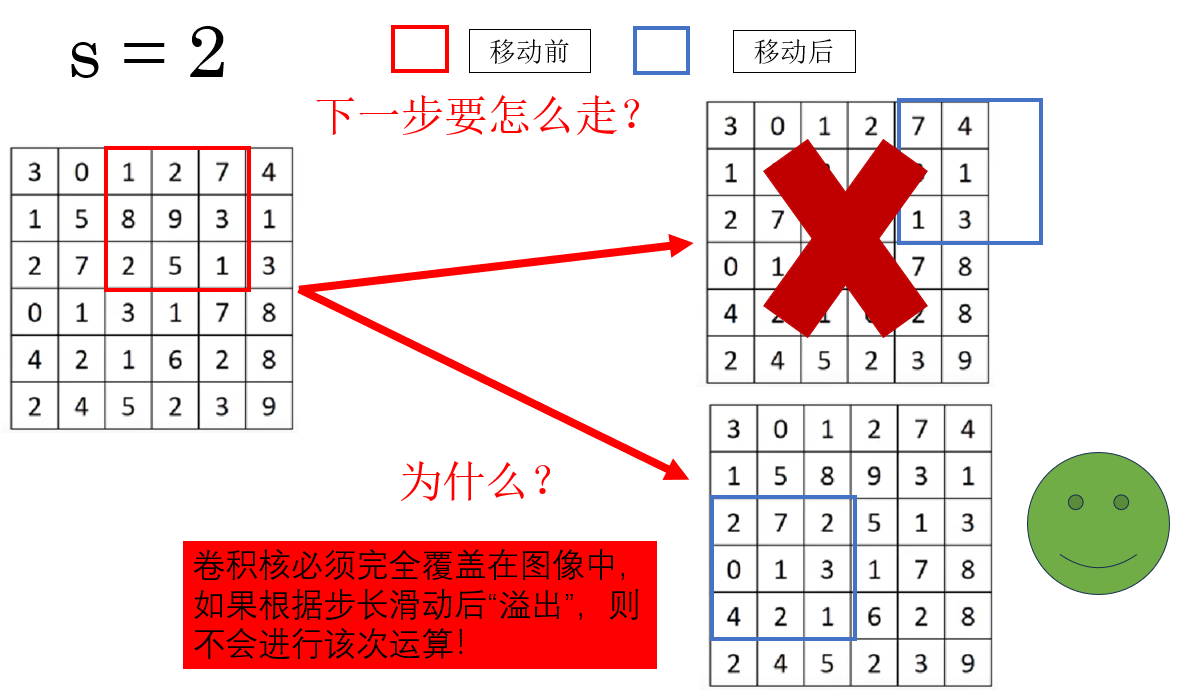
但是當步長增加時,也會出現一種新的情況:
當卷積核有部分移動到圖像外時,就不進行該次卷積運算,而是繼續滑動至下一個完全覆蓋位置或者結束。
實際上,\(s = 1\) 時也是這個邏輯。
因此,這副圖像的卷積過程是這樣的:
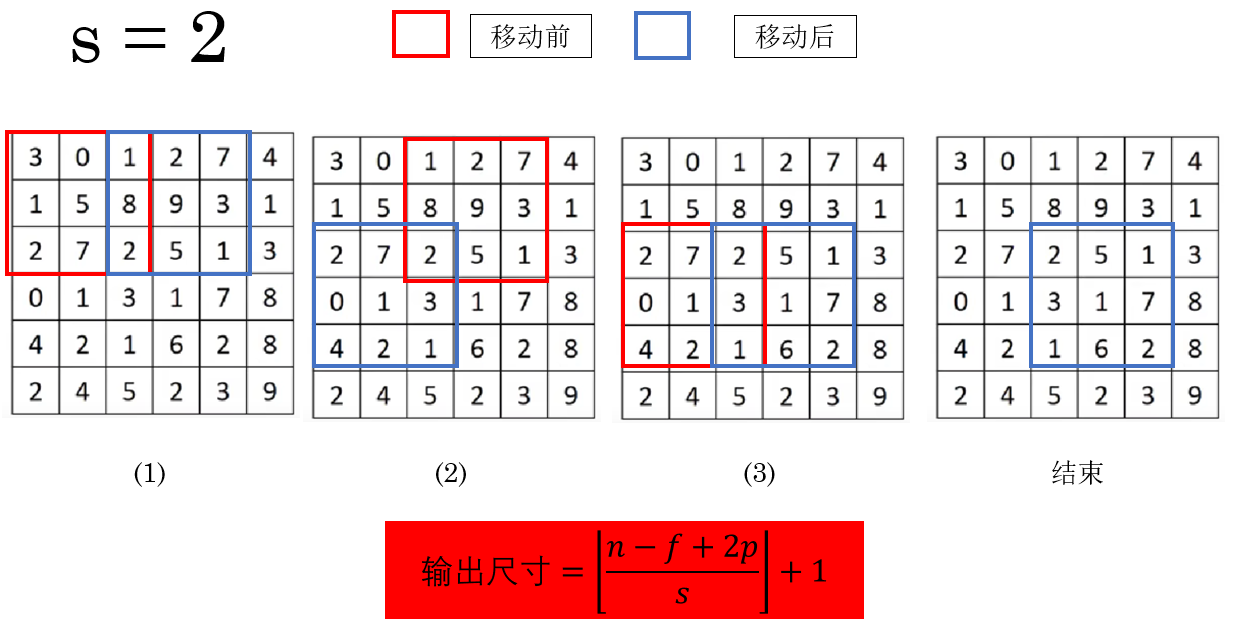
而 stride 的調整也會改變輸出特徵圖的尺寸,輸出公式也要隨之更新:
同時你會發現,在上圖中,如果不進行“溢出”運算,會讓一部分像素丟失。
因此,選擇 \(f\) 與 \(s\) 時儘量保證輸出尺寸為整數,或顯式使用 padding 使其對齊。
總結一下:
- s 越大,輸出越小,計算量越小,感知範圍越大。
- s 越小(最常見是 1),輸出保留更密。
這便是卷積的另一個參數:步長 stride。
這一節課程中額外補充了一點:在數學裏,卷積並不是上面這樣的相乘相加,它在此前會進行一步翻轉,我們進行的卷積在數學裏叫做互相關。
但是在深度學習裏,我們省略了這一步驟,因為我們的卷積核是不斷更新的,我們在慣例,在論文裏的卷積操作指的就是我們上面所介紹的。瞭解就好,就不再展開了。
3. 總結
| 概念 | 原理 | 比喻 |
|---|---|---|
| Padding(填充) | 在輸入圖像四周補上 \(p\) 層像素,使卷積核能在更多位置滑動;解決輸出變小、邊緣利用不足的問題。輸出尺寸公式:\(n-f+2p+1\) | 像給白板貼邊框,讓貼紙(卷積核)能貼到更靠外的區域,不要讓邊緣吃虧。 |
| valid 卷積 | 不做填充,\(p=0\),輸出會變小:\(n-f+1\) | 像剪紙時只剪“能完整落在紙上的圖案”,邊緣那點不夠大的就不要了。 |
| same 卷積 | 通過設置 \(p=\frac{f-1}{2}\) 讓輸出尺寸保持與輸入一樣大。必須使用奇數卷積核尺寸。 | 像在桌面四周加墊子,讓桌布(卷積結果)鋪好後剛好和原桌面一樣大。 |
| stride(步長) | 卷積核每次移動的距離,用 \(s\) 表示。決定卷積核的掃描密度。輸出尺寸公式:\(\left\lfloor\frac{n-f+2p}{s}\right\rfloor+1\) | s=1 是逐格檢查;s=2 是“隔一個掃一個”,像翻相冊時跳着看。 |
| stride 與信息保留 | s 越大,輸出越小、計算更省,但特徵更稀疏;s 越小,信息保留越多。 | 像在地上畫方塊跳格子:跳得越大,踩到的格子越少。 |
| 為什麼卷積要向下取整 | 卷積核必須完全落在圖像內才能計算,溢出部分不做卷積,因此輸出尺寸要取 \(\lfloor\cdot\rfloor\)。 | 像在桌子上擺杯墊,必須完全落在桌面上才能放,否則就算不進去。 |
| 卷積 vs 數學卷積 | 數學中的卷積會翻轉核,但深度學習裏省略這步,直接做“互相關”,因為核會被訓練。 | 像做飯時直接根據口味調整調料,不一定非要照傳統食譜翻鍋步驟。 |