一點前言:之前完成了吳恩達深度學習的相關內容,最近忙於畢設,更新可能沒之前那麼頻繁。這個新開的分類關於模型評估的各種指標的詳解,之前翻看書籍總是被一堆很官方化的概念和密密麻麻的符號搞的看不下去,因此,這次的中心思想是以儘可能通俗的語言、精簡的篇幅來講解這類概念並輔以實例。
不多廢話,以下為正文。
1. 檢測問題中的“兩難情景”
假設我們在機場負責安檢。任務很簡單:把攜帶危險物品的人攔下來。
但現實遠沒有這麼簡單,如果我們把安檢標準定得非常嚴格——一點可疑都不放過,那麼確實可以攔下幾乎所有危險人員。
但代價是,正常旅客也會被頻繁攔下複檢,隊伍排到大廳外。
而如果我們把標準放寬——只在非常明顯的情況下才攔人,旅客通行效率會提高。
但顯然,這就有更大可能漏掉真正的風險。
這就是一個經典的兩難:選擇殺錯還是放過?
抓得越多,錯抓也越多。
抓得越少,漏抓就越多。
目標檢測問題本質上也是如此,在高光譜目標檢測、雷達探測、異常檢測等目標檢測任務中,我們面對的不是“對或錯”這麼簡單,而是在任務情景中,對“錯報”和“漏報”的權衡選擇:
我的模型,能檢測出多少真實目標?但同時會誤報多少背景?我的任務要求我更偏向哪邊?在哪裏二者較為均衡?
總之,在檢測系統中,沒有免費的午餐:提高檢測率,往往要付出虛警率的代價。
ROC 曲線描述的,正是這兩者之間的關係。
2. ROC(Receiver Operating Characteristic)
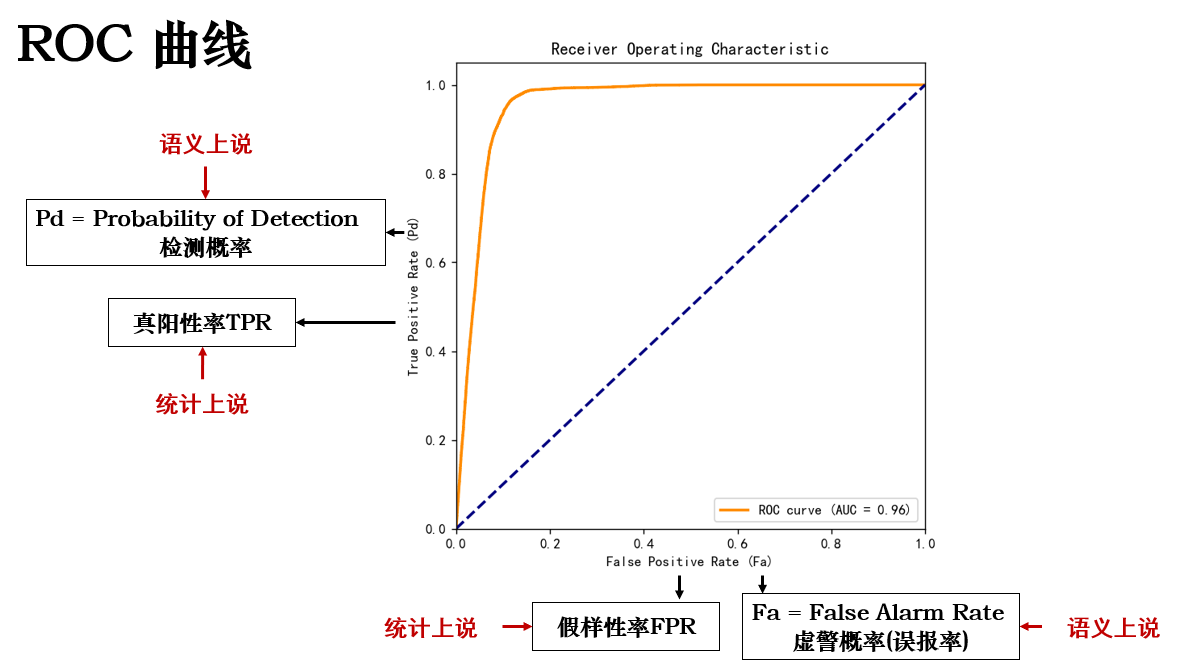
ROC 的英文全稱為 Receiver Operating Characteristic ,直譯為受試者工作特徵曲線,它來源於統計學中的檢測理論,而最早的應用領域是雷達探測。
不同於一些常見指標,ROC 刻畫的是虛警概率和檢測概率間的函數關係。
直接來看一個實例:
現在,假設一天有 100 個攜帶危險物品的旅客和 1000 個普通旅客:
1.真陽性率(TPR / Pd):系統能正確抓住真正危險旅客的比例,即“該抓的抓了多少”。
2.假陽性率(FPR / Fa):系統把普通旅客誤判為危險旅客的比例,即“不該抓的抓錯了多少”。
| 普通旅客數量 | 危險旅客數量 | 通過 / 正常數量 | 抓到數量 | 指標及計算過程 |
|---|---|---|---|---|
| — | 100 | 3 漏掉 | 97 抓到 | 真陽性率 Pd = 97 / 100 = 0.97 (97%) |
| 1000 | — | 800 正常通過 | 200 誤抓 | 假陽性率 Fa = 200 / 1000 = 0.2 (20%) |
實際上二者的計算還是對四類基礎統計量的應用。
這樣,我們就得到了 ROC 曲線中的一個點:\((0.2,0.97)\) ,我們稱之為Pd @ Fa 或 Pd / Fa ,它説明了在特定虛警率下能抓到多少目標,展開如下:
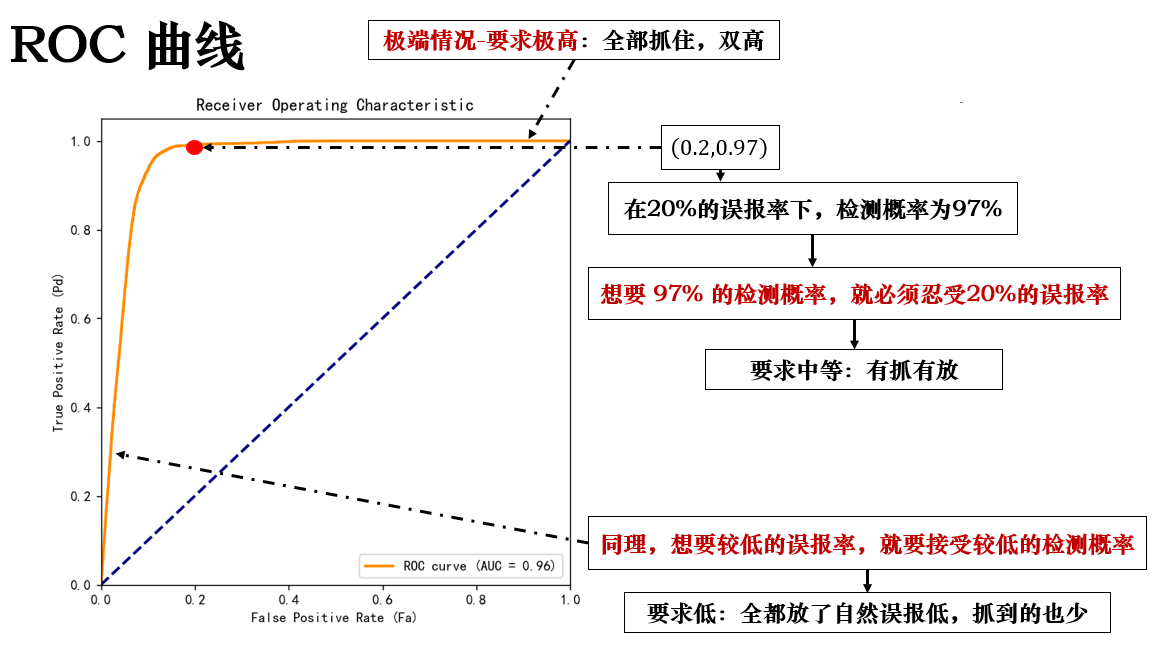
到這裏,就會發現: ROC 曲線中的一個點就是一種決策閾值下的模型表現。
我們不斷測試不同的閾值計算,最終就會得到 ROC 曲線,列舉幾種情況如下:
| 閾值 t | 判定規則 | 危險旅客抓到情況 (Pd) | 普通旅客誤抓情況 (Fa) | 説明 |
|---|---|---|---|---|
| 0.8 | 只有概率 ≥ 0.8 判為危險 | 80 / 100 = 0.80 | 50 / 1000 = 0.05 | 嚴格判定,只抓最明顯的危險旅客,虛警很少 |
| 0.5 | 概率 ≥ 0.5 判為危險 | 95 / 100 = 0.95 | 200 / 1000 = 0.20 | 中等判定,抓到大部分危險旅客,虛警適中 |
| 0.3 | 概率 ≥ 0.3 判為危險 | 99 / 100 = 0.99 | 400 / 1000 = 0.40 | 寬鬆判定,幾乎抓到全部危險旅客,但虛警明顯增加 |
| 0.1 | 概率 ≥ 0.1 判為危險 | 100 / 100 = 1.00 | 800 / 1000 = 0.80 | 極度寬鬆,抓到全部危險旅客,但絕大部分普通旅客也被誤抓 |
觀察下來,你會發現:誤報率越高往往代表閾值越低。
而到了這裏,你可能會有一個問題:那在實際運行中,我總不能一個個閾值去試吧?要多少次才能拼出來完整曲線?
實際上,我們在真實運行中只需要運行一次模型就可以得到完整 ROC 曲線。
用一句話概括其算法:存儲模型對每個樣本的輸出概率並排序,從高到低依次確認為正類(抓捕)並計算 Pd @ Fa ,加入圖像。
來看個例子:
| 排名 | 旅客 ID | 是否危險 | 模型概率 p | 挨個抓 | 累計 TP | 累計 FP | Pd = TP / 3 | Fa = FP / 7 |
|---|---|---|---|---|---|---|---|---|
| 1 | A | ✅ 危險 | 0.95 | 抓 | 1 | 0 | 0.33 | 0 |
| 2 | B | ❌ 普通 | 0.90 | 抓 | 1 | 1 | 0.33 | 0.14 |
| 3 | C | ✅ 危險 | 0.85 | 抓 | 2 | 1 | 0.67 | 0.14 |
| 4 | D | ❌ 普通 | 0.70 | 抓 | 2 | 2 | 0.67 | 0.29 |
| 5 | E | ❌ 普通 | 0.60 | 抓 | 2 | 3 | 0.67 | 0.43 |
| 6 | F | ✅ 危險 | 0.50 | 抓 | 3 | 3 | 1.00 | 0.43 |
| 7 | G | ❌ 普通 | 0.45 | 抓 | 3 | 4 | 1.00 | 0.57 |
| 8 | H | ❌ 普通 | 0.30 | 抓 | 3 | 5 | 1.00 | 0.71 |
| 9 | I | ❌ 普通 | 0.20 | 抓 | 3 | 6 | 1.00 | 0.86 |
| 10 | J | ❌ 普通 | 0.10 | 抓 | 3 | 7 | 1.00 | 1.00 |
在這裏,當把旅客F抓捕時,計算得到的 Pd @ Fa 較優,也就是説,其對應的模型概率 p=0.5 就是一個可能較優的決策閾值選擇。
到這裏 ROC 的內容就基本結束,但是你會發現:曲線裏我光看不同閾值的情況了,那這個模型本身到底好不好?有多好?能不能給我一個明確的評估呢?
這就是與 ROC 曲線相關聯的內容:AUC 。
3. AUC(Area Under Curve)
AUC 的全稱是 Area Under Curve,直譯就是ROC 曲線下面積。它用一個單一指標來衡量模型整體能力。
在得到 ROC 曲線後,AUC的計算非常簡單:
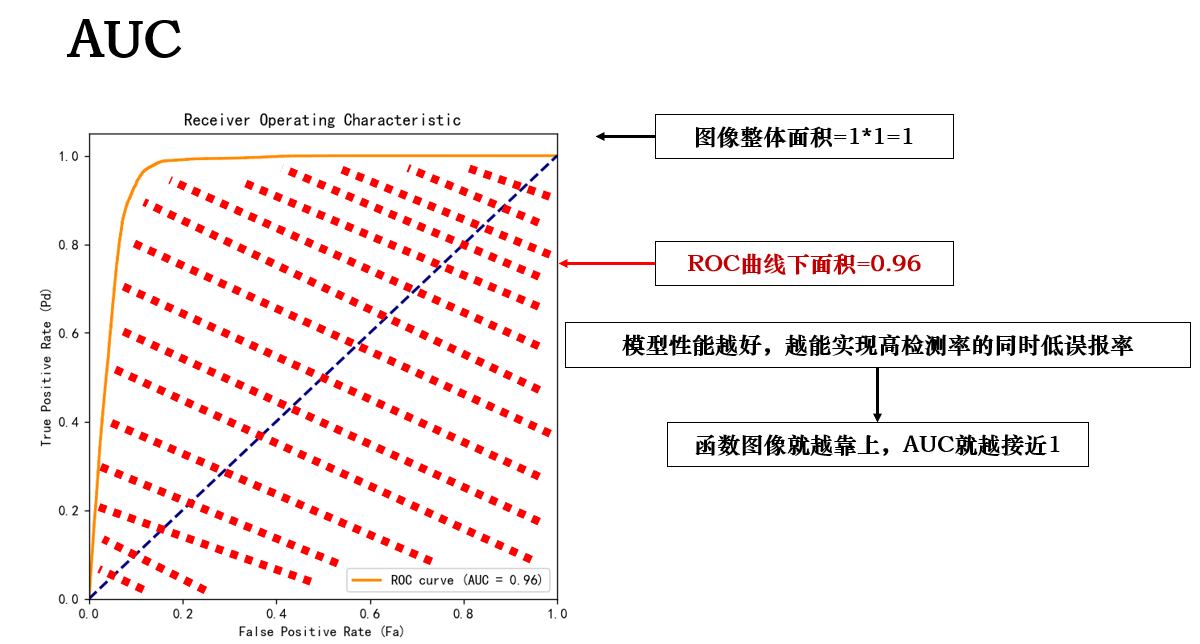
顯然,AUC面積越大,模型越能在低虛警率下實現高檢測率,模型的檢測效果就越好。
並且,我們不需要提前選定決策閾值,就可以知道模型整體的好壞。
總結一句話:ROC 告訴我們在不同標準下模型表現如何,而 AUC 則給出一個整體評分,實現不用盯着每個閾值也能知道模型好不好,從而幫助相關任務的調優和部署。


