此分類用於記錄吳恩達深度學習課程的學習筆記。
課程相關信息鏈接如下:
- 原課程視頻鏈接:[雙語字幕]吳恩達深度學習deeplearning.ai
- github課程資料,含課件與筆記:吳恩達深度學習教學資料
- 課程配套練習(中英)與答案:吳恩達深度學習課後習題與答案
本篇為第五課的第二週內容,2.7的內容以及一些相關知識的補充。
本週為第五課的第二週內容,與 CV 相對應的,這一課所有內容的中心只有一個:自然語言處理(Natural Language Processing,NLP)。
應用在深度學習裏,它是專門用來進行文本與序列信息建模的模型和技術,本質上是在全連接網絡與統計語言模型基礎上的一次“結構化特化”,也是人工智能中最貼近人類思維表達方式的重要研究方向之一。
這一整節課同樣涉及大量需要反覆消化的內容,橫跨機器學習、概率統計、線性代數以及語言學直覺。
語言不像圖像那樣“直觀可見”,更多是抽象符號與上下文關係的組合,因此理解門檻反而更高。
因此,我同樣會儘量補足必要的背景知識,儘可能用比喻和實例降低理解難度。
本週的內容關於詞嵌入,是一種相對於獨熱編碼,更能保留語義信息的文本編碼方式。通過詞嵌入,模型不再只是“記住”詞本身,而是能夠基於語義關係進行泛化,在一定程度上實現類似“舉一反三”的效果。詞嵌入是 NLP 領域中最重要的基礎技術之一。
本篇的內容關於分層 softmax 和負採樣,是用來提升詞嵌入模型訓練效率,節省計算開銷的技術。
1. 分層 softmax
在上一篇介紹 Word2Vec 的時候,我們默認使用的是標準 softmax 來計算輸出層的概率分佈。但如果稍微停下來仔細想一想,就會立刻意識到一個問題:在大詞表場景下,標準 softmax 幾乎是不可用的。
下面我們分點來展開標準 softmax 在詞嵌入中的侷限和分層 softmax 的思想:
1.1 標準 softmax 的計算開銷
在之前的示例中,我們反覆強調過一點:輸出層的神經元個數與詞典大小完全一致。
這是因為,在 Word2Vec 的建模視角下,預測過程本質上可以被看作一個單標籤分類問題:
- 目標詞對應“正確類別”
- 詞表中其餘所有詞都對應“錯誤類別”
因此,我們需要通過 softmax 將模型輸出映射為一個對整個詞表的概率分佈,並在反向傳播階段不斷強化正確預測、抑制錯誤預測。
從建模邏輯上看,這一過程是完全合理的,但真正的問題,並不出在“對不對”,而是“能不能實現”。
我們知道,在 NLP 任務中,如果希望模型具備更強的泛化能力,第一步往往就是擴大語料規模,進而構建更大的詞典。
而當我們希望模型在現實場景中“真正好用”時,其性能指標往往需要不斷逼近,甚至嘗試超越我們之前介紹過的貝葉斯最優錯誤率。
在這個意義上,詞典規模並不是一個可有可無的工程參數,而是模型能力的硬上限。
一個直觀的類比就是:人類的大腦究竟“記住”了多少詞? 顯然,這絕不是一個可以用“幾千”或“幾萬”來描述的數量級。
問題也正是在這裏開始顯現的:對於一次標準 softmax 計算而言,如果詞表大小為 \(|V|\),那麼模型在輸出層需要完成的操作包括:
- 對 \(|V|\) 個詞向量 分別計算內積。
- 對 \(|V|\) 個得分 進行指數運算。
- 對所有結果求和並完成歸一化。
其計算形式可以寫成:
注意,這裏省略了 softmax 輸出層的偏置項,在 Word2Vec 的實際建模與實現中,該偏置對詞向量語義結構的影響通常可以忽略,這是很簡單的道理:我們需要刻畫向量間的距離關係,而偏置帶來的整體平移顯然是沒有意義的。
回到正題,也就是説,哪怕我們只關心一個目標詞的概率, 模型仍然必須對整個詞表中的所有詞各計算一遍打分。
因此,每一個訓練樣本在輸出層的計算複雜度都是:\(O(|V|)\)。
當 \(|V|\) 只有幾千時,這個代價尚可接受,但一旦詞典規模達到幾十萬、甚至上百萬級別,這一步計算就會迅速成為訓練過程中的主要瓶頸。
換句話説,標準 softmax 的計算成本與詞表規模線性相關,這一性質在大詞表場景下是無法迴避的。
用我們之前的內容來類比一下:你見過幾百萬類別的分類模型嗎?
也正是在這樣的背景下,我們不得不思考新的問題: 可不可以在不顯式遍歷整個詞表的前提下,完成對目標詞的有效建模?
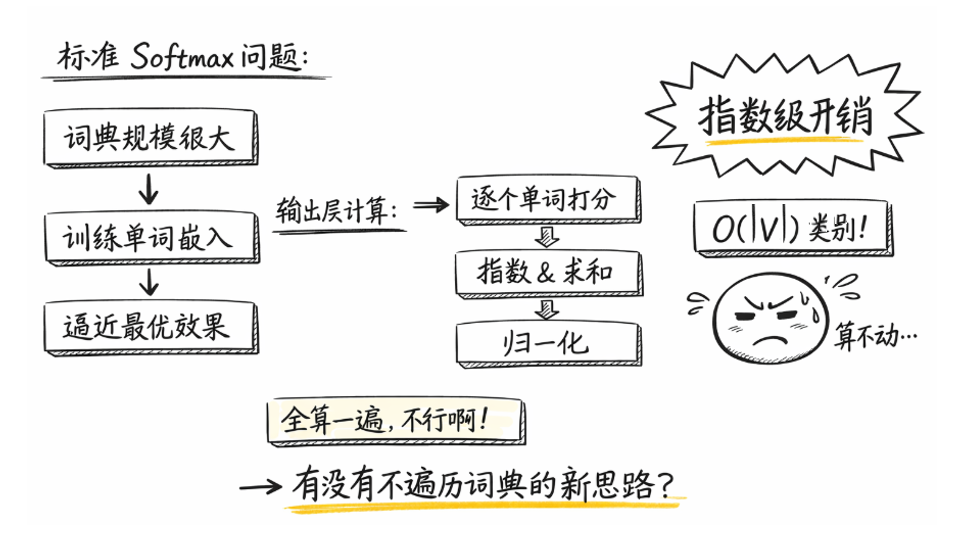
於是,Word2Vec 提出了第一種加速策略:分層 softmax。
1.2 哈夫曼樹
哈夫曼是其實是數據結構裏的內容,我們看看它在分層softmax中實現的效果。
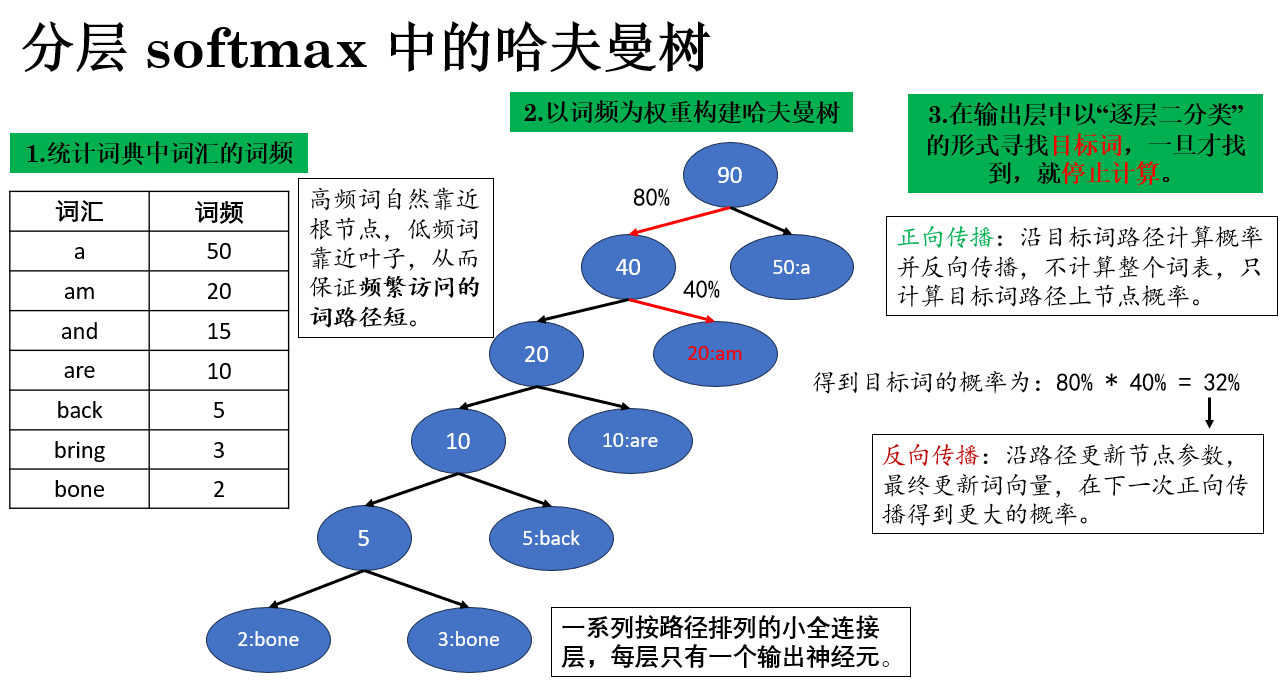
哈夫曼樹最早被用於無損數據壓縮,其核心思想可以概括為一句話:出現頻率越高的符號,編碼越短;出現頻率越低的符號,編碼越長。 通過這種方式,高頻符號擁有更短的路徑長度,從而在整體意義下最小化編碼的期望長度。
在 分層softmax 中,並沒有使用其壓縮編碼的邏輯,而是重點利用哈夫曼樹中高頻符號擁有更短的路徑長度的特點來組織詞表並優化傳播邏輯,它的過程如下:
再具體來説,Word2Vec 的分層 softmax 將詞表組織成哈夫曼樹的步驟如下:
- 統計詞頻:首先對語料庫中的每個詞計算出現頻率,頻率越高的詞表示越常見,也就越可能在訓練中被訪問多次。
- 構建哈夫曼樹:
- 將每個詞作為葉子節點,節點權重 = 詞頻;
- 從最小權重的兩個節點開始合併,生成新的父節點,權重為子節點權重之和;
- 重複此過程,直到只剩下根節點。
通過這種方式,高頻詞自然靠近根節點,低頻詞靠近葉子,從而保證頻繁訪問的詞路徑短。
- 路徑作為概率計算序列:
- 每條從根到葉子的路徑對應一次概率計算的序列:每個節點上的選擇可以看作一次二分類(是否沿左/右分支走)。
- 目標詞的概率 = 路徑上所有二分類概率的乘積。
- 降低訓練開銷:
- 高頻詞路徑短 → 更新梯度的節點少 → 每次訓練樣本計算量小。
- 低頻詞路徑長 → 雖然節點多,但訓練中出現頻率低,對整體訓練開銷影響小。
- 整體而言,平均計算複雜度從 \(O(|V|)\) 降到 \(O(\log |V|)\),極大提升了大詞表場景下的訓練效率。
只看到這裏,可能還是有些模糊,我們以 CBOW 為例,來看看使用分層 softmax 的整體網絡結構和傳播過程。
1.3 CBOW 中的分層 softmax
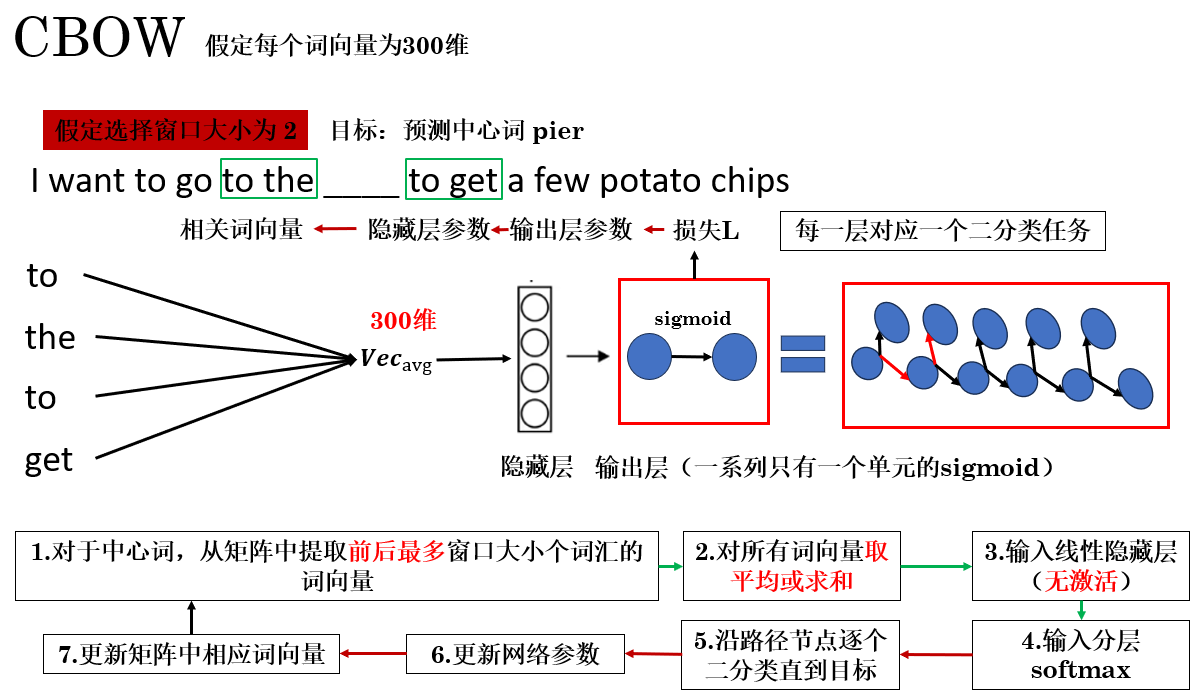
這樣,最終效果是:一個原本包含幾百萬類別的輸出問題,被分解成了一系列二分類問題。
在每次訓練時,網絡只需更新目標詞路徑上的相關節點參數,而不必觸及整個輸出層,從而大幅節省計算開銷。
同時,由於哈夫曼樹天然按照詞頻組織,高頻詞位於靠近根節點的路徑上,使得這些詞的更新路徑更短、訪問更快。這不僅加速了高頻詞的學習,也讓整體訓練過程更加高效。
這便是分層 softmax 的原理,如果從實際應用上來説,你也可以叫它”堆疊 sigmoid“,而 CBOW 便常常和分層 softmax 搭配使用。
下面我們便來看看另一種加速策略:負採樣。
2. 負採樣(Negative Sampling)
如果説分層 softmax 是一種結構層面的加速,那麼負採樣更像是一種從目標函數層面“改問題”的方法。
它的出發點非常直接:我們真的有必要在訓練時區分“目標詞”和“所有非目標詞”嗎?
答案是:不需要。
相較於分層 softmax,負採樣的思想更加樸素、實現也更加簡單。在實際工程中,它幾乎可以看作是 Skip-gram 的默認搭檔,也是 Word2Vec 最常被使用的訓練方式之一。
負採樣的核心思想可以概括為一句話:只挑選少量負樣本進行訓練,而非遍歷整個詞表。換句話説,我們只關心“正確詞 + 一些隨機挑選的錯誤詞”,其他的全體詞不參與計算。
這樣,計算量從 \(O(|V|)\) 直接降到了 \(O(k)\),其中 \(k\) 是負樣本的數量(通常 \(5 \sim 20\))。
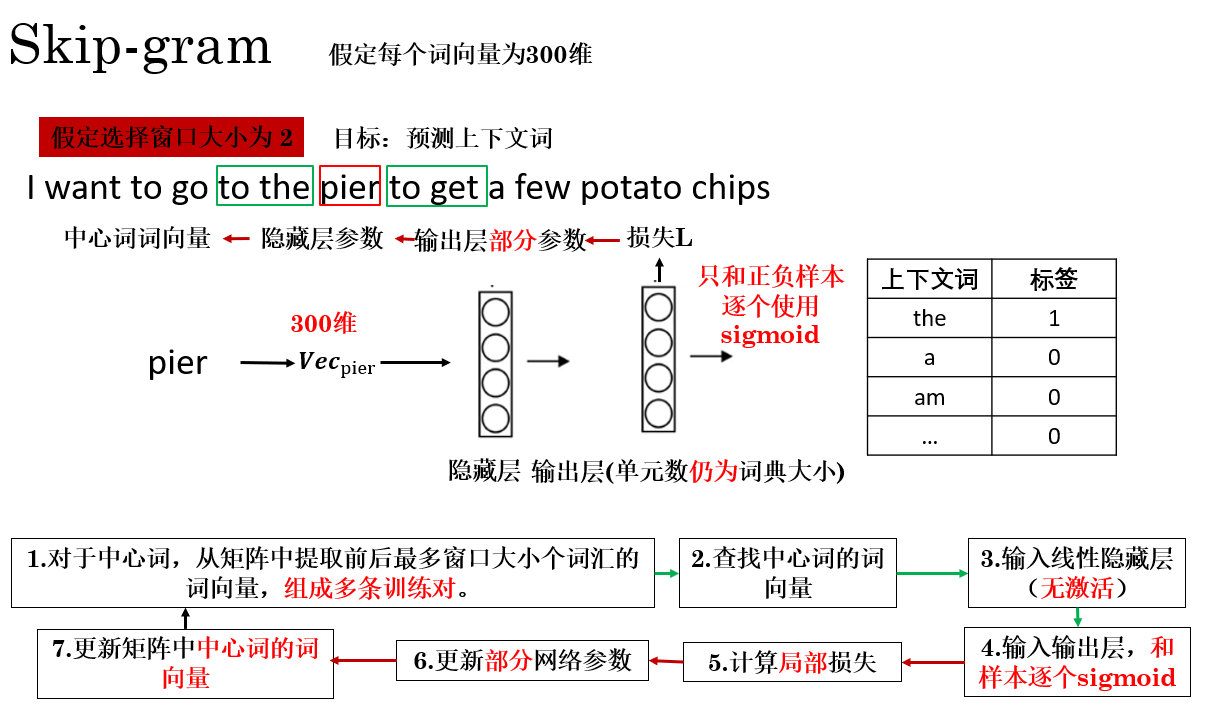
我們以 Skip-gram 為例來演示負採樣的原理:
2.1 確定正負樣本
使用負採樣的第一步是確定正負樣本,這一過程同樣容易理解,來看看:
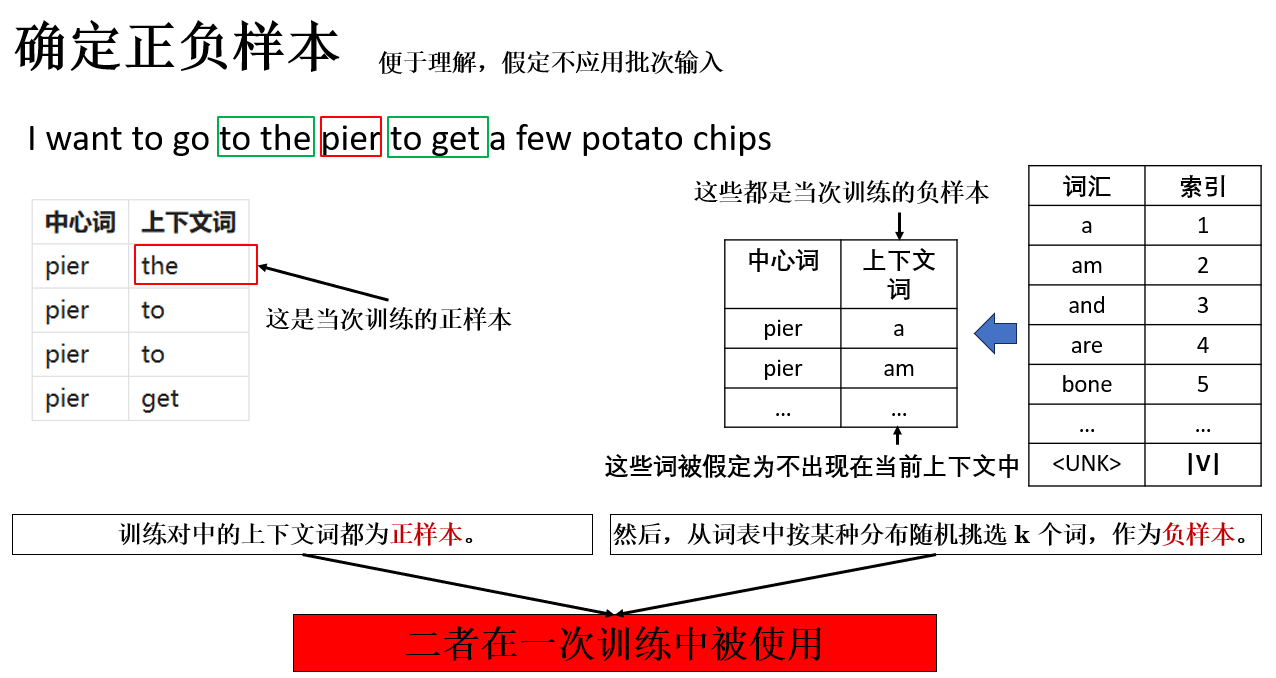
其中:
- 正樣本:由真實語料中出現的上下文詞構成;
- 負樣本:從詞表中隨機抽取,但並不出現在當前上下文中的詞。
這裏展開一點,對於負樣本的採樣,我們常常使用下面這個公式:
- \(P(w)\):表示在負採樣中抽到詞 \(w\) 的概率。
- \(U(w)\):表示詞 \(w\) 在整個語料庫中的出現頻率。
- \(\propto\):表示“與……成正比”,意思是我們先按這個規則給每個詞一個權重,再歸一化成概率。
語言描述就是:先算每個詞的詞頻的四分之三次方,然後把它們除以所有詞的詞頻的四分之三次方 之和,就得到最終抽樣概率 \(P(w)\):
這個公式實際上做的是這樣的工作:
- 對高頻詞做了降權(比原始詞頻低一些),減少它們在負樣本中出現的概率。
- 對低頻詞做了相對提升(比直接按詞頻高一些),讓它們有機會被採樣到。
這種採樣策略在實踐中被證明可以提高詞向量訓練的穩定性和語義表達能力。
完成了數據準備後,現在,就來看看 Skip-gram 中的負採樣。
2.2 Skip-gram 中的負採樣
在 Skip-gram + 負採樣 框架下,一次訓練的傳播過程可以概括為下圖所示:
這種思路其實很容易理解:在一次傳播中,我不再一次更新輸出層的所有參數,而是隻計算我提前挑選好的一些樣本,只更新它們相關的參數,來節省計算開銷,剩下的等下次選中再更新。
最終,模型僅更新正樣本和 \(k\) 個負樣本對應的輸出層參數以及輸入詞向量,其餘詞的向量完全不參與更新,從而節省了大量計算,實現 \(O(k)\) 的複雜度,遠小於 \(O(|V|)\)。
這種“只更新被選中參數”的訓練方式,使得負採樣在大規模語料與超大詞表場景下,具備極高的計算效率。
你會發現,負採樣和分層 softmax 的一點共同邏輯就是把一次多分類拆成了多次二分類,這同樣是我們可以學習的優化思路。
3.總結
| 概念 | 原理 | 比喻 |
|---|---|---|
| softmax大詞表瓶頸 | softmax 的計算與反向傳播都必須遍歷整個詞表,詞表越大,訓練越慢,成為主要性能瓶頸 | 在問路時,必須問完全國所有居民 |
| 分層 softmax | 用哈夫曼樹將多分類問題拆成一條從根到葉的二分類決策路徑,目標詞概率等於路徑上各二分類概率的乘積 | 在每個路口選擇方向,而不是一次問遍所有人。 |
| 分層 softmax +CBOW | 每次訓練只更新目標詞路徑上的節點參數,其餘詞完全不參與計算 | 只維修你真正經過的路口,而不是重修整座城市。 |
| 負採樣(Negative Sampling) | 不再逼模型區分“目標詞 vs 全詞表”,而是區分“目標詞 vs 少量噪聲詞”,複雜度為 \(O(k)\) | 不用認清所有陌生人,只要確認朋友和幾名路人 |
| 正負樣本構造 | 正樣本來自真實上下文;負樣本從詞表隨機抽取但不在上下文中 | 真朋友 vs 隨機拉來的假熟人 |
| \(U(w)^{3/4}\) 採樣分佈 | 對高頻詞降權、對低頻詞相對提升,使負樣本更有信息量 | 熱門明星少出現點,路人多給點鏡頭 |
| Skip-gram + 負採樣 | 每次僅更新中心詞、正樣本詞和 \(k\) 個負樣本的向量,其餘參數不動 | 只訓練被點名的幾個人,其他人下次再説 |