此分類用於記錄吳恩達深度學習課程的學習筆記。
課程相關信息鏈接如下:
- 原課程視頻鏈接:[雙語字幕]吳恩達深度學習deeplearning.ai
- github課程資料,含課件與筆記:吳恩達深度學習教學資料
- 課程配套練習(中英)與答案:吳恩達深度學習課後習題與答案
本篇為第二課第一週的內容,1.10到1.14的內容,也是本週理論部分的最後一篇。
本週為第二課的第一週內容,就像課題名稱一樣,本週更偏向於深度學習實踐中出現的問題和概念,在有了第一課的機器學習和數學基礎後,可以説,在理解上對本週的內容不會存在什麼難度。
當然,我也會對一些新出現的概念補充一些基礎內容來幫助理解,在有之前基礎的情況下,按部就班即可對本週內容有較好的掌握。
在瞭解了歸一化後,本週課程最後一部分內容介紹了一些實際運行中的梯度現象和相應的一些處理方法。
要提前説明的是,這部分內容涉及較多的數學基礎。而涉及到的核心概念:梯度檢驗,又因為現在技術的成熟而幾乎不再使用,即使使用,現有的流行框架也都有相應封裝好的方法。
因此,相比課程裏的推公式,我會更偏向減少公式的出現,用實例和比喻來解釋概念,當然,仍會對核心的公式和原理進行解釋。
同樣,如果你希望只瞭解概念及其作用,我會在最後,用一版“人話版總結”來做這部分內容。
1.梯度現象
1.1 梯度爆炸和梯度消失
假設我們有一個 4 層的簡單神經網絡,不設激活函數(或者設為原值)每層權重的平均值是 0.9。
梯度反向傳播時,每經過一層都會乘上該層的導數,大約為 0.9:
梯度稍微變小了一點,這沒問題。
但如果層數再多,比如 20 層:
這時梯度幾乎消失了。
如果再更多層呢?這樣下來,每次參數的更新就會小的幾乎沒有,就像一個步履蹣跚的老人下山,讓模型的學習永無盡頭,這就是梯度消失(vanishing gradient)。
反過來,如果每層平均值是 1.2:
這時梯度變得極大,出現“爆炸”,這樣次次迭代後參數就會像一個超人一樣次次進化,最後飛在天上在整個山谷亂竄,更別説“找谷底”了,這就是梯度爆炸(Exploding Gradient)。
再用一個例子來説明二者在實際運行中的效果:
- 梯度消失:像一連串傳話遊戲,傳到最後只剩耳語,網絡“聽不見”誤差信號。
- 梯度爆炸:像一連串擴音器,每層都加倍音量,最後系統崩潰。
再來看一個實例:
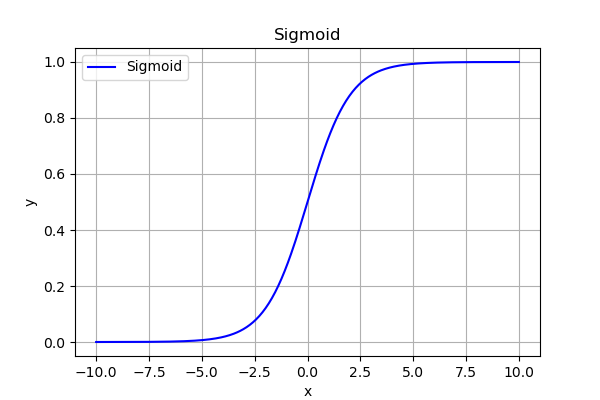
假設現在我們使用 Sigmoid 激活函數:
其導數最大值為 \(0.25\)。
如果網絡有 10 層,那麼誤差信號傳回輸入層的幅度最多為:
幾乎為零。
這就是為什麼深層網絡用 Sigmoid 會難以訓練,我們通常在二分類的輸出層使用它而不是隱藏層的原因之一。
最後總結一下判斷二者的實驗現象:
- 梯度消失:loss 幾乎不下降,權重幾乎不變。
- 梯度爆炸:loss 一直 NaN (not a number) 或突然發散(突然急劇增加)。
而如何避免這種情況產生?很明顯,在數據合理的前提下,我們就要給參數一個合理的初值,讓它在後續更新中既不會太大,也不會太小。
也就是初始化問題,之前在簡單的神經網絡裏,我們學習了隨機初始化,而現在深層神經網絡中,我們也有相應的初始化方法。
1.2 應對二者的權重初始化
梯度之所以不穩定,是因為初始權重太小或太大導致信號在層間放大或縮小。
因此我們希望每一層的輸入和輸出方差保持一致。
好像有些模糊,為什麼方差一致就能讓梯度穩定? 我們由此來展開解釋:
(1)什麼叫“方差一致”?
在神經網絡中,每一層都會對輸入做一次線性變換,看一眼老公式,就不再重複了:
而現在,我們希望:
也就是説,一層輸出的波動幅度(方差)不要比輸入大或小太多。
(2)為什麼方差變化會出問題?
其實這和我們剛剛闡述的梯度現象是一個道理,只是剛剛是用反向傳播説明,現在是用正向傳播説明:
想象每層都稍微放大一點信號(方差增加):
如果有 20 層:
這意味着信號在傳播過程中被放大了 38 倍,
→ 在反向傳播時,梯度也會被同樣放大 → 梯度爆炸。
反過來,如果每層都縮小一點信號(方差減少):
那麼:
→ 信號越來越小,最終接近 0,
→ 梯度反向傳播時也會逐層消失 → 梯度消失。
還是剛剛那個比方:
- 如果每層都“放大”一點,信號越傳越響亮,最後炸麥 → 梯度爆炸;
- 如果每層都“削弱”一點,信號越傳越輕,最後聽不見 → 梯度消失;
- 只有音量穩定傳遞,才能讓整首歌(網絡)正常演奏完。
因此,我們才需要每一層的輸入和輸出方差保持一致。
(3)這和權重初始化的關係
理清楚邏輯後,我們來看看如何通過初始化來實現方差一致:
對於單個神經元:(偏置不影響方差,這裏省去)
假設:
- 每個 \(x_i\) 均值為 0,方差為 \(Var(x_i)=\sigma_x^2\);
- 權重 \(w_i\) 獨立同分布,方差為 \(Var(w_i)=\sigma_w^2\)。
在這些假設下,線性組合的方差是各項方差之和:
又因為 \(w_i\) 與 \(x_i\) 獨立:(這是數學裏概率論部分的知識)
因此:
若我們希望輸出的方差與輸入的方差相同(即方差保持一致),設 \(Var(z) = \sigma_x^2\),則:
最終,我們得出結論:如果輸入方差為 \(\sigma_x^2\) 且滿足上述獨立性假設,那麼把權重的方差設為 \(1/n\)(\(n\) 為該層的輸入維度,也稱 fan_in)可以使輸出方差與輸入方差保持一致。
來看一個具體的例子:
假設 \(fan_{in} = n = 100\),且輸入每個通道方差 \(\sigma_x^2 = 1\)(應用歸一化的結果)。
- 由公式得到\(\sigma_w^2 = 1/n = 1/100 = 0.01\)
- 那麼輸出方差: \(Var(z) = n \sigma_w^2 \sigma_x^2 = 100 \times 0.01 \times 1 = 1\),與輸入方差相等(方差一致)。
若不這麼做,比如 \(\sigma_w = 0.5\)(\(\sigma_w^2=0.25\))更大:
- 輸出方差 \(=100 \times 0.25 \times 1 = 25\) → 被放大 25 倍(梯度爆炸)。
若 \(\sigma_w = 0.01\)(\(\sigma_w^2=1e-4\))更小:
- 輸出方差 \(=100 \times 1e-4 = 0.01\) → 被縮小(梯度消失)。
這便是權重初始化的核心概念:即通過控制權重的方差,讓信號方差保持恆定。 既避免了梯度爆炸,又避免了梯度消失。
在此思想上,便發展出了以下幾種適應不同激活函數的初始化,涉及具體實驗和文獻,就不再展開了:
| 初始化方法 | 核心思想 | 適用激活函數 | 公式 | 舉例説明 |
|---|---|---|---|---|
| Xavier (Glorot) | 讓輸入輸出方差一致 | Sigmoid / Tanh | \(Var(W)=\frac{1}{n_{in}+n_{out}}\) | 若一層輸入神經元 100 個、輸出 50 個:
\(Var(W)=1/(150)=0.0067\) |
| He (Kaiming) | 針對 ReLU 激活的特性調整 | ReLU / Leaky ReLU | \(Var(W)=\frac{2}{n_{in}}\) | 輸入 100 個神經元 → \(Var(W)=0.02\) |
總結一下,把權重初始化為合適的方差,相當於在網絡剛開始訓練時把“信號音量”調到合適的檔位,這能讓信號在層間既不被放大成噪音(爆炸),也不被削弱成耳語(消失)。不同激活函數會改變信號統計特性,所以需要不同的初始化。
2.梯度檢驗(Gradient Checking)
梯度檢驗的目標是驗證反向傳播計算的梯度是否正確。
這在早期手寫反向傳播時代是非常重要的調試工具。
梯度檢驗的核心思想是:用數值方法逼近梯度,再與反向傳播計算的梯度對比,檢查實現是否正確,我們用實例來更好的説明這個過程。
2.1計算數值梯度
首先,假設損失函數為:\(J(\theta) = \theta^2\)
當前參數:\(\theta = 3\)
然後,用有限差分法近似梯度:
計算:
現在我們就得到了數值梯度,這是我們用有限差分計算得到的實際數值。
2.2 計算理論梯度
現在,對損失函數求導代入:
現在我們就得到了理論梯度,這是我們通過求導得到的理論答案。
2.3 進行梯度檢驗
梯度檢驗的公式如下:
結果為 \(0\),説明反向傳播梯度實現正確,但實際上的數值不會這麼簡單。
若我們的反向傳播錯誤(例如少乘了一項),數值梯度與反向傳播梯度之間的差異就會很明顯,從而發現問題。
對梯度檢驗的結果判別如下:
| error 量級 | 含義 |
|---|---|
| \(error < 10^{-7}\) | 極小誤差,反向傳播實現完全正確 |
| \(10^{-7} \le error < 10^{-4}\) | 誤差較小,可接受,可能存在微小數值舍入差異 |
| \(10^{-4} \le error < 10^{-2}\) | 誤差明顯,反向傳播可能有小錯誤,需要檢查 |
| \(error \ge 10^{-2}\) | 誤差很大,反向傳播實現錯誤明顯 |
這便是早期梯度檢驗的主要過程,但在現在已經很少使用了。
2.4 實際運用中要注意的點
在實際使用梯度檢驗時,需要注意以下幾點:
- 梯度檢驗不用於訓練
- 梯度檢驗的目的是驗證反向傳播實現是否正確,並不是訓練算法本身。
- 它通常只在模型開發階段使用,一旦確認實現正確,就可以關閉,以免浪費計算資源。
- 梯度檢驗和 Dropout/正則化一般不一起使用
- Dropout 操作會引入隨機性,會導致數值梯度和反向傳播梯度不完全一致。
- 為了保證梯度檢驗結果準確,通常需要在 關閉 Dropout 的訓練模式 下進行。
3.”人話版“總結
| 概念 | 原理 | 作用 | 比喻 |
|---|---|---|---|
| 梯度消失 | 信號在多層網絡中逐層縮小,導致反向傳播梯度幾乎為 0 | 網絡學習極慢,權重幾乎不更新 | 傳話遊戲越傳越小聲,最後聽不見 |
| 梯度爆炸 | 信號在多層網絡中逐層放大,導致反向傳播梯度非常大 | 網絡訓練不穩定,loss 發散或 NaN | 傳話遊戲越傳越大聲,最後系統崩潰 |
| 權重初始化 | 給權重一個合適方差,使每層輸出方差 ≈ 輸入方差 | 避免梯度消失或爆炸,讓信號穩定傳播 | 調音器把每層信號音量調到合適檔位,既不吵也不小聲 |
| 梯度檢驗 | 用數值方法近似梯度,與反向傳播梯度比對 | 驗證反向傳播是否正確 | 對照答案檢查作業,發現漏算或寫錯的地方 |