在各類XAML UI框架中,Grid 是一種非常靈活且常用的佈局控件,它可以創建複雜的用户界面佈局。Grid 允許開發者通過定義行和列來組織界面元素,每個元素可以精確地放置在網格的特定區域內
本文以 Avalonia 框架為例,講解 Grid 控件的工作原理
事實上,UWP、WinUI 3 和 Avalonia 等XAML框架中
Grid控件的源碼全都源自於 WPF 中的實現,以至於絕大部分代碼乃至註釋都是相同的因此,本文中你能瞭解到的機制也可應用於其他 XAML UI 框架
Measure 階段
快速路徑:當僅僅存在一個行/列(或未定義行列)時,將子元素中最大的寬和高設置為為
Grid的大小即可。gridDesiredSize = new Size( Math.Max(gridDesiredSize.Width, child.DesiredSize.Width), Math.Max(gridDesiredSize.Height, child.DesiredSize.Height));
在一般情況下,我們定義了兩個及以上以上的行/列,就需要一套特定的算法進行計算
我們知道,Grid的行/列定義有Auto、Star、Pixel三類
簡化後的定義如下:
public class Definition
{
public double MinSize { get; set; }// 對應MinHeight(MinWidth),以Pixel為單位
public double MaxSize { get; set; }// 對應MaxHeight(MaxWidth),以Pixel為單位
public GridLength Size { get; set; }// 對應Height(Width),對應不同單位下的值
double MeasureSize { get; set; }// 測量階段的結果
double FinalSize { get; set; }// 排列階段的結果
double FinalOffset { get; set; }// 最終偏移量
}
此處將
Width/Height更改為Size,不再區分行列源代碼中為了性能,上面的一些屬性(如
FinalSize、MaxSize)使用的是同一個字段,為便於理解,這裏將他們拆分開來單獨列出。具體代碼可以自行前往Avalonia存儲庫查看
在測量 (Measure) 的過程中,Grid 遵循"可確定大小優先"的原則。因此,他們將要渲染的元素分為四組來決定測量順序
Px |
Auto |
Star |
|
|---|---|---|---|
Px |
1 | 1 | 3 |
Auto |
1 | 1 | 3 |
Star |
4 | 2 | 4 |
通常情況下,測量的順序如下:
根據
Group2、Group3元素的存在情況,測量組和解析Star項的順序會有所不同,但Group1和Group4的測量順序始終不變具體流程將在後面介紹
我們先依次介紹 Measure 過程中使用的主要算法
ValidateDefinitionsStructure、ValidateDefinitionsLayout:初始化行/列定義
分組前,Grid 會先初始化行/列定義的結構:如果只有行定義,Grid 會自動添加一個 Width = * 的列定義;同理,如果只有列定義,會自動添加一個行定義
同時,如果傳入了無限的長或寬,其對應的所有 Star 定義都會被視作 Auto 項
ValidateCells:分組,預處理所有子元素
分組過程中,Grid 中的每個元素都將被視作一個 Cell,他們根據所在行/列的類型被分配到不同組中,以便稍後進行進一步的計算
所有 Cell 以鏈表的形式被緩存,每個 CellGroup 存儲的是當前組的頭節點,在後續測量中使用 Cell.Next 進行遍歷
MeasureCellsGroup:測量組
Group = 1:項的類型為 Px/Auto
測量每個元素的機制如下:
-
Px項:def.Size作為元素Measure邊界 -
Auto項:傳入無限尺寸作為元素Measure邊界同時,當某個元素測量完成時,還會根據元素的高度更新元素所在項的最小大小
項最小尺寸的初始值與最大尺寸由用户設定,如
RowDefinition.Min/MaxHeightdef.MinSize = Math.Clamp(child.DesiredSize, def.MinSize, def.MaxSize)若元素的
RowSpan > 1(可能跨項),則不更新項最小值,並且在其他元素均測量完畢後,確保這些跨項元素尺寸在其所在所有項尺寸的最小值/最大值之間
Group ≠ 1:元素在某個 Star 類型的項中
根據順序,此時已完成目標組
Star項的大小解析,因此definitions.MeasureSize是有值的
使用 GetMeasureSizeForRange 方法,遍歷元素跨越的所有項,將這些項的最小值(Auto 項)或測量值(Star 項)相加,得到元素測量時的邊界
private static double GetMeasureSizeForRange(
IReadOnlyList<DefinitionBase> definitions,
int start/*起始項位置*/,
int count/*跨越項數(RowSpan)*/,
double spacing)
{
double measureSize = -spacing;
int i = start + count - 1;
do
{
measureSize +=
spacing + // 跨行元素可忽視所跨項之間的spacing
(definitions[i].SizeType == LayoutTimeSizeType.Auto ?
definitions[i].MinSize :
definitions[i].MeasureSize);
} while (--i >= start);
return measureSize;
}
同理,每個元素測量完成時也會更新其所在項的最小值,也會在所有元素測量完成後確保跨項元素尺寸在正確範圍內
ResolveStar:統一解析Star項,分配權重
Group1 測量完畢後,我們已經得到了所有固定元素的尺寸,現在以以下流程計算各 Star 項的尺寸:
-
預處理權重
遍歷
definitions,統計Star項的數量並得到最大權重maxStar,同時將所有Star項的MeasureSize設置為 1.0,表示尚未在後續階段解析。引入
scale值用於後續縮放,防止浮點溢出:- 若存在 Infinity 權重,設置
scale = -1.0 - 若不存在 Infinity 權重但權重和可能溢出(
starCount * maxStar > Double.Max),將scale設置為 2 的負次冪
- 若存在 Infinity 權重,設置
-
計算可用空間,預處理約束
再次遍歷
definitions,計算所有非Star項所佔用的空間takenSize對於
Star項,計算縮放後的權重值starWeight = star * scale,並累計到totalStarWeight- 若 scale < 0(存在Infinity權重),將 Infinity 項映射為 1,其餘映射為 0
如果項存在最小約束(
MinSize > 0,由用户設置),將該項加入"最小約束列表",並暫存比率def.minRatio = starWeight / def.MinSize同理,若存在最大約束(
MaxSize ≠ Infinity),將該項加入"最大約束列表",暫存def.maxRatio = starWeight / def.MaxSize為提升性能,實際實現中"最小約束列表"和"最大約束列表"存儲在同一列表
definitionIndices中,分別為前後兩個部分 -
迭代解析約束項
來看一個例子:
<!--C1--><ColumnDefinition Width="*" MinWidth="120"/> <!--C2--><ColumnDefinition Width="2*"/> <!--C3--><ColumnDefinition Width="3*" MaxWidth="150"/>假設可用尺寸
S=400,這時候我們可以發現:如果要滿足定義中的Min/MaxWidth約束,是無法實現 1 : 2 : 3 的比例的。因此,我們需要將與比例差距最大的項"鎖定"為Min/MaxWidth但我們又希望鎖定後的比例儘可能接近定義的比例,因此
Grid使用了以下算法:flowchart TD A["階段3:處理約束項"] B["按照 最小比率、最大比率 排序約束列表"] C{"有剩餘空間且存在未處理的約束項?"} D["計算當前比例"] E{"是否違反某個約束?"} F["選擇偏差最大的約束"] G["將該項尺寸鎖定為此約束值"] H["更新剩餘權重與剩餘空間"] I["結束"] A --> B --> C C -- "是" --> D D --> E C -- "否" --> I E -- "是" --> F F --> G --> H E -- "否" --> I H --> C先對最小約束列表按照比率降序,最大約束列表按照比率升序排序
初始
remainingAvailableSize=S=400,remainingStarWeight=W=6下面按照每次鎖定"差異最大"的一個
definition來迭代解析約束項:第一次迭代:
-
從最小/最大約束列表中分別選出
C1.minRatio== 1/120 == 0.008333 ,C3.maxRatio== 3/150 == 0.02 -
計算比例
proportion = remainingStarWeight / remainingAvailableSize= 6/400 = 0.015 -
判定是否違反比例:
- 違反最小約束:
minRatio < proportion=> 0.008333 < 0.015(成立) - 違反最大約束:
maxRatio > proportion=> 0.02 > 0.015(成立)
如果認為"比例"不好理解,可以從反面考慮:
假設步驟 2 中
def.MinSize / starWeight代表每顆星的最小大小minStarSize,def.MaxSize / starWeight代表每顆星允許的最大大小maxStarSize那麼
remainingAvailableSize / remainingStarWeight代表當前每顆星的大小currentStarSize必須滿足
minStarSize ≤ currentStarSize ≤ maxStarSize,否則就需要選擇偏離最大的項進行鎖定 - 違反最小約束:
-
二者都需要鎖定,選擇偏離更大的一項:
-
對最小約束的偏離:
proportion / minRatio= 0.015 / 0.008333 ≈ 1.8 -
對最大約束的偏離:
maxRatio / proportion= 0.02 / 0.015 ≈ 1.333 -
1.8 > 1.333 => 優先鎖定
C1尺寸為C1.MinSize
-
-
執行鎖定:
-
設置
C1尺寸為約束最小值:resolvedSize = C1.MinSize = 120 -
更新可用空間和剩餘權重:
remainingAvailableSize = 400 - resolvedSize = 400-120 = 280remainingStarWeight = 6 - C3.starWeight = 6 - 1 = 5
-
第二次迭代:
-
maxRatio= 0.02(仍為C3) -
proportion= 5/280 ≈ 0.017857 -
僅違反最大約束:0.02 > 0.017857 =>
C3尺寸鎖定為C3.MaxSize -
執行鎖定:
- 設置
C3尺寸為約束最大值:resolvedSize = C3.MaxSize= 150 remainingAvailableSize= 280 -150 = 130;remainingStarWeight= 5 - 3 = 2
- 設置
最小/最大約束列表均為空 => 退出。
-
-
檢測異常場景並重復執行 2、3
完成步驟 3 後,可能會有以下異常場景:
-
remainingAvailableSize > 0且Star項全部處理完畢:所有Star項都被其最大約束鎖定,但所有最大約束之和仍小於邊界遍歷所有項,解鎖存在最小約束的項,重新執行步驟 2、3 為其分配空間
-
remainingAvailableSize < 0:某些項被最小約束鎖定,但所有最小約束之和超過了邊界同理,解鎖存在最大約束的項,重新執行 2、3
-
-
前綴和算法分配剩餘空間
相比
權重/權重總和*剩餘空間,此算法可以避免浮點數計算帶來的精度丟失可以用一個例子説明此算法:
假設權重分別為
[1, 2, 3],剩餘空間為 6計算權重前綴和
[1, 3, 6]現在以權重從大到小的順序開始分配
- 分配
6*(3/6) = 3,剩餘空間 6-3=3 - 分配
3*(2/3) = 2,剩餘空間 3-2=1 - 分配
1*(1/1) = 1,剩餘空間 1-1=0,完成
簡化後的算法如下(此處默認所有項的類型為
Star):Array.Sort(definitions); // 計算前綴和 totalStarWeight = 0.0; for (int i = 0; i < definitions.Length; ++i) { DefinitionBase def = definitions[i]; totalStarWeight += def.MeasureSize;// MeasureSize在此處代表Star數量 def.SizeCache = totalStarWeight;// SizeCache用於緩存前綴和結果 } // 從後向前遍歷 for (int i = definitions.Length - 1; i >= 0; --i) { DefinitionBase def = definitions[i]; double resolvedSize = (availableSize - takenSize) * (def.MeasureSize / def.SizeCache); def.MeasureSize = resolvedSize; takenSize += resolvedSize; } - 分配
現在,你應該對測量中使用的算法有了大概瞭解。但測量順序具體是怎麼樣的呢?以及,為什麼要遵守這樣的測量順序?
我們再看一下之前的分組表:
Px |
Auto |
Star |
|
|---|---|---|---|
Px |
1 | 1 | 3 |
Auto |
1 | 1 | 3 [A] |
Star |
4 | 2 [B] | 4 |
重點看加粗的部分:以 A部分 (在 Group3 中)為例,在測量這部分的元素前,必須得到 Auto 列的大小。因此,測量 Group3 前必須完成對 Group1 和 Group2的測量
同樣,B 部分在測量之前也必須得到 Auto 行的大小,在測量 Group2 前必須完成對 Group1 和 Group3 的測量
AB 部分的共同特性就是同時存在於 Auto 和 Star 項中,我們可以得出以下結論:
- A 部分中存在元素:測量
Group1、Group2後才能測量Group3 - B 部分中存在元素:測量
Group1、Group3後才能測量Group2
如果 A、B 部分都存在元素呢?比如下面的情況:
| column width="Auto" | column width="*" | |
|---|---|---|
| row height="Auto" | cell 1 2 [A] | |
| row height="*" | cell 2 1 [B] |
由於 cell 2 1 的寬度決定了 Auto 列的寬度,進而間接決定 cell 1 2 所在列的寬度,需要先計算 cell 2 1。然而,由於 cell 1 2 的高度決定了 Auto 行的高度,同理, cell 2 1 也理應先被計算—— Auto 與 Star 的行列相互影響,這就是 Grid 行列解析中的循環依賴問題。
綜上所述,Grid 共有三種不同的測量順序,流程圖如下:
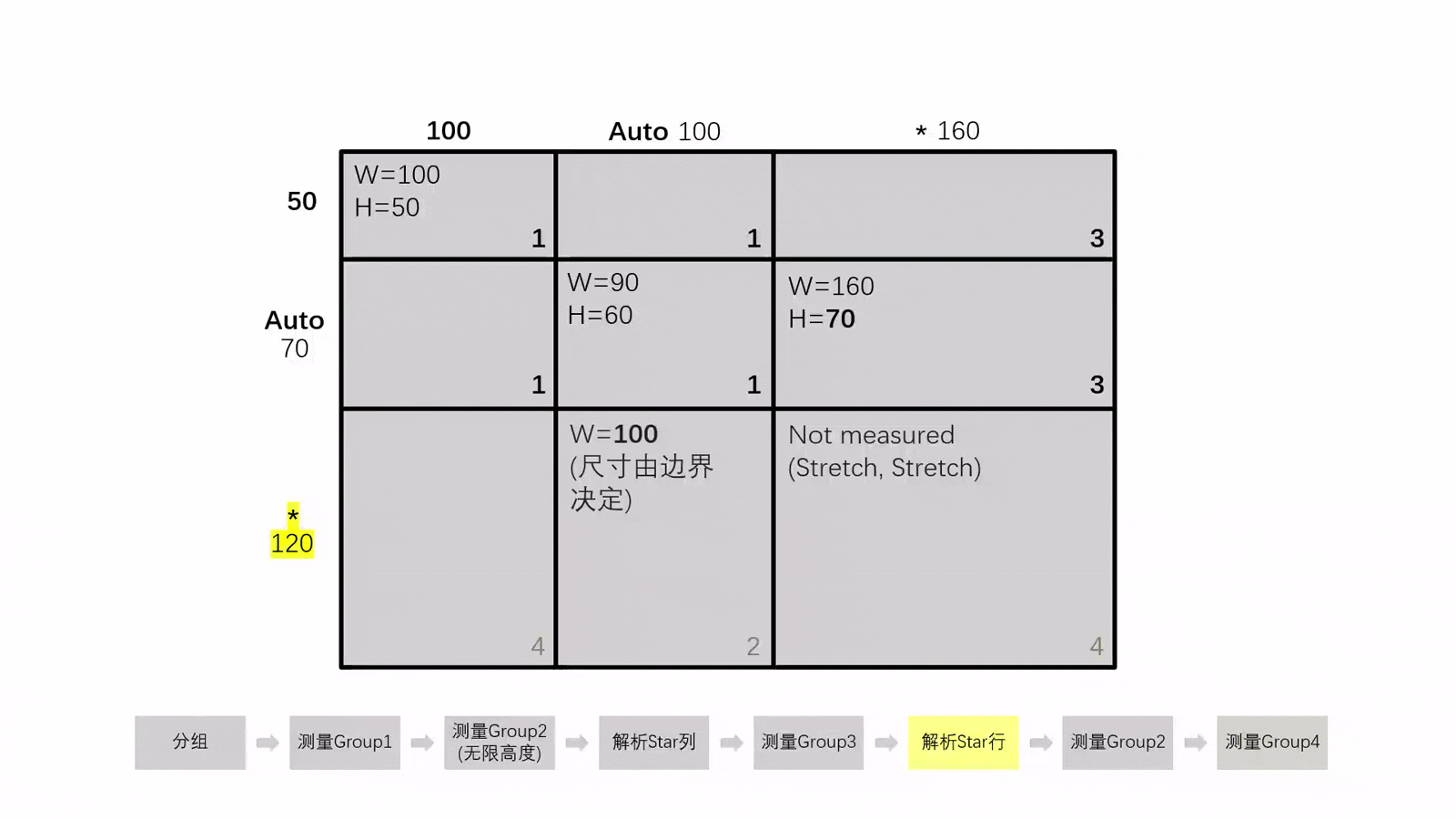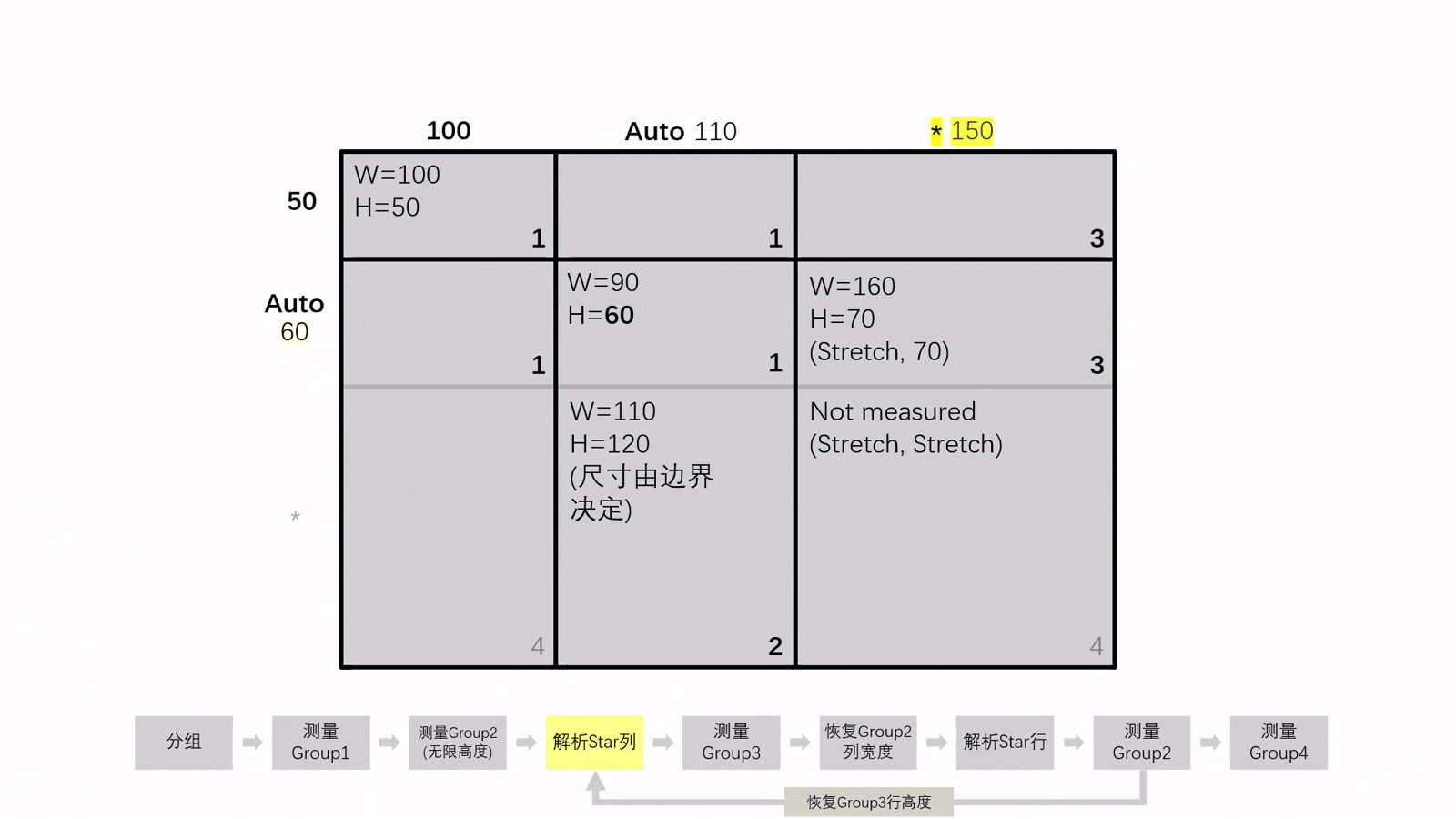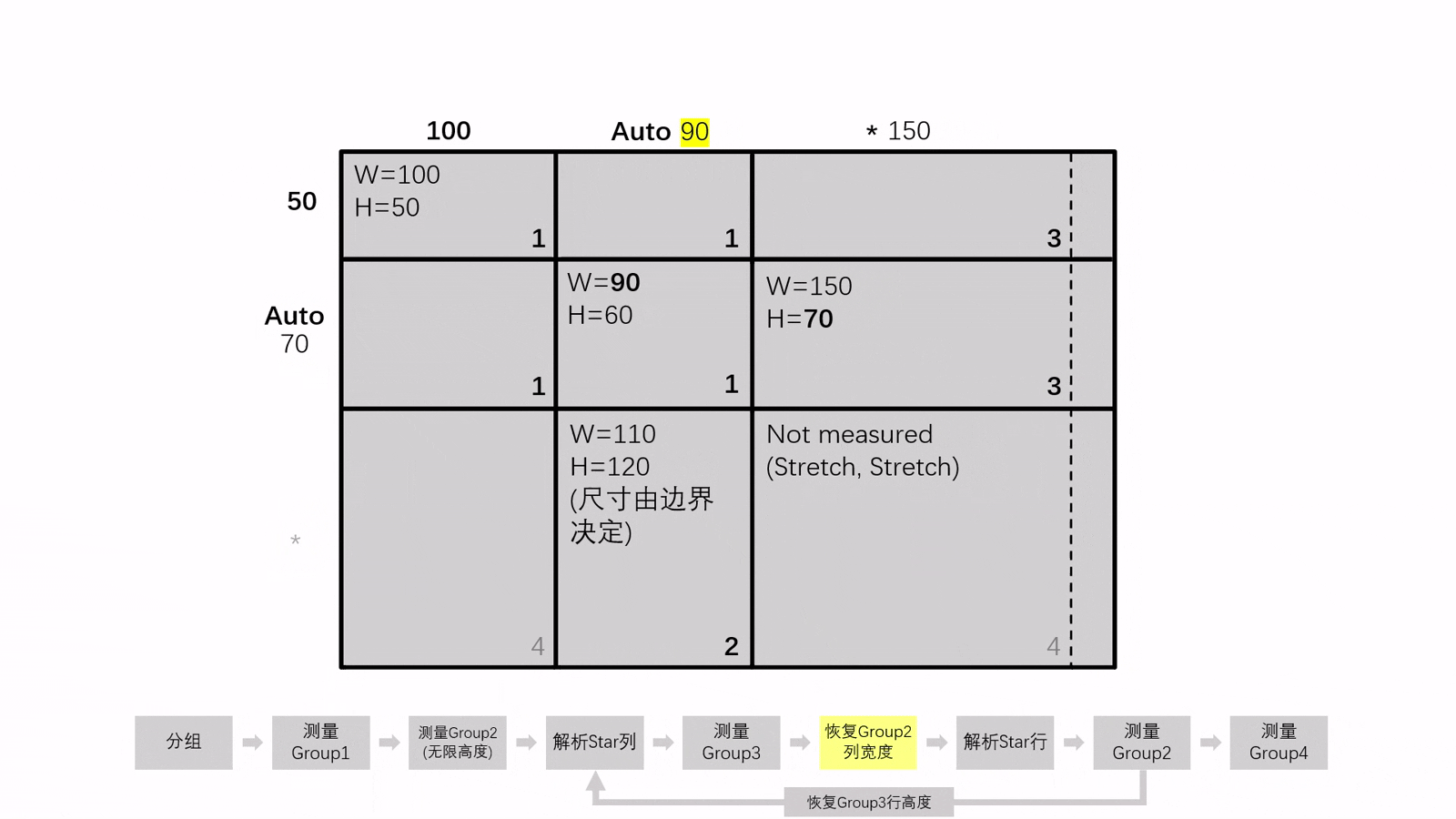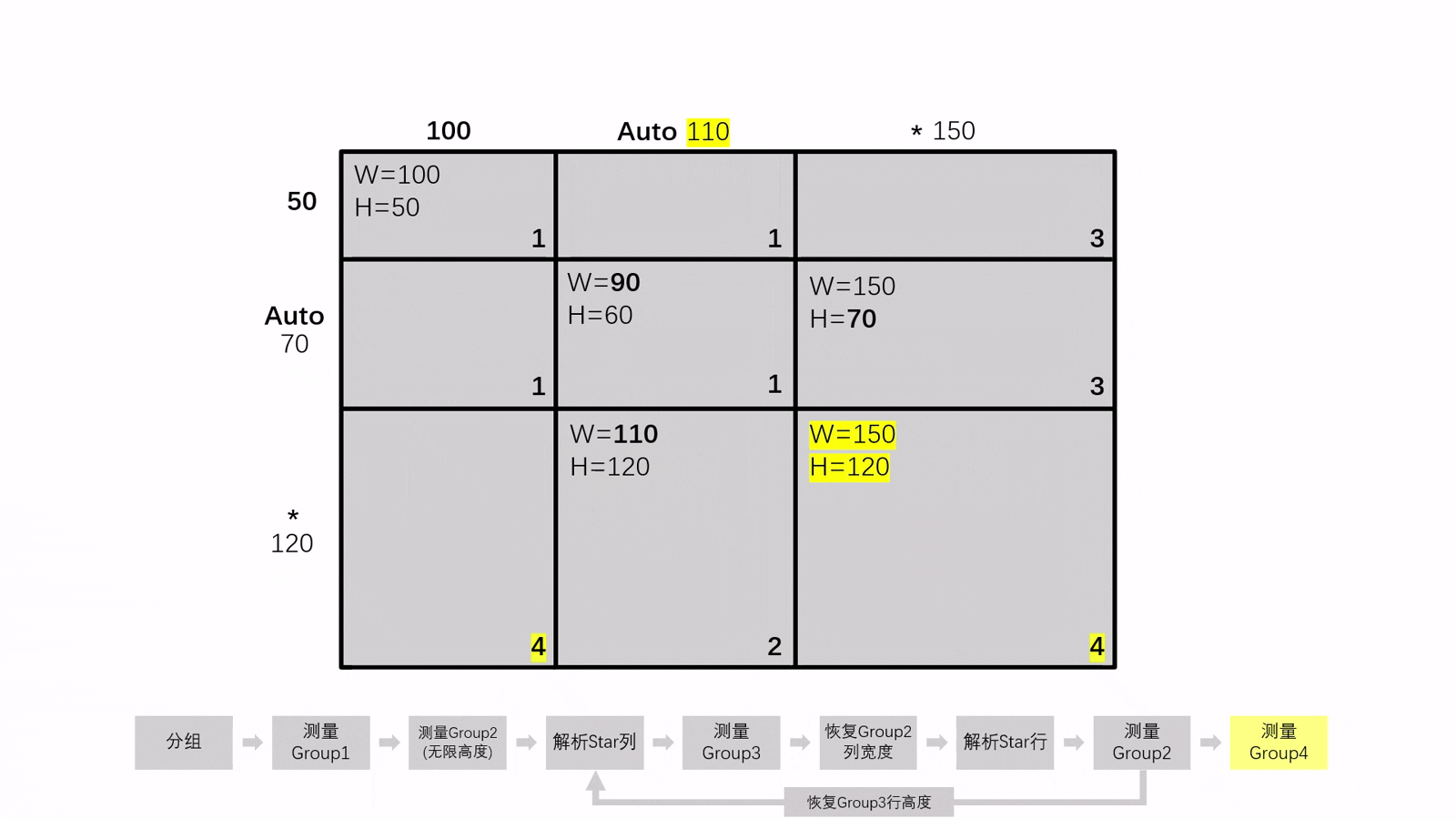
循環依賴的處理
對於產生了循環依賴的佈局,我們無法直接測量 AB 組的大小。因此,我們需要先在測量 Group2(也就是 B 組) 時使用無限高度以先得到其寬度,再解析 Star 列
Star列被解析完畢後,就可以測量 Group3 中的元素了,此時再解析Star行即可重新以正確的行高測量 Group2
更為極端的情況
如果 Group2 中的元素再使用不同高度測量時得到的寬度不同(例如,縱向排列的 WrapPanel ),這代表第一次使用無限高度測量 Group2 後解析得到Star列的寬度是錯誤的!這時候我們需要返回並重新對 Group3 進行測量...
在重新測量的過程中,我們還要將 Auto 項的尺寸恢復到測量 Group1 後的狀態,來儘可能保證測量 Group2 時的參數相等
此流程會一直循環,直到兩次Group2寬度的測量結果相同或循環次數 ≥5
Arrange 階段
由於行列大小計算已經在 Measure 階段完成,Arrange 階段只需要計算每個行列的最終位置並處理一些特殊設置即可。
重新解析 Star 項
由於 Measure 階段提供的約束可能與 Arrange 階段提供的空間不一致,我們需要使用與 ResolveStar 相同的方式再次解析一遍 Star 項
至於為何兩個階段提供的空間可能不一致,就涉及到 Measure/Arrange 機制了,具體可參閲 佈局 - WPF | Microsoft Learn
Spacing 處理
在 Measure 階段前,我們在原邊界大小的基礎上減去所有間距之和後再進行測量,對 spacing 的單獨處理僅限於跨行元素(見GetMeasureSizeForRange)。
因此,在處理元素最終的偏移量 FinalOffset 時,我們需要在每次迭代都加上對應的 spacing
for (int i = 0; i < definitions.Count; ++i)
{
definitions[(i + 1) % definitions.Count].FinalOffset = definitions[i].FinalOffset + definitions[i].FinalSize + spacing;
}
佈局舍入 (LayoutRounding)
為了避免影響前面的測量進程,佈局舍入在 Arrange 的最後階段執行
- 遍歷所有項,將其尺寸根據當前 DPI 四捨五入,並把舍入後大小 - 原始大小寫入
RoundingErrors - 計算舍入後大小
roundedTakenSize與舍入前大小finalSize的差值。若不相等,就需要進一步調節各項以分配餘額或去除溢出 - 將所有項根據
RoundingErrors排序,在差值最大的項上增加或減少像素(以dpiIncrement = 1 / dpi為單位)進行調節,同時確保不低於MinSize
順帶一提,代碼中用了一段很長的註釋來説明當前的佈局舍入算法是存在問題且無法解決的:
(由 Gemini 3 Pro 翻譯) // 理論和歷史説明。當前的問題——即在帶有星號權重(*-weights)、 // 最小和最大約束以及佈局舍入的情況下向列(或行)分配空間——由來已久。 // 特別是那個著名的特例:50列,最小值為1,可用空間為435—— // 這正是根據人口比例向50個州分配美國眾議院席位的問題。 // 關於這一問題的算法和論文無數,最早可追溯到1700年代,包括這本書: // Balinski, M. 和 H. Young 所著的《Fair Representation》(公平代表),耶魯大學出版社,紐黑文,1982年。 // // 所有這些研究得出的一個驚人結果是:*任何*算法都難免會遭受一個或多個 // 不良特性的困擾,例如“人口悖論”或“阿拉巴馬悖論”。 // 在這種情況下(套用我們的術語來説),增加一個像素的可用空間實際上 // 可能會減少分配給特定列的空間,或者增加某列的權重反而可能會減少其分配量。 // 這一點值得了解,以防有人抱怨這種行為;這與其説是一個 Bug, // 不如説是問題本身固有的特性。引用上面提到的書或數百篇參考文獻之一, // 然後將其標記為“不予修復”(WontFix)。 // // 幸運的是,我們的場景通常只有少量的列(約10列或更少), // 每列分配大量的像素(約50個或更多),人們甚至注意不到 // 理論上不可避免的那種1像素的偏差,或者即使注意到了也不在乎。 // 至少他們不應該在乎——沒人應該使用 WPF 網格佈局的結果來做 // 定量決策;它的工作是產生合理的顯示效果,而不是分配國會席位。 // // 我們的算法比當前用於國會席位分配的算法(“亨廷頓-希爾”算法) // 更容易出現悖論,但它的運行速度更快: // 複雜度為 O(N log N) vs. O(S * N),其中 N=定義的數量,S=可用像素的數量。 // 並且如上所述,它在實踐中產生了足夠好的結果。 // // 重申一點:所有這些僅在啓用佈局舍入時適用。 // 當允許小數尺寸時,該算法在受限於最小/最大約束和 // 浮點計算精度的情況下表現儘可能良好。 // (但是,最終的顯示結果會受到抗鋸齒問題的影響。天下沒有免費的午餐 [TANSTAAFL]。)
總結
通過了解 Grid 的有關算法,我們可以得到一些結論
-
Grid的工作流程相當複雜。儘管存在快速分支,仍然會進行很多不必要的判斷與計算因此,對於不需要定義行列的簡單多元素佈局需求,我們應儘量使用其他控件代替,如 Avalonia 中的
Panel控件 -
儘量不要將非固定大小元素(如
WrapPanel)同時放在Star和Auto項中這可能導致循環依賴並多次對元素進行測量。而對於
WrapPanel這類列表控件,測量的開支是非常大的! -
Grid仍然存在一些未定義的行為,參見 WPF/UWP 的 Grid 佈局竟然有 Bug,還不止一個!瞭解 Grid 中那些未定義的佈局規則 - walterlv例如這篇文章中提到的第一個問題,就是在
ValidateDefinitionsLayout的過程中Star項被視作Auto項導致的,但官方文檔並沒有進行明確的記載如果有時間,我可能會再寫一篇文章來單獨説明這些未定義佈局規則的原因
-
能夠考慮到如此多的極端情況,微軟的 WPF 工程師確實有實力...——當然對於一個廣泛使用的 UI 框架,這些情況也是有必要考慮在內的