1.數據類型

c語言自帶的一些數據類型

char      //字符型       1byte
short     //短整型       2byte
int       //整型         4byte
long      //長整型       4 or 8byte
long long //更長的整型    8byte
float     //單精度浮點數  4byte
double    //雙精度浮點數  8byte

long在不同環境中字節大小不同（比如VS中是4byte）

1.1類型的分類

整型

char
	unsigned char
	signed char
short
	unsigned short
	signed short
int
	unsigned int
	signed int
long
	unsigned long
	signed long
long long
	unsigned long long
	signed long long

字符在內存中存放的是ASCII碼值，所以也算作整型
在寫代碼的時候，不説明類型是否有符號，默認為signed，char類型除外，它的默認取決於編譯器
如果在定義時，定義的為signed 整型，那麼其在內存中存儲的n位二進制的最高位為符號位，符號位為1表示負數，符號位為0表示正數，對於無符號數，最高位也是計數位，所以計數範圍更大
浮點型

float
double
long double

構造類型（自定義類型）

數組類型
結構體類型 struct
枚舉類型  enum
聯合類型  union

指針類型

int* p1
void* p2
float* p3

空類型

void

常見於函數傳參，函數返回值類型，指針類型

2.整型在內存中的存儲

整型的取值範圍在頭文件<limits.h>中定義

整數的二進制表示形式有3種：
原碼：整數的二進制形式（多少位由類型所佔多少字節空間決定）
反碼：原碼符號位不變，其他位按位取反
補碼：反碼加一
正整數的原碼，反碼，補碼相同，都等於原碼
負整數的三種形式才需要按上述方式計算

int a = -5
//原碼：10000000 00000000 00000000 00000101
	0x80 00 00 05
//反碼：11111111 11111111 11111111 11111010
	oxff ff ff fa
//補碼：11111111 11111111 11111111 11111011
	0xff ff ff fb
要注意符號位不變

內存中存放整數時存放的其二進制補碼
事實上，原碼和補碼互換的運算邏輯是一致的，補碼等於原碼取反加一，而原碼也等於反碼取反加一（可見如今的計算機能有今天，要歷經多少天才的發明）

2.2大小端

我們在編譯器中看內存窗口時，會看到數據在內存按地址的存放順序，那數據在內存中存放的邏輯是怎樣的呢？
有下面兩種存放方式
字節序：字節數據在內存中的存放順序
大端字節序存儲：指將高位字節存儲在內存的低地址，而低位字節存儲在高地址
小端字節序存儲：指將低位字節存儲在內存的低地址，而高位字節存儲在高地址

2.3整型提升

整型在存放和計算過程中還會涉及到整型提升和截斷，可以看我另一篇博客

3. 浮點數在內存中的存儲

浮點數的表示範圍在頭文件<float.h>中定義

如果想明白這個問題，我們必須清楚小數的概念

3.1二進制小數

所有的實數按照能否用分數表示分為兩大類
1.有理數（整數，分數）
2.無理數（不能表示成任何分數形式的數）
而小數，是實數的一種位值制的書寫形式，而不同進制決定了這種書寫的具體規則，本質上是用整數部分+小數部分的統一格式表示
你可能會問，説這麼複雜，和標題有什麼關係？
我們來分析一下小數的書寫規則
在十進制中（基數為10）
小數點的左邊分別為10⁰（個位） ,10¹（十位）,10²（百位）....小數點右邊為10^-1（十分位）,10^-2（百分位）,10^-3（千分位）....
小數點每左移一位，數值10^-1
在二進制中（基數為2）
小數點的左邊分別為2⁰（個位）,2¹（二位）,2²（四位）...,小數點右邊為2^-1（1/2）,2^-2（1/4）,2^-3（1/8）....
小數點每左移一位，數值2^-1
在16進制中（基數為16）
小數點的左邊分別為16⁰（個位）,16¹（16位）,16²（256位）...,小數點右邊為16^-1（1/16）,16^-2（1/256）,16^-3（1/4096）....
小數點每左移一位，數值*16^-1
。。。。。。
任何一種進制都有其自己的整數部分和小數部分的表示形式，無論是有理數還是無理數，而分數就是分數，不受進制的影響

想必你現在已經明白小數的定義了，還理解了二進制小數部分的運算規則

3.2不同進制間的小數表示

我們知道，不同進制之間的整數部分可以相互轉換，小數部分也是可以的
但對於小數部分存在着轉換的限制
比如十進制小數轉化為二進制
一個分數能寫成有限小數，在不同進制中條件是不同的
在十進制，分數能寫成有限小數，只有一個條件，把分母化成最簡形式後，分母的質因數（既是質數，又是某數的因數）只能是2或5
1/2 = 0.5
1/5 = 0.2
1/10 = 0.1
但1/3，1/7不能化為十進制的有限小數
在二進制中，分數能寫成有限小數，最簡分母的質因數只有2
1/2 = 0.1
1/4 = 0.01
1/8 = 0.001
你會發現1/10（質因數包含2和5），在二進制中無法精準表示，這也解釋了為什麼有些十進制小數無法用二進制來精確表示（0.1就不行）這是因為二進制小數的分母的質因數只有2，沒有5，所以他不能表示十進制中最簡分母質因數包含2和5的小數
其他進制也是同理，當然不同進制間的小數轉換，這是個複雜的問題，甚至包含有限小數轉無限小數，這裏只探討十進制和二進制，這也是主題要用到的

3.3二進制小數的別樣表示

我們給出一個十進制浮點數10.5
轉換為二進制是1010.1
它可以寫成1.0101*2³（類似於科學計數法就比如123.456可以寫成1.23456 *10²）
還可以寫成（-1）⁰ *1.0101 *2³
我們發現，對於任意的一個二進制浮點數（不考慮不能寫成二進制小數的十進制小數）都可以寫成
v=(-1)^S *M *2^E
這裏v代表浮點數，S代表符號位，M代表有效數字，E代表指數位
當S為1時表示負數，S為0時表示正數
E控制小數點的位置
M是存儲的有效部分，整數部分不存儲，讀取時默認為1，只存小數部分（二進制使用這種計數法，整數位只可能是1）
既然任何一種二進制浮點數都可以表示成這種形式，那麼浮點數在內存中的存儲只需存儲3個變量S,E,M

3.4浮點數的存儲

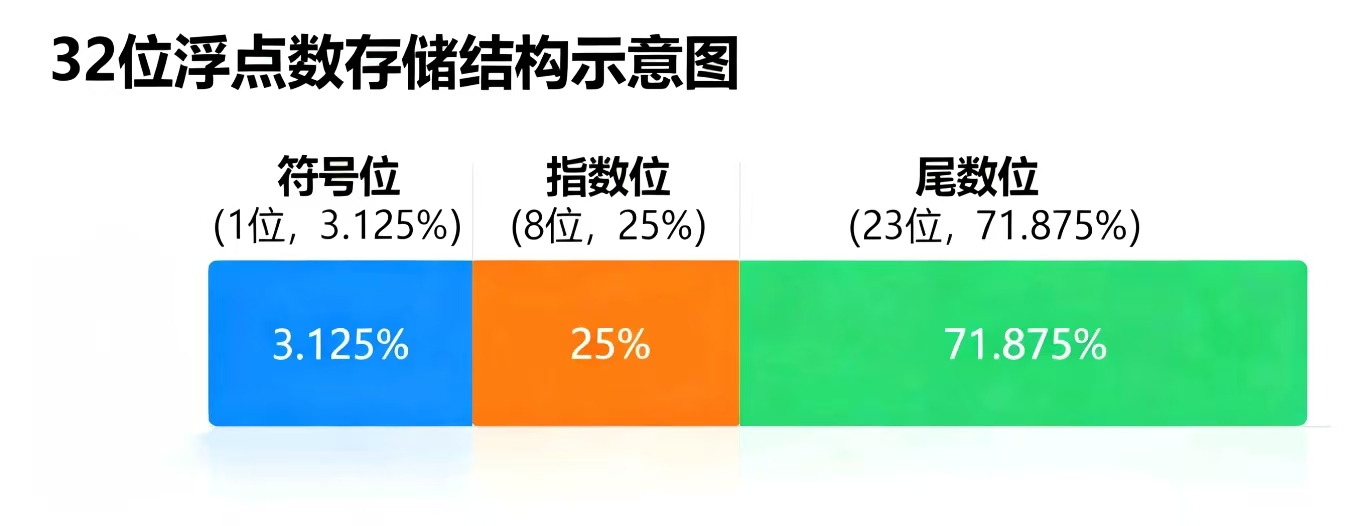
對於32位的浮點數IEEE規定
S佔1bit（最高位）
E佔8bit（中間）
M佔23bit（最後）

對於64位的浮點數來説
S佔1bit
E佔11bit
M佔52bit

對於M,IEEE754規定，在計算機保存M時，默認這個數的第一位總是1，因此捨去，只保留後面的小數部分，當讀取的時候，再把1加上
對於E，首先其存儲時是unsigned int，但實際情況中E有可能是負數，所以IEEE754規定，在存儲E的時候要加上一個偏移量，把計算的結果存進去，單精度的是127，雙精度的是1023
比如我要存-1進去，實際存放的E是126
存儲的位數不夠32位或64，在後面補0
5.5f
101.1
（-1）⁰ *1.011 *2²
s = 0,M =1.011 e=2 (129)
32位 0 10000001 011 00000000000000000000
0x40 b0 00 00（顯示成16進制）
這就是5.5在float類型變量中的存儲