• 論文原文 ：https://arxiv.org/abs/2505.23049
• 項目地址 ：https://github.com/Axel-gu/DenoiseRotator
• 視頻解讀（B站） ：https://www.bilibili.com/video/BV1XDUYBTEjr

在大語言模型（LLM）快速發展的今天，龐大的參數規模帶來高昂的推理存儲成本和回覆時延，已成為實際應用中的關鍵挑戰。特別是在面向人機對話的應用場景，模型推理效率直接影響到對話體驗。在推理優化方法中，參數剪枝作為一項經典的模型壓縮技術，旨在通過剔除模型中"不重要"的權重來實現參數量的顯著降低與計算效率的提升。然而，傳統的"剪枝-微調"範式或直接的後訓練剪枝方法，往往帶來明顯的模型性能損失，特別是在硬件友好的半結構化稀疏（如2:4稀疏）場景下，該問題尤為突出。這使得應用中的模型效果和推理效率，呈現一個"魚和熊掌"的兩難局面。

{{{width="auto" height="auto"}}}

面對這項挑戰，美團LongCat Interaction團隊聯合上海交通大學聽覺認知與計算聲學實驗室，以及香港科技大學的研究者，共同完成了大模型剪枝方法的創新研究，提出了名為DenoiseRotator的新技術。通過首先對參數矩陣進行變換，"濃縮"對結果有影響力的參數，再對重要性最低的參數進行剪枝，實現了大模型剪枝的新範式。DenoiseRotator能夠與現有的剪枝算法快速集成，有效緩解模型壓縮帶來的性能損失。這一研究成果已在2025年的NeurIPS會議上發表。

01 動機：傳統剪枝的侷限性------密集訓練與稀疏推理的隱式衝突

傳統後訓練剪枝的一般流程可概括為：對一個已訓練好的稠密模型 ，基於某種啓發式準則（如權重幅值或Wanda、SparseGPT等算法）為每個參數賦予"重要性分數"，隨後根據預設的稀疏度閾值，移除分數較低的一部分權重。 儘管流程清晰，該方法存在一個本質侷限：其整個剪枝過程建立在固定不變的參數空間 上，本質上是一種被動的篩選機制。這進一步凸顯了以下深層衝突：

• 密集訓練 的本質是隱式地激勵模型充分利用每一個參數。每個參數都承載了一定的知識或推理能力，並通過參數間的協同工作共同支撐模型的整體表達能力。

• 稀疏推理 則要求模型僅基於被保留的部分參數完成推理任務，並保持高性能。

這種訓練目標與推理機制之間的內在不一致，意味着直接裁剪必然會導致部分知識或推理能力的丟失，從而破壞原有參數間協同工作的平衡，引發性能下降。

02 技術方案：DenoiseRotator------從"被動篩選"到"主動優化"的範式轉變

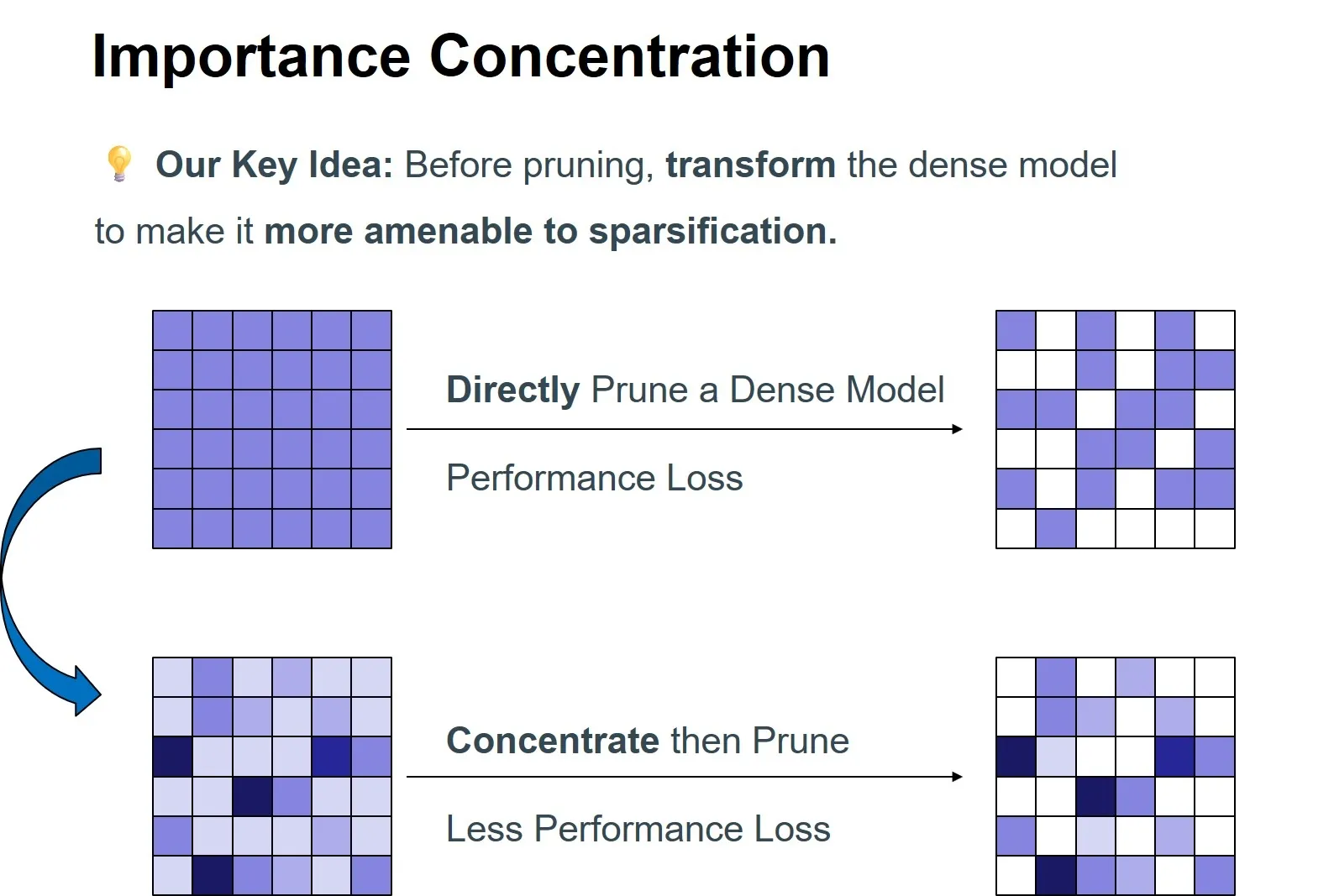
針對上述挑戰，我們重新思考剪枝範式：能否在剪枝前先對模型進行稀疏性引導的優化 ，使其自身結構更易於被剪枝 ？ 基於此，我們提出了"重要性濃縮"的全新思路，並開發了DenoiseRotator框架予以實現。

2.1 核心思想：重要性濃縮

我們的核心目標是在執行剪枝之前 ，將原本分散在眾多參數上的重要性，儘可能地集中到一個較小的參數子集中 。這樣，在後續剪枝過程中，被移除權重所包含的關鍵信息將大幅減少，從而顯著增強剪枝的魯棒性。 為量化並優化"濃縮"效果，我們引入了信息熵 作為衡量指標。通過將參數重要性分數歸一化為概率分佈，其熵值直接反映了重要性的集中程度：熵越低，表明重要性越集中於少數參數。因此，我們的優化目標明確為最小化歸一化重要性分佈的熵。

2.2 實現機制：可學習的正交變換

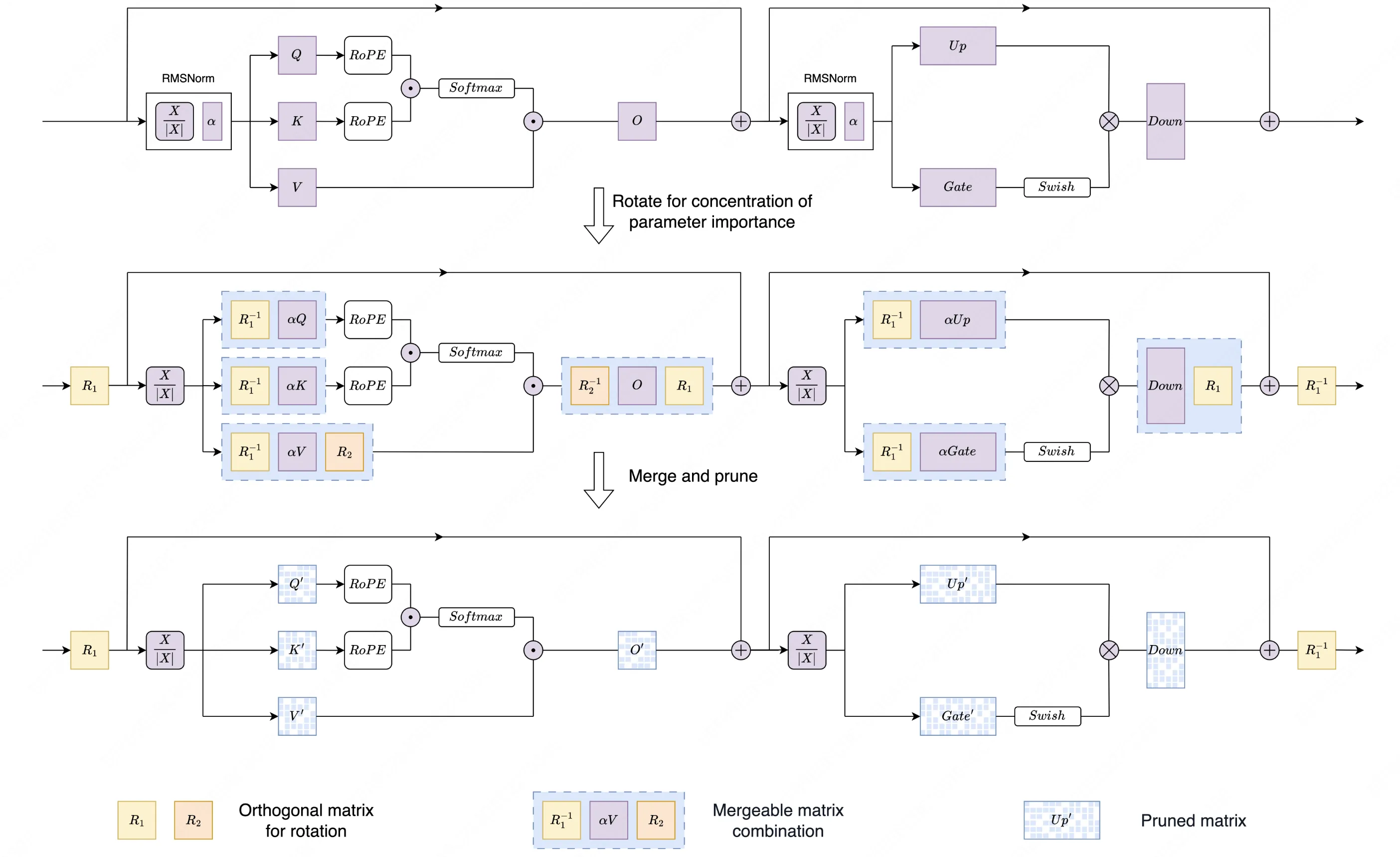
DenoiseRotator通過向Transformer層中引入可學習的正交矩陣，實現重要性分佈的熵減與濃縮。

如上圖所示，我們在Transformer層的特定位置（例如Attention模塊的Value和Output投影層前後）插入正交矩陣。這些矩陣對原始權重進行"旋轉"變換，在保持模型輸出完全不變（得益於正交變換的計算不變性）的前提下，重新分配參數的重要性。

2.3 關鍵優勢

訓練與剪枝解耦 ：DenoiseRotator採用模塊化設計 ，正交矩陣的優化與具體剪枝方法完全獨立。我們首先利用校準數據，以最小化重要性熵為目標訓練這些正交矩陣；訓練完成後，將其合併回原始權重。此時，我們獲得了一個"易於剪枝"的優化版稠密模型，可無縫對接任何現有剪枝工具（如SparseGPT、Wanda）進行後續操作。

優化過程穩定：正交變換具有保範數特性，確保在重新分佈重要性時，既不會人為引入也不會丟失總重要性量，從而保證了優化過程的穩定性，不影響原始模型性能。

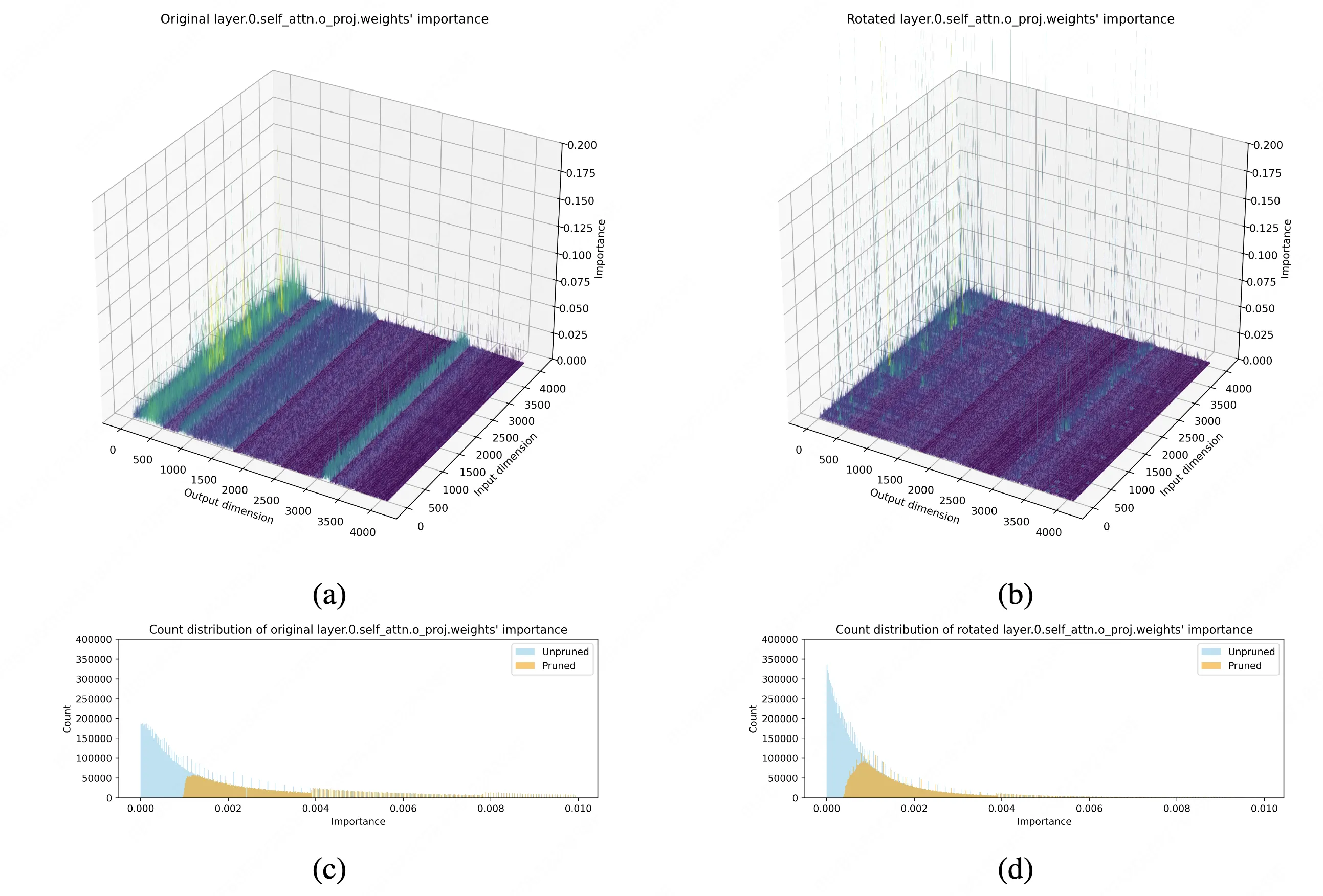
下圖直觀展示了DenoiseRotator的有效性。以LLaMA-3-8B模型首層輸出投影層為例，經我們的方法變換後，參數重要性分佈從分散趨於高度集中，為後續剪枝奠定了堅實基礎。

03 實驗驗證

在前文中，我們介紹了DenoiseRotator的核心思想------通過重要性濃縮提升剪枝魯棒性。那麼，這一方法在實際效果上表現如何？我們針對多個主流開源大模型進行了全面評測，涵蓋語言建模和零樣本推理任務，並與現有剪枝方法進行了對比。

3.1 實驗設置：覆蓋多模型、多任務、多剪枝方法

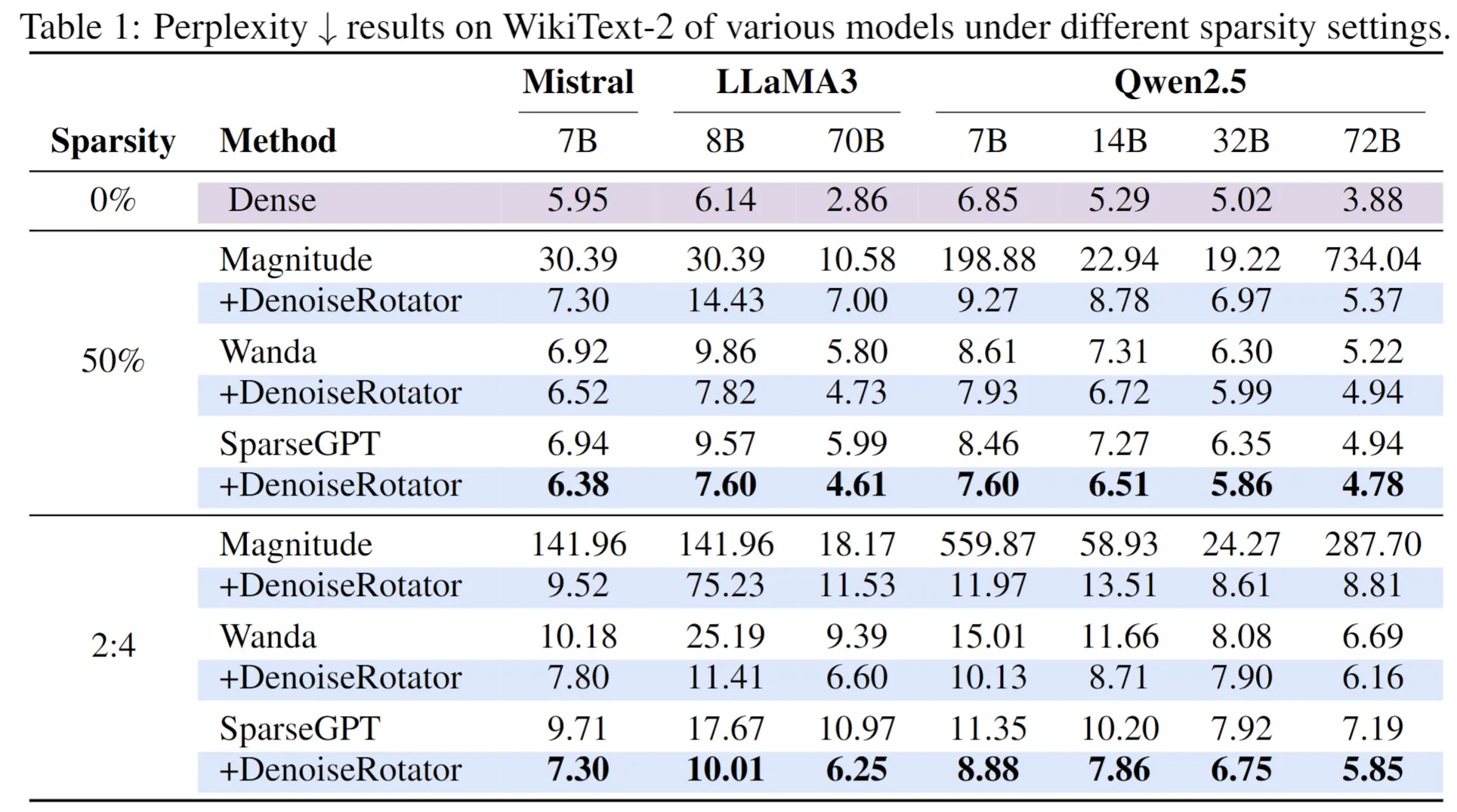
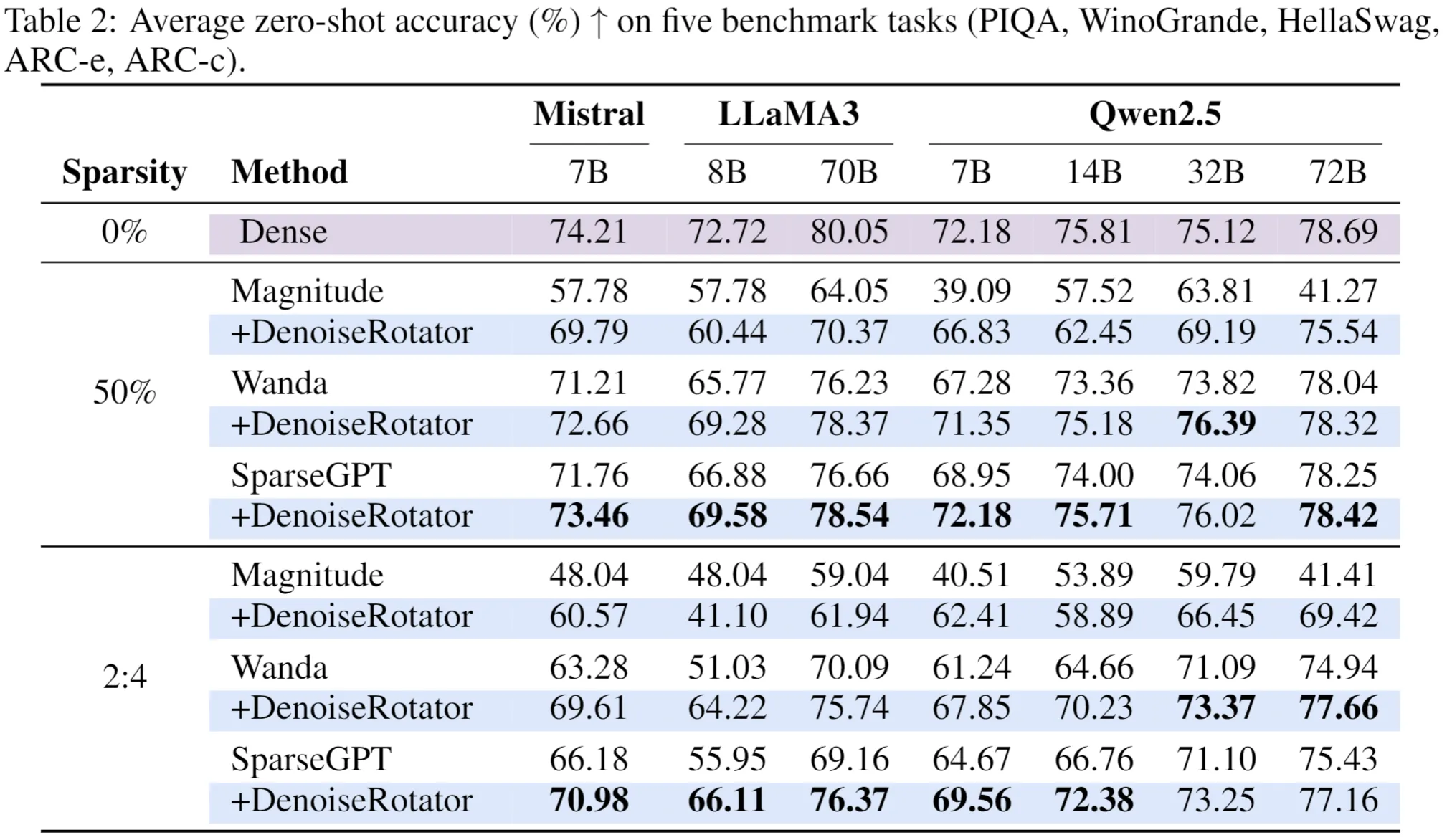
為全面評估DenoiseRotator的有效性，我們在多樣化的實驗設置下進行了系統性驗證。實驗覆蓋了從Mistral-7B、LLaMA3（8B/70B）到Qwen2.5（7B/14B/32B/72B）等多個主流開源大模型，評測任務包括語言建模（使用WikiText-2驗證集的困惑度PPL作為指標）和零樣本推理（在PIQA、WinoGrande、HellaSwag、ARC-e和ARC-c五個基準任務上評估平均準確率）。在基線方法方面，我們將DenoiseRotator與三類剪枝方法結合：經典方法Magnitude，以及先進方法Wanda和SparseGPT，並在非結構化（50%稀疏）和半結構化（2:4稀疏）兩種稀疏模式下進行對比評測。

3.2 主要結果：語言建模與零樣本推理全面提升

下表展示了不同模型在剪枝前後的困惑度（衡量語言建模能力）與零樣本任務表現。DenoiseRotator在所有模型和稀疏模式下均顯著降低剪枝造成的性能下降，尤其在2:4稀疏下提升更為明顯。

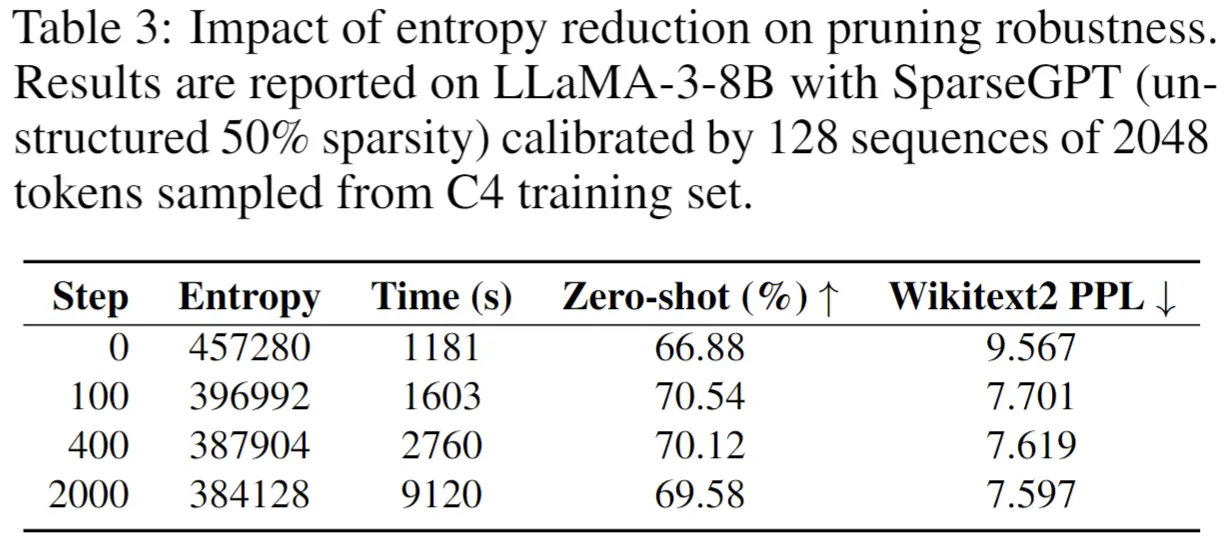
3.3 深入分析：熵減如何驅動剪枝魯棒性？

我們通過消融實驗驗證了重要性熵與剪枝效果的直接關聯。以LLaMA3-8B為例，記錄不同訓練步數下的熵值變化與模型性能：

熵減少13%（步數100）即可帶來零樣本任務準確率提升3.66%（66.88%➡70.54%），困惑度降低19.5%（9.567➡7.701）。進一步優化可繼續降低困惑度，驗證了重要性集中度與剪枝魯棒性的正相關。

3.4 部署效率：輕量開銷，顯著收益

• 參數增量：每層新增一個（hidden_size,hidden_size）正交矩陣。以LLaMA3-8B為例，總參數量增加約0.5B（佔原模型6.7%）。通過分塊對角矩陣（見論文附錄）可進一步降低開銷，適合資源受限場景。

• 推理耗時：單層Transformer的2:4稀疏計算耗時4.37ms，加入正交矩陣後僅增加0.32ms（1.24×加速比 vs 稠密層）。

04 總結

DenoiseRotator提出了一種創新的剪枝視角：將模型準備（重要性濃縮）與模型壓縮（剪枝）兩個階段解耦 。通過可學習的正交變換，主動實現參數重要性的濃縮，從而顯著提升後續剪枝的魯棒性。該方法具備即插即用的特性，為大規模語言模型的高效、高性能壓縮提供了新的技術路徑。

項目地址 ：https://github.com/Axel-gu/DenoiseRotator

希望跟大家一起學習交流。如果大家對這項工作感興趣，歡迎在GitHub上Star、Fork並參與討論！

| 關注「美團技術團隊」微信公眾號，在公眾號菜單欄對話框回覆【2024年貨】、【2023年貨】、【2022年貨】、【2021年貨】、【2020年貨】、【2019年貨】、【2018年貨】、【2017年貨】等關鍵詞，可查看美團技術團隊歷年技術文章合集。

| 本文系美團技術團隊出品，著作權歸屬美團。歡迎出於分享和交流等非商業目的轉載或使用本文內容，敬請註明"內容轉載自美團技術團隊"。本文未經許可，不得進行商業性轉載或者使用。任何商用行為，請發送郵件至 tech@meituan.com 申請授權。